【図解】多重共線性（VIF）とは？｜重回帰がうまくいかない原因

※本記事にはプロモーション（広告）が含まれています。

回帰分析の記事は、初心者が読む順に次の記事にまとめています。

あわせて読みたい

回帰分析の学習ロードマップ｜初心者が最短で使いこなす全記事ガイド

最短で使いこなす全記事ガイド

「重回帰分析をやってみたけど、結果がおかしい…」

そんな経験はありませんか？

たとえば、「広告費が増えると売上が増える」はずなのに、偏回帰係数がマイナスになっている。あるいは、明らかに重要な変数なのに、t検定で「有意でない」と判定されてしまう。

その原因、もしかすると「多重共線性」かもしれません。

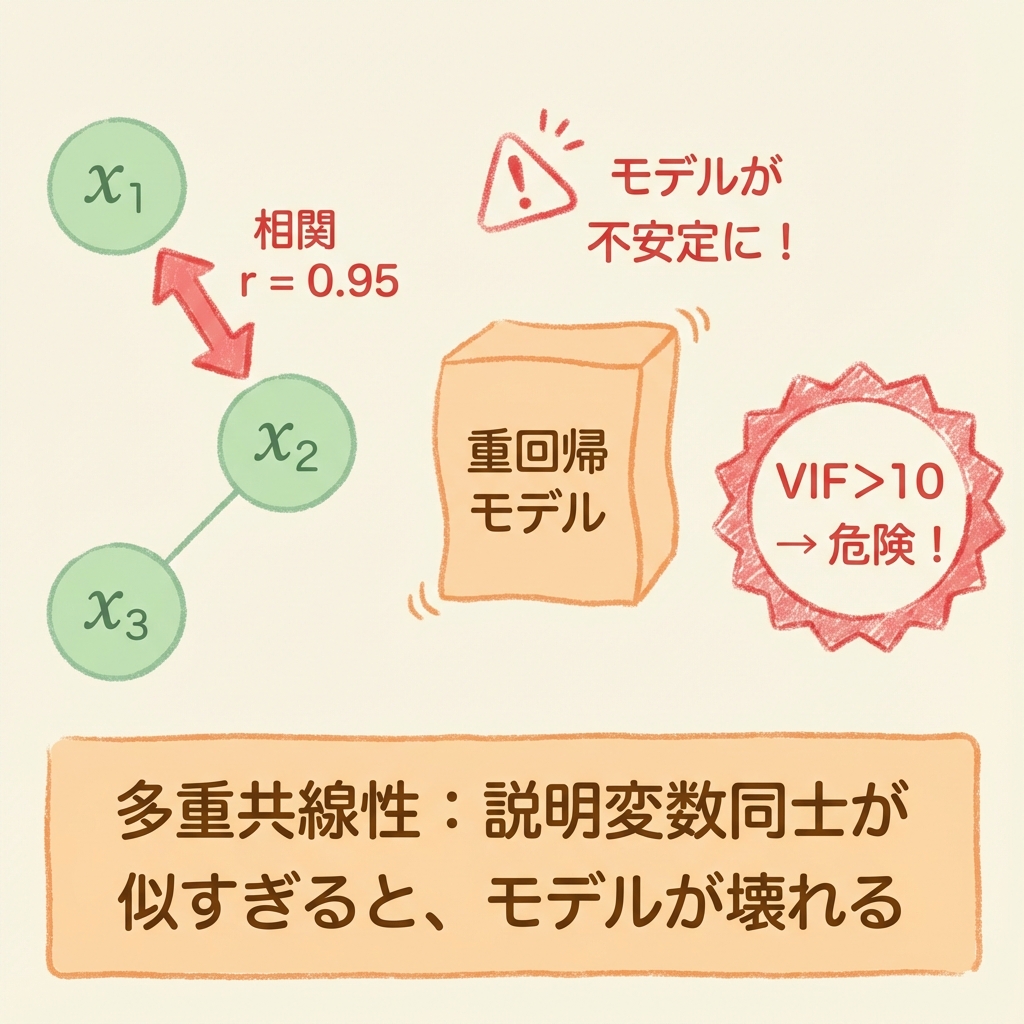
多重共線性とは、説明変数同士が強く相関している状態のこと。これが起きると、重回帰分析の結果が不安定になり、正しい解釈ができなくなってしまいます。

この記事では、多重共線性の仕組みから検出方法（VIF）、対処法まで、図解でわかりやすく解説します。

多重共線性とは？

説明変数同士が「似すぎている」状態

多重共線性（Multicollinearity）とは、説明変数同士が強く相関している状態のことです。

たとえば、売上を予測するモデルで「広告費」と「マーケティング費」を両方入れたとします。

でも、よく考えてみてください。広告費とマーケティング費って、ほとんど同じものですよね。広告費が多い月はマーケティング費も多いし、少ない月は両方少ない。

このように、2つの変数が「似すぎている」と、重回帰分析はうまく機能しなくなります。

「双子」で考えるとわかりやすい

多重共線性のイメージを、双子の例で考えてみましょう。

あなたは「チームの売上」を予測したいと思っています。チームには太郎さんと次郎さんがいます。

ところが、太郎さんと次郎さんは一卵性双生児で、行動パターンがまったく同じ。太郎さんが頑張る日は次郎さんも頑張るし、太郎さんがサボる日は次郎さんもサボる。

この状態で、「売上への貢献は太郎さんのおかげ？次郎さんのおかげ？」と聞かれたら、答えられますか？

…答えられませんよね。2人の行動が似すぎていて、どちらの効果か区別できないからです。

説明変数どうしが一緒に動く「相関」は、原因と結果の「因果」とは別ものです。この違いは次の記事でたとえを使って解説しています。

あわせて読みたい

疑似相関（擬似相関）とは？因果関係との違いと見抜き方を例で図解

「擬似相関」の罠を例で解説

多重共線性があると何が起こる？

問題①：偏回帰係数が不安定になる

多重共線性があると、偏回帰係数がサンプルごとに大きく変動します。

たとえば、あるサンプルで計算すると b₁ = 5.0 だったのに、別のサンプルでは b₁ = −2.0 になる、ということが起こります。

これは、x₁とx₂が似すぎているため、「x₁の効果」と「x₂の効果」の配分がサンプルによってコロコロ変わってしまうからです。

問題②：標準誤差が大きくなる

偏回帰係数が不安定ということは、標準誤差が大きくなるということです。

標準誤差が大きくなると、t値（= 係数 ÷ 標準誤差）が小さくなります。

その結果、本当は効いている変数なのに「有意でない」と判定されてしまうことがあります。

状態	標準誤差	t値	判定
多重共線性なし	小さい	大きい	有意になりやすい
多重共線性あり	大きい	小さい	有意にならない

問題③：符号が逆転することがある

最も厄介なのが、偏回帰係数の符号が理論と逆になることです。

「広告費を増やすと売上が増える」のが常識なのに、偏回帰係数がマイナスになっている…。これは多重共線性の典型的な症状です。

なぜこんなことが起こるのでしょうか？

偏回帰係数は「他の変数を固定したときの効果」を表します。でも、x₁とx₂が強く相関していると、「x₁だけ変えてx₂を固定する」という状況が現実にはほとんど存在しないのです。

存在しない状況を無理やり推定するので、結果が不自然になってしまいます。

VIF（分散拡大係数）で多重共線性を検出する

VIFとは？｜「分散がどれだけ膨らんだか」を測る指標

多重共線性を検出する最もポピュラーな指標がVIF（Variance Inflation Factor：分散拡大係数）です。

VIFは、「他の説明変数との相関によって、偏回帰係数の分散がどれだけ膨らんだか」を表す指標です。

VIFが大きいほど、その変数は他の変数と強く相関しており、偏回帰係数の推定が不安定になっています。

VIFの計算式

VIFは、各説明変数について計算します。

ちょっとわかりにくいので、具体的に説明しますね。

たとえば、x₁のVIFを計算したいとします。このとき、次のような回帰分析を行います。

つまり、「x₁が他の説明変数（x₂, x₃）でどれだけ説明できるか」を調べているのです。

もしx₁がx₂やx₃で完全に説明できる（R₁² = 1）なら、VIF = 1 ÷ 0 = ∞ となり、多重共線性は完全に発生しています。

VIFの判定基準

VIFの判定基準は、一般的に以下のように言われています。

VIFの値	判定	対応
VIF < 5	問題なし	そのまま分析を続けてOK
5 ≦ VIF < 10	要注意	多重共線性の可能性あり。結果の解釈に注意
VIF ≧ 10	深刻な問題	多重共線性あり。対処が必要

ソフトによっては VIF の代わりに許容度（トレランス）＝1−R²＝1÷VIF を表示します。許容度 0.1 が VIF 10、許容度 0.2 が VIF 5 にあたります。5と10はどちらも経験からの目安で、分野や本によって基準が違います。

あわせて読みたい

回帰診断とは？残差プロットとVIFで回帰式の健康チェック

回帰診断とは？残差プロットとVIFで回帰式の健康チェック

【計算例】VIFを実際に求めてみよう

問題設定：3つの説明変数があるモデル

売上（y）を「広告費（x₁）」「マーケティング費（x₂）」「店舗面積（x₃）」で予測するモデルを考えます。

各説明変数を目的変数として、他の変数で回帰分析した結果、以下の決定係数が得られました。

VIFの計算

広告費（x₁）のVIF

マーケティング費（x₂）のVIF

店舗面積（x₃）のVIF

結果のまとめと判定

変数	Rⱼ²	VIF	判定
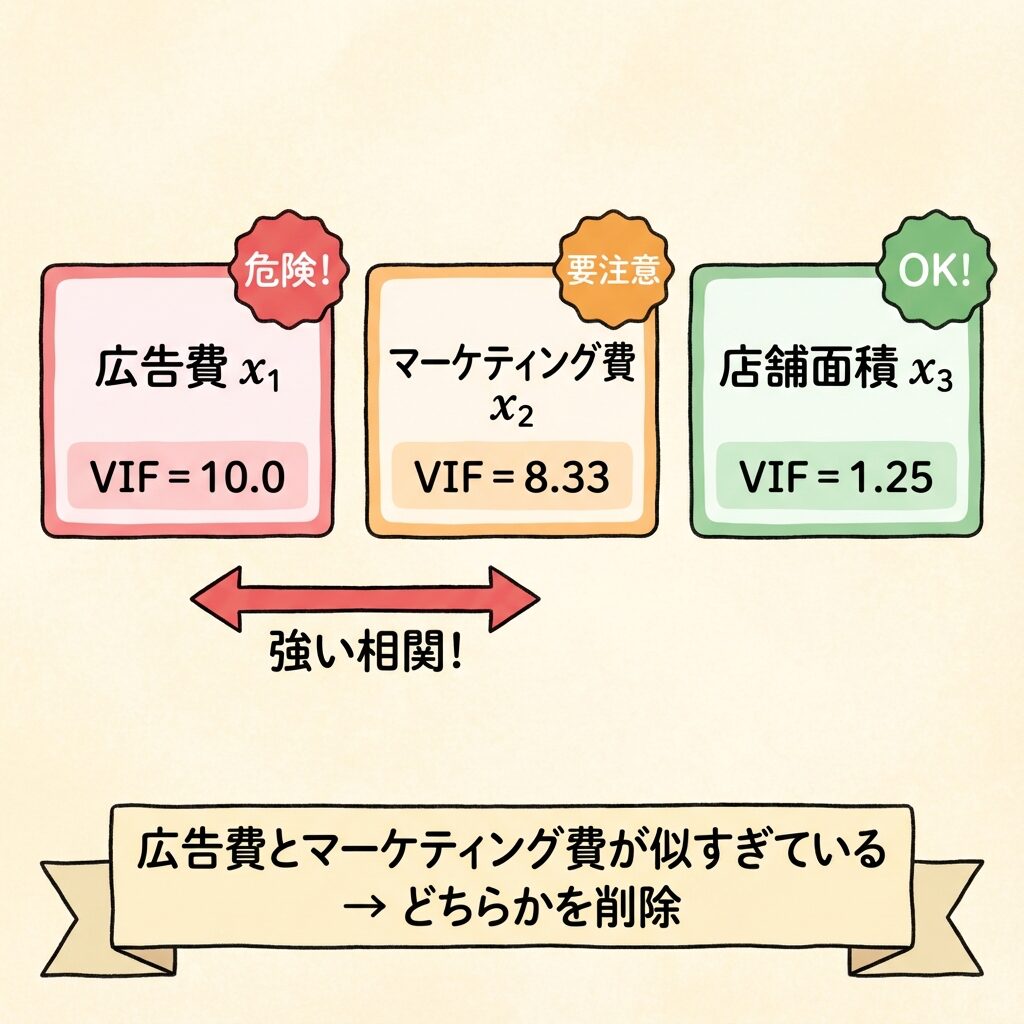
広告費 x₁	0.90	10.0	危険
マーケティング費 x₂	0.88	8.33	要注意
店舗面積 x₃	0.20	1.25	問題なし

VIF の大きい変数をどう外すかは、変数選択の方法(ステップワイズ法など)で決めます。

あわせて読みたい

変数選択の方法｜ステップワイズ法・AIC・増加法・減少法

ステップワイズ法・AIC・増加法・減少法

多重共線性への対処法

対処法①：変数を削除する（最もシンプル）

最もシンプルな対処法は、相関の高い変数のどちらかを削除することです。

先ほどの例なら、「広告費」と「マーケティング費」のどちらかを削除します。どちらを残すかは、以下の観点で判断します。

• 理論的に重要な方を残す
• 測定精度が高い方を残す
• データの欠損が少ない方を残す

対処法②：変数を統合する

相関の高い変数を1つの変数に統合する方法もあります。

先ほどの例なら、「広告費」と「マーケティング費」を足して「プロモーション費」という1つの変数にします。

この方法なら、情報を捨てずに多重共線性を解消できます。ただし、「広告費」と「マーケティング費」の個別の効果はわからなくなります。

対処法③：主成分分析を使う

より高度な方法として、主成分分析（PCA）を使う方法があります。

主成分分析は、相関のある変数から「相関のない新しい変数（主成分）」を作り出す手法です。この主成分を説明変数として使えば、多重共線性は発生しません。

ただし、主成分は元の変数の「合成」なので、解釈が難しくなるというデメリットがあります。

対処法④：サンプルサイズを増やす

サンプルサイズを増やすと、標準誤差が小さくなり、多重共線性の影響を軽減できます。

ただし、これは「根本的な解決」ではなく「影響を和らげる」だけです。VIFが非常に高い場合（10以上）は、サンプルを増やしても問題が残ることがあります。

対処法のまとめ

対処法	メリット	デメリット
①変数を削除	シンプル、確実	情報が失われる
②変数を統合	情報を保持できる	個別の効果がわからない
③主成分分析	多くの変数に対応可	解釈が難しくなる
④サンプル増加	変数を変えなくてよい	根本的解決ではない

多重共線性チェックの流れ

まとめ

この記事では、多重共線性とVIFについて解説しました。

多重共線性は、重回帰分析の「落とし穴」です。分析前にVIFをチェックする習慣をつけましょう。

次は、「どの変数をモデルに入れるべきか」を決める変数選択の方法について学びましょう。

よくある質問