- V(XY)の公式、なんでこんなに複雑なの?
- 「和」の分散と「積」の分散、何が違うの?
- E(Y)²とかE(X)²が出てくる理由がわからない…
- QC検定1級の計算問題で、どこから手をつければいいかわからない
- 確率変数の「積」E(XY)とV(XY)の公式
- なぜV(XY)が「3つの項」の和になるのか、直感的な理由
- 「和」と「積」の公式の違いを一発で理解する比較表
- QC検定1級レベルの計算問題をStep by Stepで攻略
QC検定1級や統計検定を勉強していると、こんな公式に出会いませんか?
※ XとYが独立な場合
「え、なにこれ?」「和の分散はV(X)+V(Y)でシンプルだったのに…」
そう思いますよね。私も最初は全く理解できませんでした。
でも、この公式には「ちゃんとした理由」があります。
この記事では、「なぜこんな複雑な式になるのか」をイメージで徹底解説します。丸暗記ではなく、「なるほど、だからこうなるのか」と腑に落ちる説明を目指します。
第9回:分散の加法性|「独立」なら足せる!バラつきの合成法則を徹底解説 →
目次
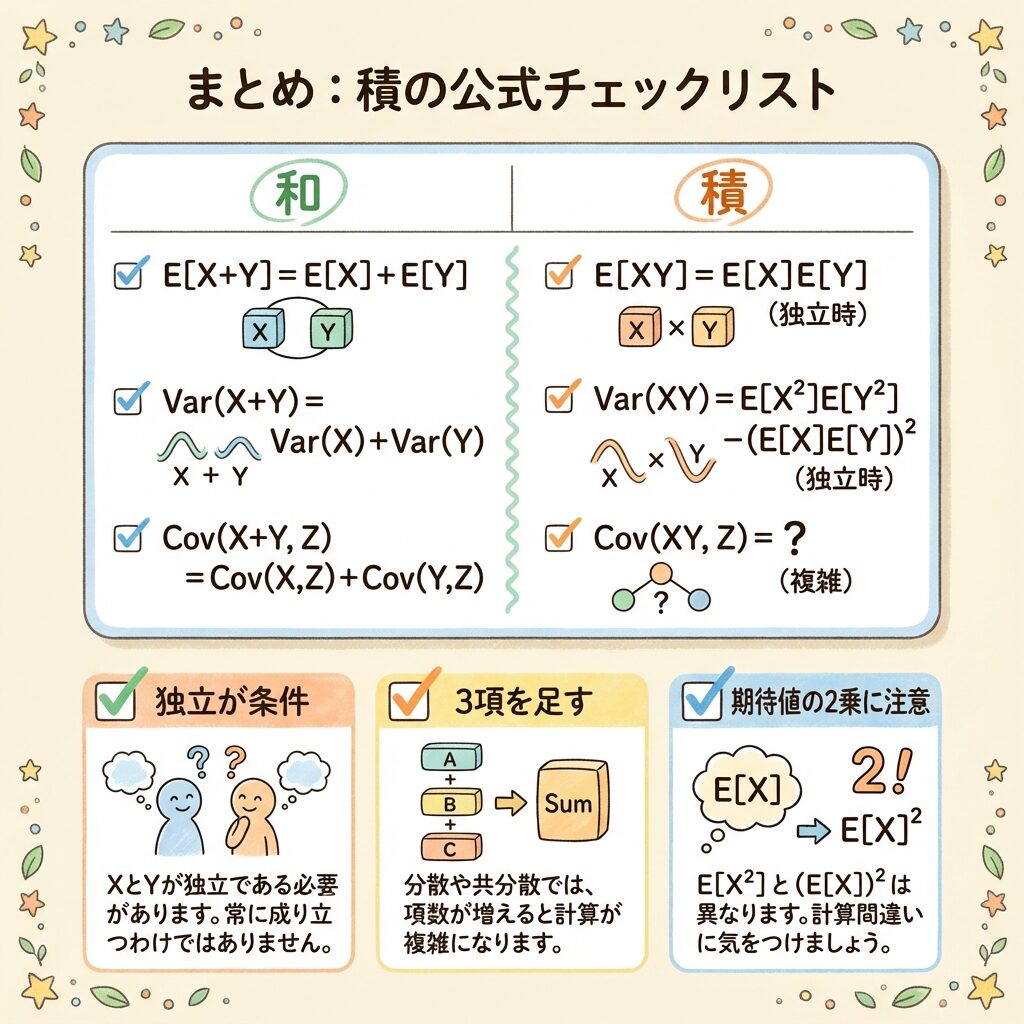
🎯 まず結論:「和」と「積」の公式を比較しよう
最初に、「和」と「積」の公式の違いを明確にしましょう。
これを頭に入れておくと、「なぜ積は複雑なのか」がわかりやすくなります。
| 項目 | 和 X + Y | 積 XY |
|---|---|---|
| 期待値 | E(X+Y) = E(X) + E(Y) 常に成立 |
E(XY) = E(X) × E(Y) 独立のみ成立 |
| 分散 (独立時) |
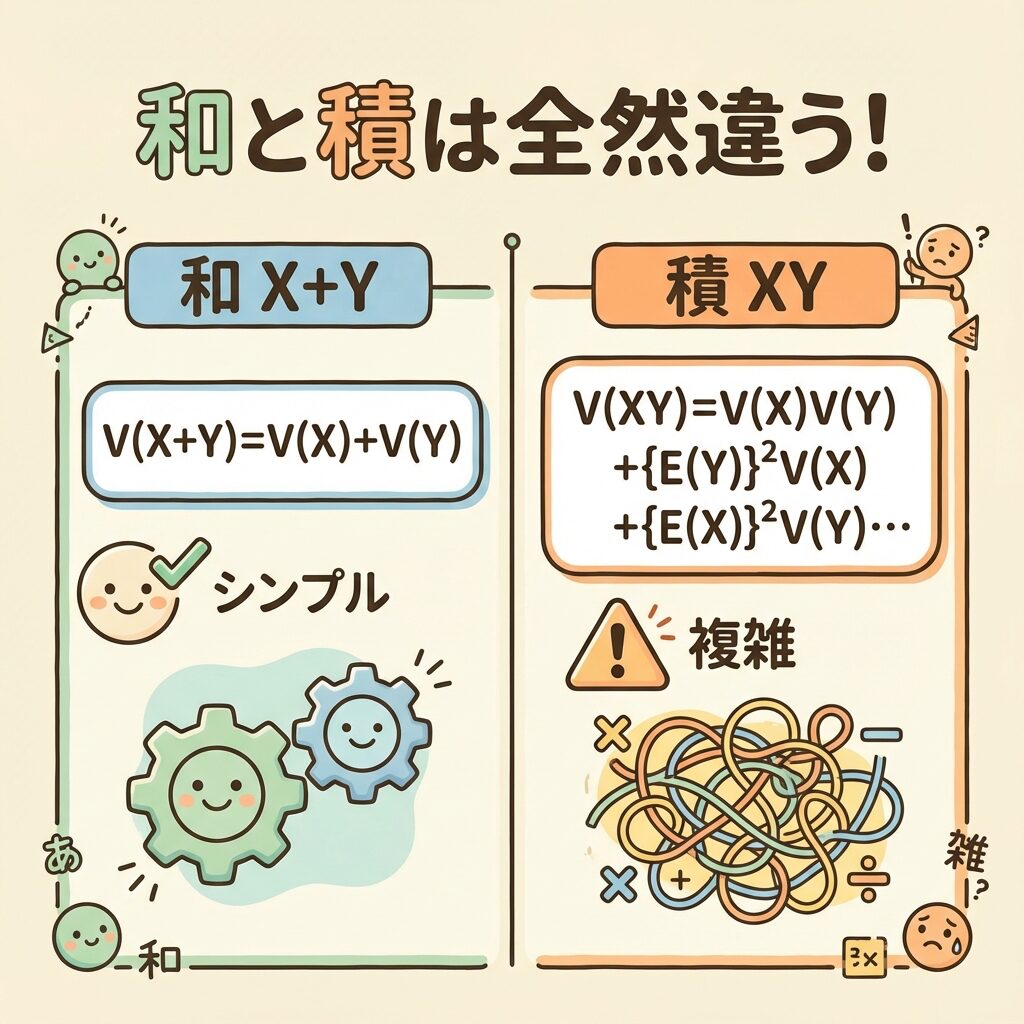
V(X+Y) = V(X) + V(Y) ✓ シンプル! |
V(XY) = V(X)V(Y) + {E(Y)}²V(X) + {E(X)}²V(Y) ⚠️ 3項ある! |
| 計算の複雑さ | ★☆☆ 足すだけ |
★★★ 期待値の2乗も使う |
ポイントは、「積」の分散には3つの項があること。
なぜ3つなのか?それを次のセクションで解説します。
🧮 期待値の積:E(XY) = E(X) × E(Y)
まず、期待値(平均)から見ていきましょう。こちらは比較的シンプルです。
独立なら「期待値の積」=「積の期待値」
XとYが独立なら、以下の公式が成り立ちます。
※ XとYが独立な場合のみ成立
これは直感的に理解しやすいですね。
🎯 たとえ話:サイコロ2個の積
サイコロを2個振って、出た目を掛け算する場合を考えましょう。
- サイコロXの期待値:E(X) = 3.5
- サイコロYの期待値:E(Y) = 3.5
- XとYは独立(一方の出目が他方に影響しない)
このとき、積XYの期待値は:
E(XY) = E(X) × E(Y) = 3.5 × 3.5 = 12.25
「平均的に、積は12.25くらいになる」ということです。
XとYが独立でない(相関がある)場合は、E(XY) ≠ E(X)×E(Y) となります。
この場合は E(XY) = E(X)E(Y) + Cov(X,Y) という式を使います。
📊 分散の積:なぜ「3つの項」になるのか?
さて、ここからが本題です。
V(XY)はなぜ複雑な式になるのか?を、イメージで理解していきましょう。
V(XY)の公式を分解して理解する
V(XY)の公式をもう一度見てみましょう。
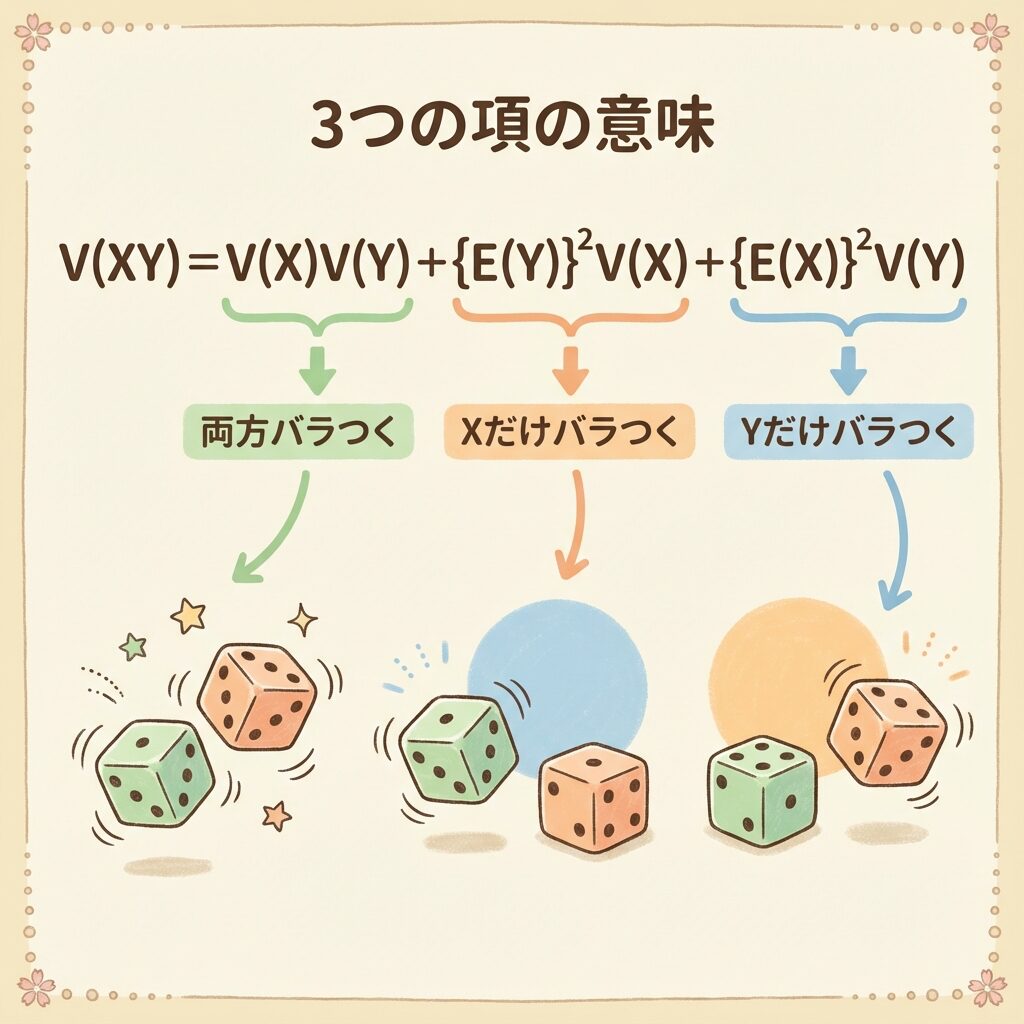
この3つの項、それぞれに「意味」があります。
| 項 | 式 | 意味(イメージ) |
|---|---|---|
| 第1項 | V(X)V(Y) | XもYも両方バラつくことによる影響 |
| 第2項 | {E(Y)}²V(X) | Yは平均で固定、Xだけバラつくことによる影響 |
| 第3項 | {E(X)}²V(Y) | Xは平均で固定、Yだけバラつくことによる影響 |
🏭 たとえ話:長方形の面積で考える
「積のバラつき」を理解するために、長方形の面積で考えてみましょう。
長方形の面積 = 縦 × 横 です。
- 縦の長さ X:平均 E(X)、バラつき V(X)
- 横の長さ Y:平均 E(Y)、バラつき V(Y)
- 面積 XY:そのバラつき V(XY) は?
面積のバラつきには、3つの「源泉」があります。
① 縦も横も両方バラつく → 面積のバラつきに影響
② 横が平均的な長さのとき、縦だけバラつく → 面積のバラつきに影響
③ 縦が平均的な長さのとき、横だけバラつく → 面積のバラつきに影響
この3つを合計したものが、V(XY)なのです。
【QC検定1級】確率変数の和の平均・分散・共分散|部品組立問題を完全攻略 →
📝 V(XY)の公式を数学的に導出する
イメージで理解したところで、次は数学的な導出を見てみましょう。
「なぜこの式になるのか」を論理的に追うことで、より深い理解が得られます。
導出のステップ
Step 1:分散の定義を思い出す
分散の定義は「期待値からのズレの2乗の期待値」です。
この公式を使って、V(XY)を展開していきます。
Step 2:E[(XY)²]を計算する
XとYが独立なので、(XY)² = X²Y² も独立な変数の積です。
独立なら E[X²Y²] = E[X²] × E[Y²] が成り立つので:
E[(XY)²] = E[X²] × E[Y²]
Step 3:E[X²]を分散で表す
ここで、重要な変形を使います。
分散の定義 V(X) = E[X²] − {E(X)}² を変形すると:
「2乗の期待値」=「分散」+「期待値の2乗」
同様に E[Y²] = V(Y) + {E(Y)}² です。
Step 4:代入して展開する
Step 2の式に代入します。
E[(XY)²] = E[X²] × E[Y²]
= {V(X) + E(X)²} × {V(Y) + E(Y)²}
= V(X)V(Y) + V(X)E(Y)² + E(X)²V(Y) + E(X)²E(Y)²
Step 5:{E(XY)}²を計算する
独立なので E(XY) = E(X)E(Y) より:
{E(XY)}² = {E(X)E(Y)}² = E(X)²E(Y)²
Step 6:分散の公式に代入
V(XY) = E[(XY)²] − {E(XY)}² に代入すると:
V(XY) = {V(X)V(Y) + V(X)E(Y)² + E(X)²V(Y) + E(X)²E(Y)²} − E(X)²E(Y)²
赤字の部分が打ち消し合って:
① 分散の定義 V(XY) = E[(XY)²] − {E(XY)}² を使う
② 独立なら E[X²Y²] = E[X²]E[Y²] が使える
③ E[X²] = V(X) + {E(X)}² の変形がカギ
④ 展開すると E(X)²E(Y)² が打ち消し合う
第5回:分散と標準偏差|「バラつき」を数値化する魔法の公式 →

✏️ 例題で完全マスター|QC検定1級レベル
実際の問題を解いて、公式の使い方を身につけましょう。
例題:製品の総出荷量を計算せよ
ある製品の「1個あたりの長さ X」と「1日の生産数 Y」は互いに独立で、以下の統計量を持つ。
| 変数 | 期待値 E | 分散 V |
|---|---|---|
| 長さ X | E(X) = 10.0 cm | V(X) = 0.01 cm² |
| 生産数 Y | E(Y) = 0.5 万個/日 | V(Y) = 0.12 (万個/日)² |
問1:総出荷量 XY の期待値 E(XY) を求めよ。
問2:総出荷量 XY の分散 V(XY) を求めよ。
問3:総出荷量 XY の標準偏差 σ(XY) を求めよ。
解答:Step by Step
問1:E(XY)の計算
XとYは独立なので、期待値の積の公式が使えます。
E(XY) = E(X) × E(Y)
= 10.0 × 0.5
= 5.0 (cm・万個/日)
問2:V(XY)の計算
V(XY)の公式に代入します。
V(XY) = V(X)V(Y) + {E(Y)}²V(X) + {E(X)}²V(Y)
各項を計算します。
| 項 | 計算 | 結果 |
|---|---|---|
| 第1項 | V(X)×V(Y) = 0.01 × 0.12 | 0.0012 |
| 第2項 | {E(Y)}²×V(X) = 0.5² × 0.01 = 0.25 × 0.01 | 0.0025 |
| 第3項 | {E(X)}²×V(Y) = 10.0² × 0.12 = 100 × 0.12 | 12.0 |
V(XY) = 0.0012 + 0.0025 + 12.0
≒ 12.0 または 約12
第3項 {E(X)}²V(Y) が圧倒的に大きいですね。これは「Xの期待値が大きい」ことが原因です。期待値が大きい方の2乗は、分散への影響が大きくなります。
問3:σ(XY)の計算
σ(XY) = √V(XY)
= √12.0
≒ 3.46
共分散とは?|「気温が上がるとビールが売れる」を数値化する方法 →
📚 まとめ|確率変数の「積」の公式
最後に、この記事のポイントを整理しましょう。
- 期待値の積:E(XY) = E(X) × E(Y)(独立なら成立)
- 分散の積:V(XY) = V(X)V(Y) + {E(Y)}²V(X) + {E(X)}²V(Y)
- V(XY)の3つの項は「両方バラつく」「Xだけ」「Yだけ」の影響
- 期待値が大きい方の2乗が、分散に大きく影響する
- 「和」の分散 V(X+Y) = V(X)+V(Y) とは全く異なる
📋 公式一覧(保存版)
| 公式名 | 公式 | 条件 |
|---|---|---|
| 期待値の積 | E(XY) = E(X) × E(Y) | 独立のみ |
| 分散の積 | V(XY) = V(X)V(Y) + {E(Y)}²V(X) + {E(X)}²V(Y) | 独立のみ |
| E[X²]の変形 | E[X²] = V(X) + {E(X)}² | 常に成立 |
🔑 QC検定1級での出題ポイント
- 「独立」の確認:問題文で独立かどうかを必ずチェック
- 3項の計算:一つずつ計算し、最後に足し合わせる
- 期待値の2乗:{E(X)}² と V(X) を混同しないこと
- 単位の確認:分散の単位は「元の単位の2乗」
① V(XY) = V(X) × V(Y) と計算してしまう({E(Y)}²V(X)などを忘れる)
② E(X)² を E(X²) と混同する
③ 独立でない場合に公式をそのまま使う
📖 次に読むべき記事
「和」の分散 V(X+Y) = V(X) + V(Y) を図解。「積」との違いが明確になります。
相関がある場合の分散の計算方法。QC検定1級の頻出テーマです。
共分散と相関係数の関係を図解。独立でない場合の計算に必須の知識です。
🔗 統計学基礎シリーズ
📊 QC検定・統計学の記事をもっと読む
統計学・QC検定 記事一覧へ →