- 実験計画法の手法が多すぎて、どれを使えばいいかわからない
- 乱塊法と分割法の違いがごっちゃになる
- 擬水準法と多水準法、名前が似ていて混乱する
- 直交表はいつ使うのか、基本の配置実験と何が違うのか不明
- 実験計画法の全体像と各手法の位置づけ
- 「この状況ならこの手法」がわかるフローチャート
- 混同しやすい手法の決定的な違い
- 各手法の詳細記事へのリンク集
目次
まず全体像を把握しよう:実験計画法の「地図」
実験計画法には多くの手法がありますが、実は「なぜその手法が必要か」という視点で整理すると、スッキリ理解できます。
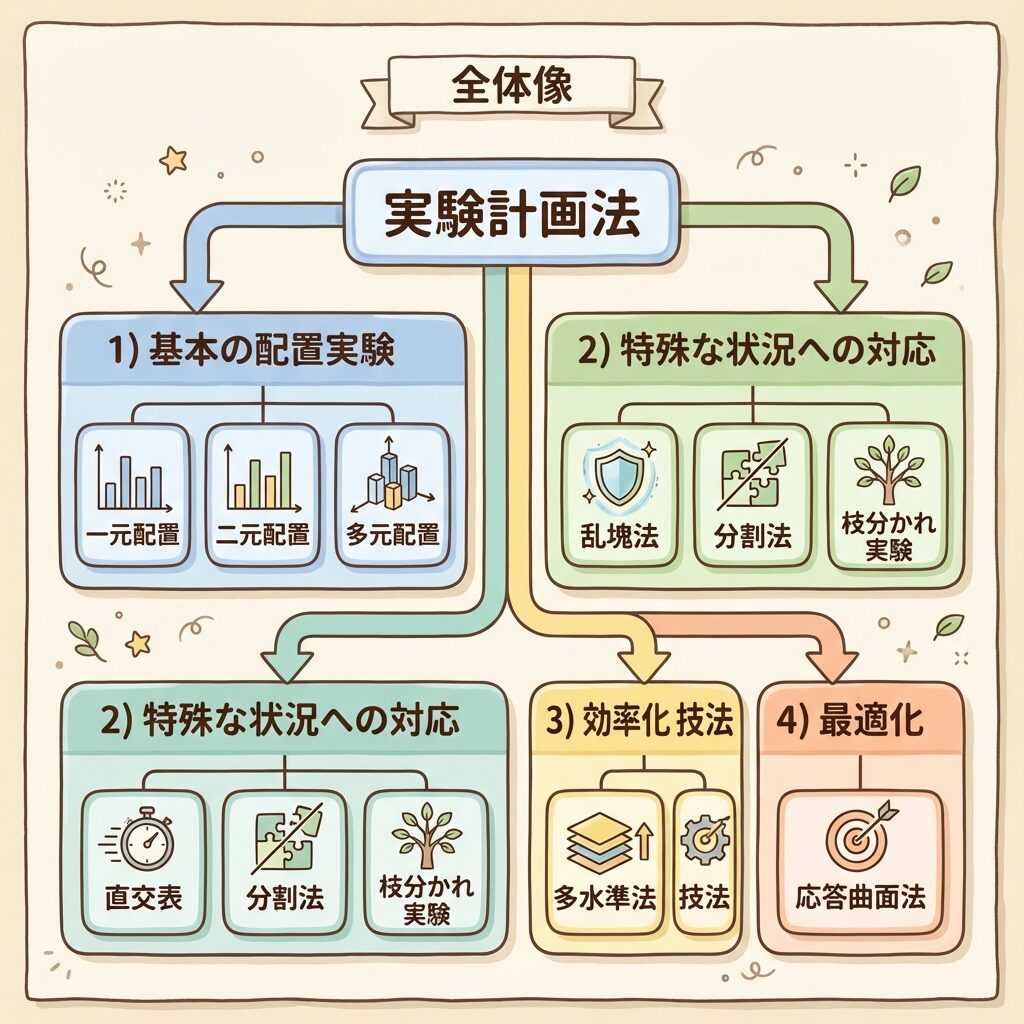
大きく分けると、以下の4つのカテゴリに分類できます。
| カテゴリ | 目的 | 含まれる手法 |
|---|---|---|
| ①基本の配置実験 | 因子の効果を調べる (基本形) |
一元配置、二元配置、多元配置 |
| ②特殊な状況への対応 | 現実の制約に対処する | 乱塊法、分割法、枝分かれ実験 |
| ③効率化の技法 | 実験回数を減らす | 直交表、擬水準法、多水準法 |
| ④最適化 | 最適な条件を探す | 応答曲面法 |
「この手法は何のために存在するのか?」を意識すると、手法選びで迷わなくなります。
・基本形で対応できる? → ①を使う
・現実に制約がある? → ②を使う
・実験回数が多すぎる? → ③を使う
・最適値を見つけたい? → ④を使う
カテゴリ①:基本の配置実験(まずはここから)
実験計画法の基本形です。「調べたい因子が何個あるか」で使い分けます。
📊 一元配置実験:因子が1つだけ
使う場面:「この1つの因子が効果あるか?」を調べたいとき
例:肥料の種類(A, B, C)だけを変えて、収穫量を比較する
特徴:最もシンプル。因子の効果と誤差だけを分離する
一元配置実験とは?1つの因子で白黒つける実験の基本形 →
📊 二元配置実験:因子が2つ
使う場面:「2つの因子の効果と、その組合せ効果(交互作用)」を調べたいとき
例:肥料の種類(A, B)と水やり頻度(多, 少)の両方を変えて比較
特徴:交互作用が検出できる(繰返しありの場合)
📊 多元配置実験:因子が3つ以上
使う場面:「3つ以上の因子を同時に検討したい」とき
問題点:因子が増えると実験回数が爆発的に増加する
例:3因子×2水準×2水準×3水準 = 12通り × 繰返し = 大量の実験…
因子が3つ以上になると、すべての組合せを実験する「完全実施」は現実的でないことが多いです。
→ この問題を解決するのが「直交表」です(後述)
カテゴリ②:特殊な状況への対応
現実の実験では、「環境にバラつきがある」「因子の変更が難しい」などの制約があります。それに対応する手法がこのカテゴリです。
ここが最も混乱しやすいポイントなので、丁寧に解説します。
【最重要】乱塊法 vs 分割法:決定的な違い
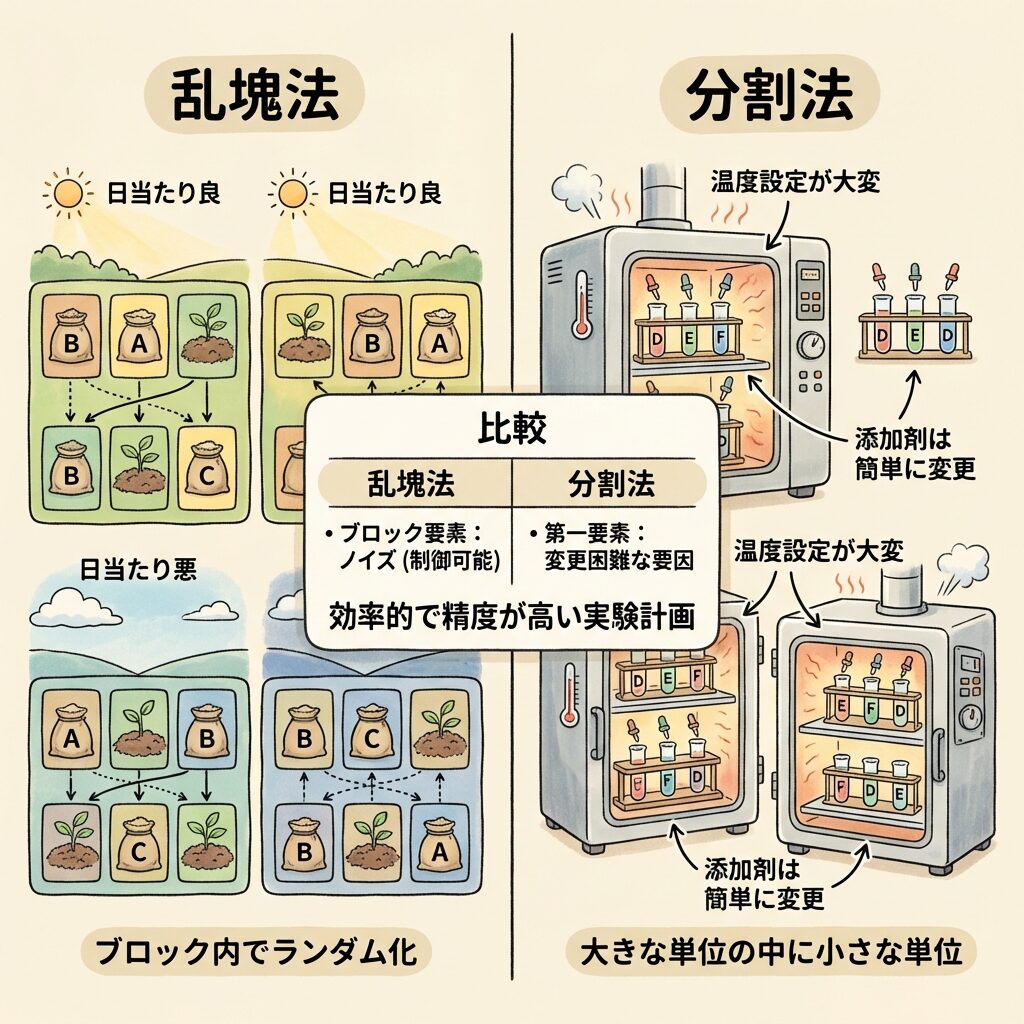
この2つは名前も似ていて、どちらも「ブロック」や「単位」という概念が出てくるため、混同しやすいです。しかし、「解決したい問題」がまったく違います。
🌾 乱塊法:「環境のバラつき」を取り除きたい
🎯 解決したい問題
「実験環境にバラつきがあり、それが結果に影響しそう」
具体例:
畑で肥料の効果を調べたいが、畑の日当たりが場所によって違う。日当たりの良い場所と悪い場所で結果が変わってしまう…
解決策:
「日当たり良好エリア」「日当たり不良エリア」をブロックとして分け、各ブロック内ですべての肥料を試す。これで日当たりの影響を統計的に除去できる。
・環境差、ロット差、日間差、機械差などの「ノイズを除去」したい
・ブロック内ではすべての水準を完全にランダム化して実験
・ブロック因子は「効果を調べたい因子」ではなく「邪魔な因子」
乱塊法とは?実験条件にばらつきがあるときの設計法 →
🏭 分割法:「変更が難しい因子」がある
🎯 解決したい問題
「ある因子の水準変更に時間やコストがかかり、頻繁に変えられない」
具体例:
焼成炉の温度変更に2時間かかる。温度(A)と添加剤(B)の効果を調べたいが、温度を頻繁に変えるのは非効率…
解決策:
温度を1次因子として「まとめて設定」し、その温度のまま添加剤(2次因子)だけをランダムに変えて実験。温度変更は最小限に。
・因子の水準変更に時間・コストがかかる
・1次単位(大)の中に2次単位(小)がある入れ子構造
・誤差が2種類(1次誤差と2次誤差)ある
・すべての因子の効果を調べたい(邪魔な因子ではない)
分割法とは?複雑な条件を整理するための実験設計 →
📊 乱塊法 vs 分割法:比較表
| 比較項目 | 乱塊法 | 分割法 |
|---|---|---|
| 解決したい問題 | 環境のバラつきを除きたい | 変更困難な因子がある |
| ブロック/単位の扱い | ノイズ(邪魔な因子) | 調べたい因子の1つ |
| ランダム化 | ブロック内で完全ランダム化 | 制限付きランダム化 |
| 誤差の数 | 1つ | 2つ(1次・2次) |
| 典型的なキーワード | 日当たり、ロット、日間変動 | 温度変更に時間がかかる |
「その因子の効果を調べたいか?」を考える
・調べたくない(ノイズとして除去したい)→ 乱塊法
・調べたい(でも変更が大変)→ 分割法
🌿 枝分かれ実験(Nested Design):因子が「入れ子」になっている
🎯 解決したい問題
「ある因子の水準が、別の因子の中に入れ子(ネスト)になっている」
具体例:
3つの工場(A, B, C)があり、各工場に3人ずつ作業者がいる。工場Aの作業者1と工場Bの作業者1は別人。作業者は工場の中に「入れ子」になっている。
特徴:
分割法と似ているが、「交互作用」が意味を持たない(作業者は工場をまたがない)
カテゴリ③:効率化の技法(直交表と水準操作)
因子が多くなると、すべての組合せを実験する「完全実施」は現実的ではありません。そこで登場するのが「直交表」と「水準操作の技法」です。
📋 直交表:実験回数を劇的に減らす魔法の表
🎯 解決したい問題
「因子が多すぎて、すべての組合せを試すと実験回数が膨大になる」
具体例:
7因子×2水準 = 128通り。繰返し3回で384回の実験…無理!
解決策:
L8直交表を使えば、8回の実験で7因子の主効果がすべて評価できる!
【重要】擬水準法 vs 多水準法:名前は似てるが目的が違う
どちらも「直交表の水準数と、調べたい因子の水準数が合わないとき」に使う技法ですが、解決する問題が正反対です。
🔻 擬水準法(ダミー水準法):水準が「足りない」ときに使う
🎯 解決したい問題
「調べたい因子は3水準なのに、手元にあるのは2水準系の直交表(L8など)」
解決策:
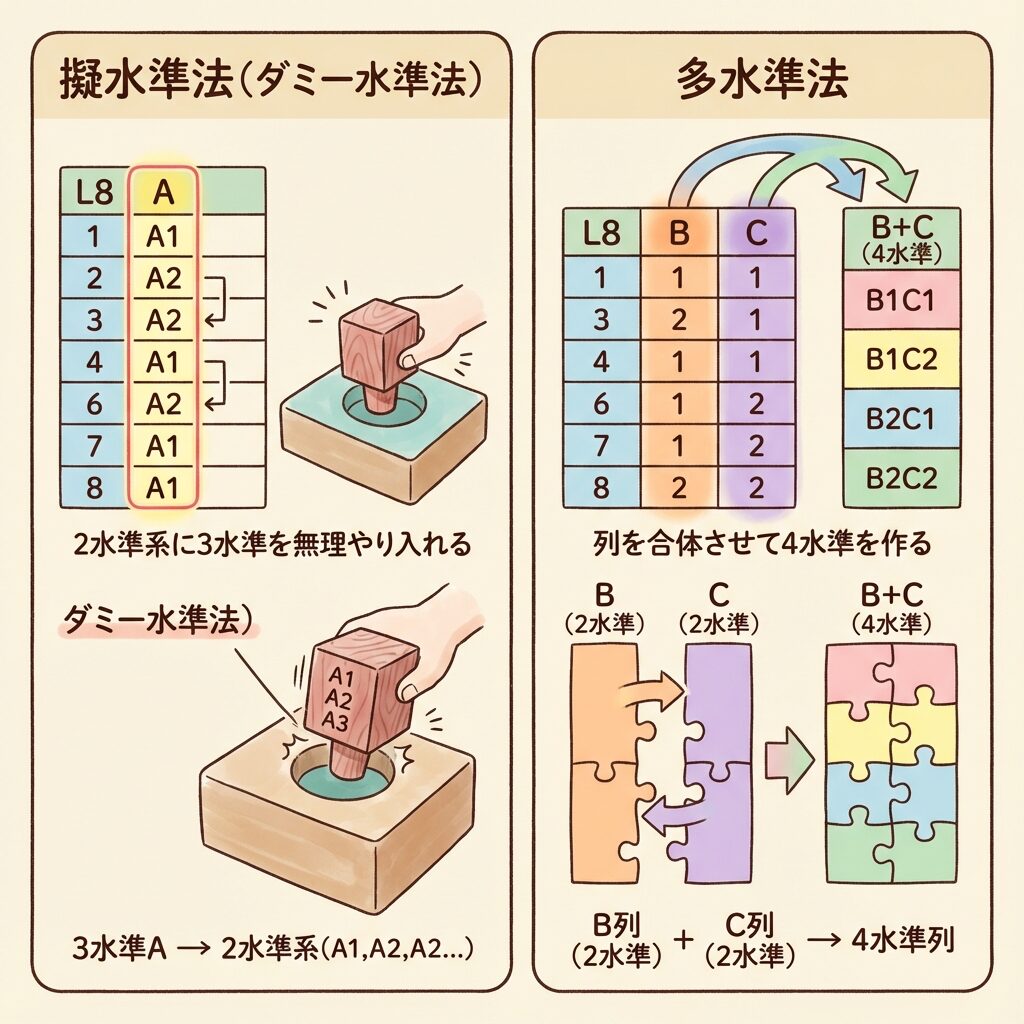
1つの水準を2回使って、擬似的に2水準として扱う
例:3水準(A1, A2, A3)→ 2水準として(A1, A2)と(A1, A3)…ではなく
(A1, A2, A2)のようにA2を2回出現させる
イメージ:「丸い穴に四角い棒を無理やり入れる」ような技法
🔺 多水準法(多水準作成法):水準を「増やしたい」ときに使う
🎯 解決したい問題
「調べたい因子は4水準なのに、手元にあるのは2水準系の直交表(L8など)」
解決策:
直交表の2つの列を組み合わせて、4水準を作る
例:列1(1, 2)×列2(1, 2)→(1-1, 1-2, 2-1, 2-2)の4通り
イメージ:「2つの列を合体させて、より大きな水準を作る」技法
📊 擬水準法 vs 多水準法:比較表
| 比較項目 | 擬水準法 | 多水準法 |
|---|---|---|
| 解決したい問題 | 3水準を2水準系に入れたい | 4水準を2水準系で作りたい |
| 水準数の変化 | 3 → 2(減らす) | 2 → 4(増やす) |
| やり方 | 1つの水準を繰り返し使う | 2つの列を組み合わせる |
| 使う列の数 | 1列のまま | 2列を消費 |
| イメージ | 無理やり押し込む | 合体させて大きくする |
「因子の水準数と直交表の水準数、どちらが大きい?」
・因子の水準 > 直交表の水準(3水準を2水準系に)→ 擬水準法
・因子の水準 > 直交表の水準(4水準を2水準系に)→ 多水準法
カテゴリ④:最適化(応答曲面法)
🎯 応答曲面法:最適な条件を「探索」する
🎯 解決したい問題
「どの因子が効くかはわかった。次は最適な条件(数値)を見つけたい」
具体例:
温度と圧力が収率に影響することはわかった。では、温度何℃、圧力何MPaが最適か?
特徴:
2次関数でデータをモデル化し、「山の頂上(最大値)」や「谷の底(最小値)」を探す
応答曲面法とは?最適条件を探すための実験設計 →
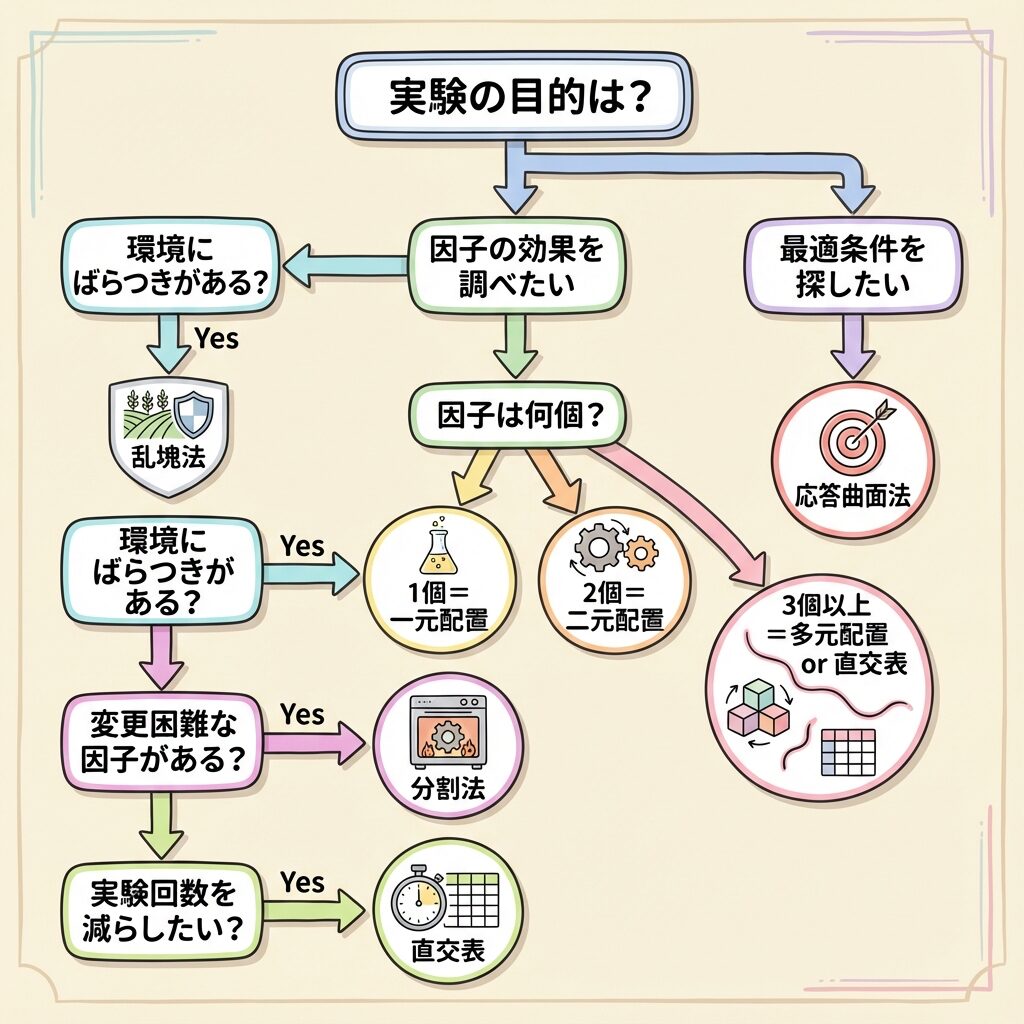
手法選択フローチャート:これで迷わない!
最後に、実験の状況に応じてどの手法を選べばよいかをフローチャートにまとめました。
Q1. 実験の目的は?
├─ 因子の効果を調べたい → Q2へ
└─ 最適条件を探したい → 応答曲面法
Q2. 調べたい因子は何個?
├─ 1個 → 一元配置実験
├─ 2個 → 二元配置実験
└─ 3個以上 → Q3へ
Q3. すべての組合せを試せる?
├─ YES → 多元配置実験(完全実施)
└─ NO(多すぎる) → 直交表を使う → Q4へ
Q4. 特殊な制約はある?
├─ 環境にバラつきがある → 乱塊法を組み合わせる
├─ 変更困難な因子がある → 分割法を使う
├─ 因子が入れ子になっている → 枝分かれ実験
├─ 3水準因子を2水準系直交表に入れたい → 擬水準法
└─ 4水準因子を2水準系直交表で作りたい → 多水準法
まとめ:迷ったときの判断基準
| こんなとき | 使う手法 |
|---|---|
| 因子が1〜2個 | 一元・二元配置 |
| 因子が多く実験回数を減らしたい | 直交表 |
| 環境のバラつきを除きたい | 乱塊法 |
| 因子の変更が難しい | 分割法 |
| 因子が入れ子構造 | 枝分かれ実験 |
| 3水準を2水準系に入れたい | 擬水準法 |
| 4水準を2水準系で作りたい | 多水準法 |
| 最適な数値条件を探したい | 応答曲面法 |
実験計画法の手法は多いですが、「なぜその手法が必要か」を理解すれば、選択に迷うことはありません。
この記事のフローチャートと比較表を保存しておけば、実務や試験で「どの手法を使えばいい?」と迷ったときに、すぐに答えが見つかるはずです。
📚 関連記事リンク集
■ 基本の配置実験
■ 特殊な状況への対応
■ 効率化の技法(直交表)
■ 最適化・その他
📚 実験計画法の「挫折」を救う2冊
「数式を見た瞬間に本を閉じた」
そんな経験がある私だからこそ推せる、厳選のバイブルです。