【完全保存版】サンプリング法の基礎知識｜単純無作為から2段抽出まで「なぜこの公式？」を完全図解

「サンプリング（標本抽出）」と聞くと、なんだか難しそうに感じますよね。

でも実は、私たちは日常生活で無意識にサンプリングをしています。味噌汁の味見がまさにそれです。鍋全体を飲み干さなくても、ひとさじ味見すれば「ちょっと薄いかな」とわかりますよね。

この記事では、統計学で登場する4つの主要なサンプリング法を、味噌汁やクラスの健康診断といった身近な例で徹底図解します。公式を「丸暗記」するのではなく、「なぜこの式になるのか」がスッキリわかる内容になっています。

サンプリング（標本抽出）とは？｜なぜ全部調べないのか

まず「サンプリングとは何か」を確認しておきましょう。

サンプリングの定義｜「一部を調べて全体を推測する」

サンプリング（標本抽出）とは、母集団（調べたい全体）から一部のデータ（標本）を取り出すことです。

なぜ全部調べないのでしょうか？理由は3つあります。

理由	具体例
① コストが高い	1億人の国民全員に調査するのは現実的ではない
② 時間がかかる	新製品の品質検査を全数行うと、発売が遅れる
③ 破壊検査	電球の寿命検査は、点灯し続けて壊れるまで調べる

特に③の破壊検査は重要です。全数検査をしたら、売る製品がなくなってしまいますよね。だからこそ、「一部を調べて全体を推測する」サンプリングが必要なのです。

サンプリングの目的｜「推測の精度」を上げたい

サンプリングの最終目的は、できるだけ少ないサンプルで、できるだけ正確に母集団を推測することです。

ここで重要なのが「推測の精度」です。統計学では、推測の精度を「標本平均の分散」で測ります。

これから紹介する4つのサンプリング法は、それぞれ分散を小さくする工夫が異なります。この視点を持って読み進めると、各手法の特徴がスッキリ理解できます。

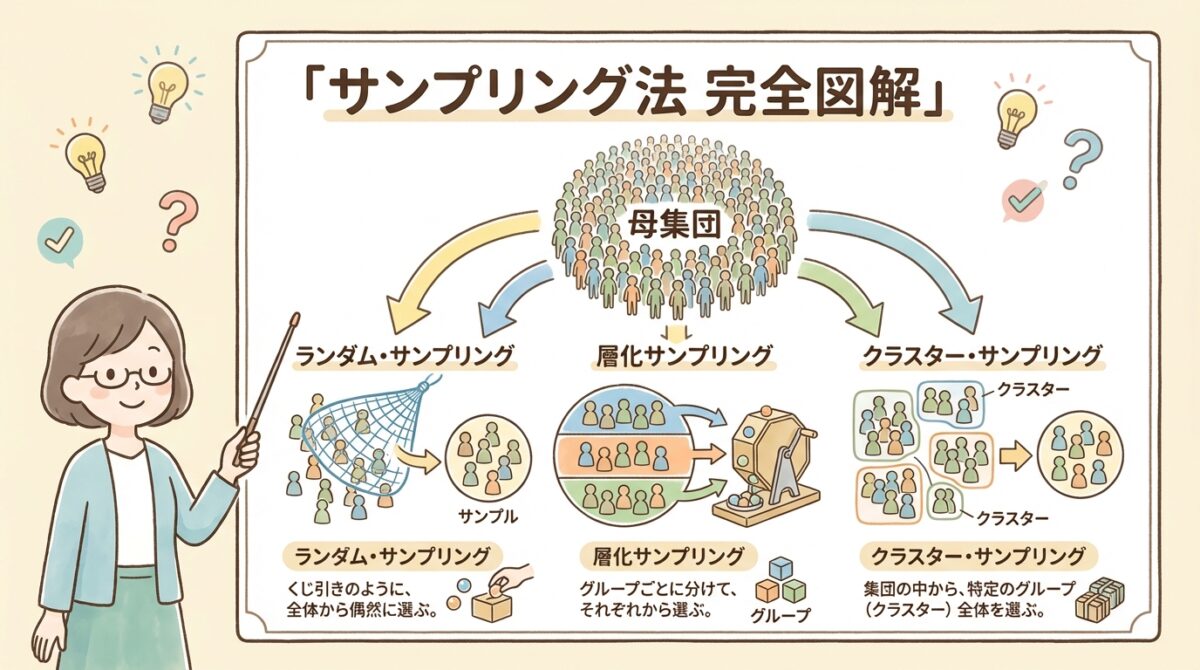
4つのサンプリング法の全体像｜特徴と使い分け

統計学で登場する主要なサンプリング法は、大きく分けて4種類あります。まずは全体像を把握しましょう。

サンプリング法	特徴	向いている場面
① 単純無作為抽出	くじ引きのように、完全にランダムに選ぶ	母集団が均質な場合
② 層別抽出	グループ分けしてから、各グループから抽出	母集団に明らかな層がある場合
③ クラスター抽出	グループをまるごと選び、その中を全数調査	コスト削減が重要な場合
④ 2段抽出	グループを選び、その中からさらに一部を抽出	大規模調査で精度とコストを両立

① 単純無作為抽出（SRS）｜すべてのサンプリングの基本

単純無作為抽出とは？｜「くじ引き」で選ぶ

単純無作為抽出（Simple Random Sampling: SRS）は、母集団から完全にランダムに標本を選ぶ方法です。

イメージは「くじ引き」です。箱の中に全員の名前が書かれた紙を入れて、目をつぶって引く。このとき、誰が選ばれるかは完全に運次第で、全員が同じ確率で選ばれます。

標本平均の分散公式｜なぜこの式になるのか？

単純無作為抽出で得た標本の平均 x̄ の分散は、以下の式で表されます。

【図解】なぜ σ²/n になるのか？

この式の意味を、図解で理解しましょう。

ステップ1：1個のデータのバラつき
母集団から1個のデータを取り出すとき、そのデータのバラつき（分散）は σ² です。これが「1回のくじ引きで、どれくらいハズレの可能性があるか」に相当します。

ステップ2：n個の平均を取ると…
n個のデータの平均を取ると、バラつきは「打ち消し合い」が起きます。あるデータが大きめでも、別のデータが小さめなら、平均すると真ん中に近づきます。

ステップ3：分散は n で割れる
独立なデータの平均の分散は、元の分散を n で割った値になります。これは「分散の加法性」と呼ばれる性質から導かれます。

非復元抽出と有限母集団修正（FPC）

実際の調査では、同じ人を2回選ぶことはありません（非復元抽出）。このとき、公式に有限母集団修正（FPC: Finite Population Correction）が加わります。

【図解】なぜ FPC が必要なのか？

FPCの意味を、トランプで例えましょう。

52枚のトランプから10枚引くとき、復元抽出（引いたら戻す）と非復元抽出（引いたら戻さない）では、後者のほうが「バラつきが小さく」なります。

なぜでしょうか？非復元抽出では、同じカードを2回引くことがないため、「極端に偏った標本」が出にくくなるのです。

抽出率 n/N	FPC の値	分散への影響
1%	約 0.99	ほぼ影響なし
10%	約 0.90	分散が10%減少
50%	約 0.50	分散が半分に
100%（全数）	0	分散ゼロ（当然！）

② 層別抽出（Stratified Sampling）｜「分けてから取る」で精度アップ

層別抽出とは？｜「似た者同士」をグループ化

層別抽出（Stratified Sampling）は、母集団を「層（Stratum）」と呼ばれるグループに分け、各層から一定数ずつサンプルを取る方法です。

イメージは「りんごの品質検査」です。

農園からりんごをサンプリングするとき、「Sサイズ」「Mサイズ」「Lサイズ」でまず分けてから、各サイズから同じ割合で取ります。こうすると、たまたまSサイズばかり選ばれる、という偏りを防げます。

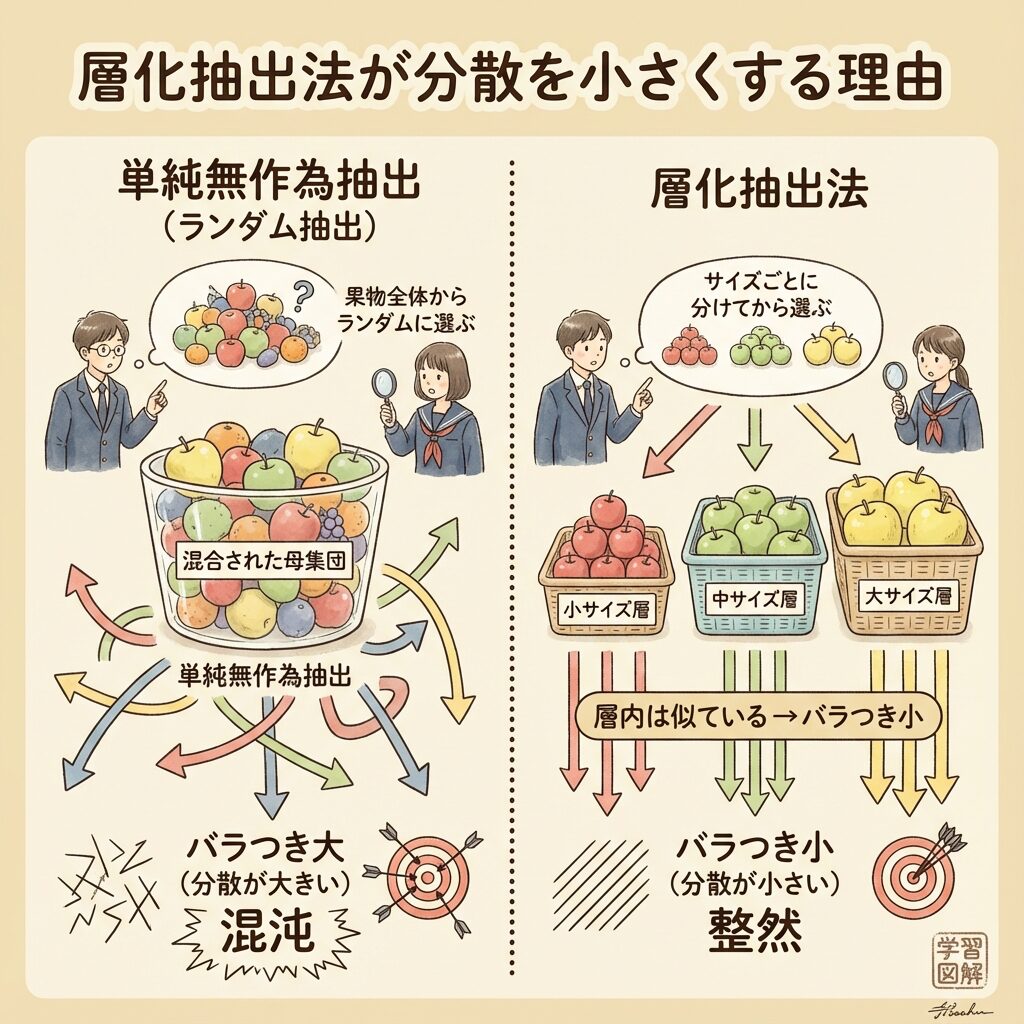
なぜ層別すると精度が上がるのか？｜分散の分解で理解

層別抽出が単純無作為抽出より精度が高くなる理由を、分散の分解で説明します。

【図解】分散は「層間」と「層内」に分解できる

母集団全体の分散 σ² は、以下のように分解できます。

層別抽出のポイントは、「層間分散を消せる」ことです。

単純無作為抽出では、たまたま特定の層に偏ることがあります。しかし層別抽出では、各層から確実にサンプルを取るため、層間のバラつきが標本に反映されません。

比例配分と最適配分｜各層から何個取るか

層別抽出では、「各層から何個ずつサンプルを取るか」を決める必要があります。主に2つの方法があります。

配分方法	考え方	使いどころ
比例配分	層の大きさに比例してサンプル数を決める	層内分散が同程度のとき
最適配分 （ネイマン配分）	バラつきが大きい層から多く取る	層ごとにバラつきが違うとき

③ クラスター抽出（Cluster Sampling）｜「グループごと」取る

クラスター抽出とは？｜コスト削減の切り札

クラスター抽出（Cluster Sampling）は、母集団を「クラスター（群）」に分け、いくつかのクラスターをまるごと選んで全数調査する方法です。

イメージは「学校の健康診断」です。

全国の中学生の平均身長を調べたいとき、全員を測るのは無理です。そこで、ランダムに選んだ学校の生徒を全員測るという方法が考えられます。これがクラスター抽出です。

クラスター抽出のメリット・デメリット

メリット	デメリット
調査コストが大幅に下がる	単純無作為より精度が落ちることが多い
移動コストを削減できる	クラスター間の差が大きいと偏りやすい
名簿がなくてもクラスター単位で調査可能	クラスターサイズが不揃いだと計算が複雑

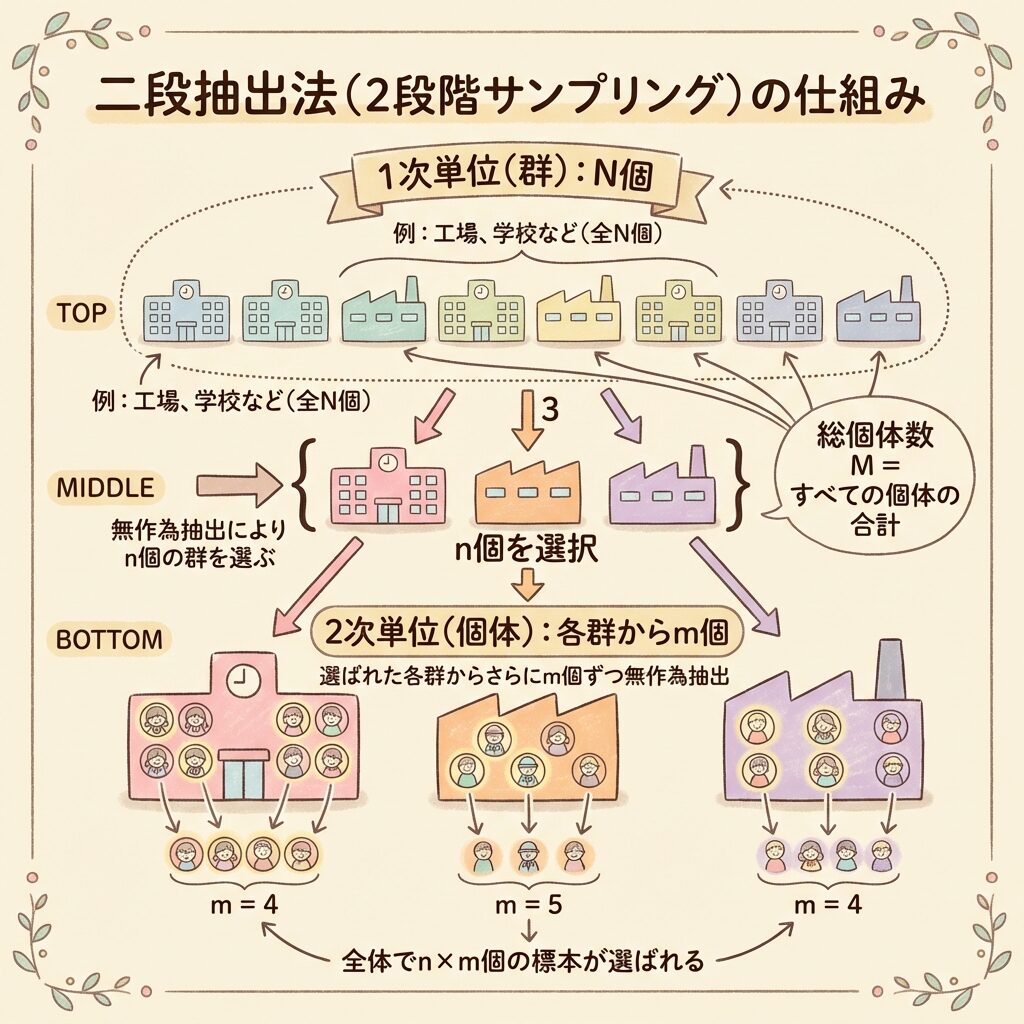
④ 2段抽出（Two-Stage Sampling）｜精度とコストの最適バランス

2段抽出とは？｜「群を選んで、その中からさらに選ぶ」

2段抽出（Two-Stage Sampling）は、クラスター抽出の発展形です。

クラスター抽出では、選んだ群を「全数調査」しましたが、2段抽出では選んだ群の中からさらに一部を抽出します。

【具体例】全国学力調査

全国の中学3年生の学力を調査するケースで考えてみましょう。

段階	抽出単位	具体例
1段目	群（1次単位）	全国1万校からランダムに100校を選ぶ
2段目	個体（2次単位）	各校から30人ずつランダムに選ぶ

こうすると、100校 × 30人 ＝ 3,000人の調査で、全国の傾向を把握できます。

2段抽出における標本平均の分散公式

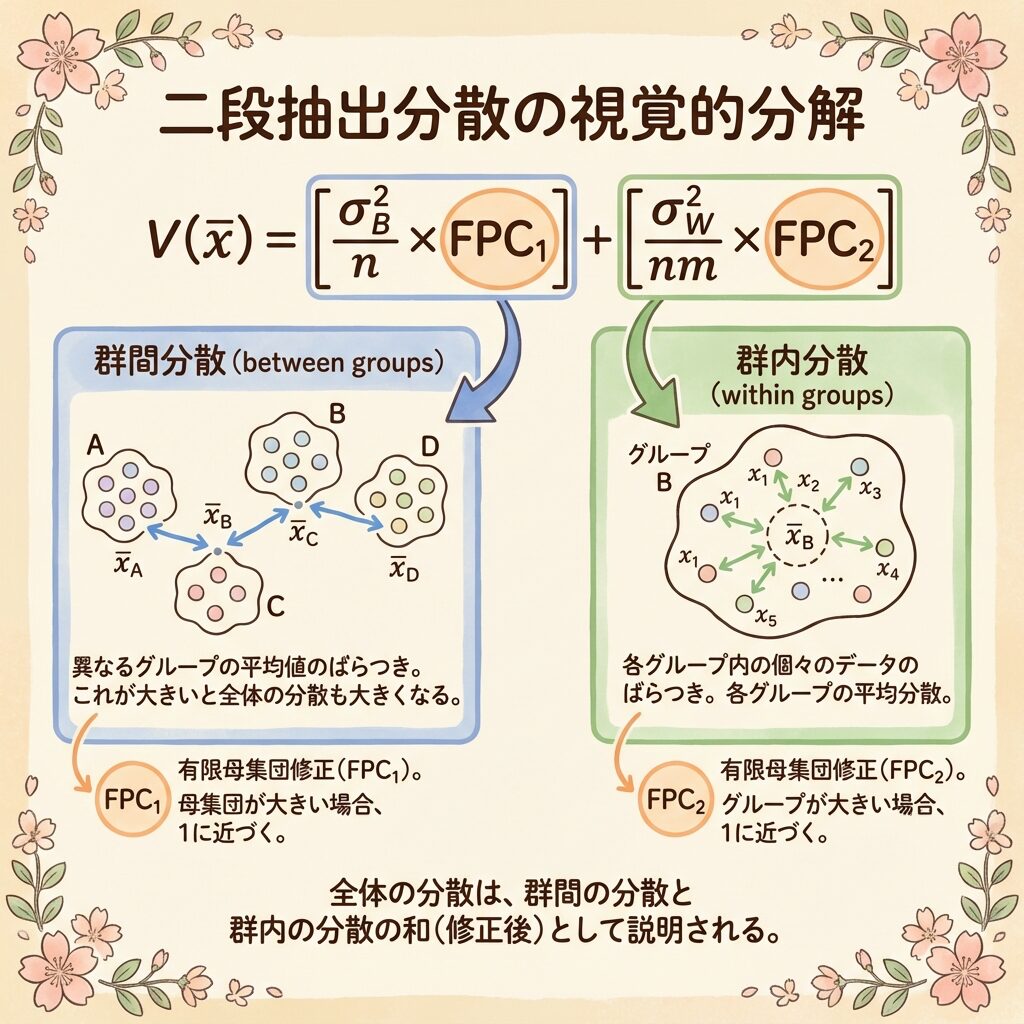
2段抽出の標本平均の分散は、以下の式で表されます。これが本記事の最重要公式です。

【図解】なぜこの式になるのか？

この公式は、「分散の加法性」から導かれます。2段抽出では、誤差が2つの段階で発生します。

【計算例】2段抽出の分散を求める

具体的な数値で計算してみましょう。

Step 1：第1項（群間由来の分散）を計算

Step 2：第2項（群内由来の分散）を計算

Step 3：合計して標本平均の分散を求める

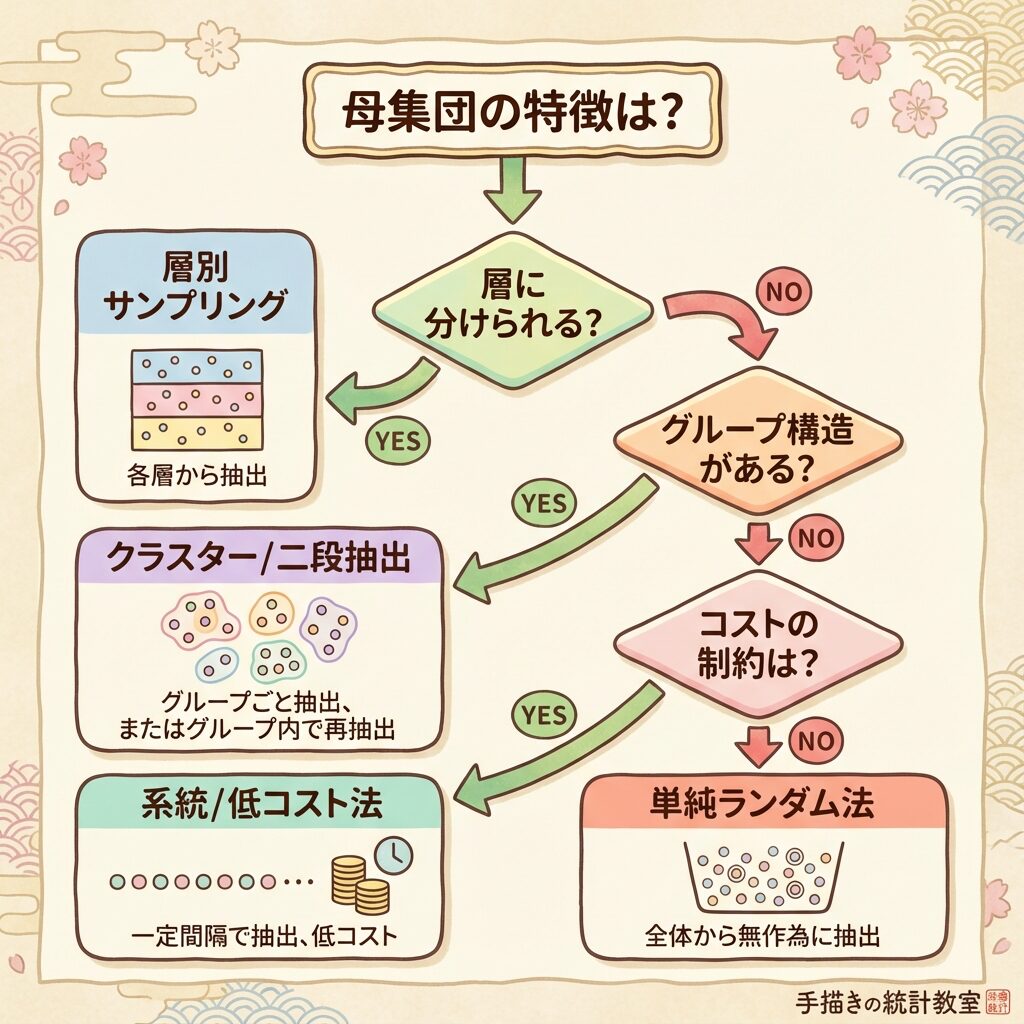
サンプリング法の選び方フローチャート

「どのサンプリング法を使えばいいの？」と迷ったときのために、選び方のフローチャートをまとめました。

条件	推奨サンプリング法
母集団が均質で、リスト（名簿）がある	単純無作為抽出
母集団に明確な「層」があり、層内は均質	層別抽出
コスト制約が厳しく、群単位でアクセス可能	クラスター抽出
大規模調査で、精度とコストを両立したい	2段抽出

まとめ｜サンプリング法の本質は「分散を減らす工夫」

この記事では、4つのサンプリング法の特徴と、公式の導出原理を解説しました。

サンプリング法を「丸暗記」するのではなく、「なぜそうなるのか」を理解すれば、応用問題にも対応できます。

ぜひ、計算例を自分で手を動かして解いてみてください。「頭でわかる」と「解ける」は別物です。