【完全図解】標本共分散と標本相関係数の求め方｜「n-1で割る理由」を中学生でもわかるように徹底解説

そもそも「共分散」とは何か？

共分散（きょうぶんさん）とは、「2つの変数が一緒に動く傾向」を数値化したものです。

例えば、「気温が上がるとアイスの売上が増える」という関係を考えてみてください。気温という変数と、アイスの売上という変数が同じ方向に動いているとき、共分散は正（プラス）になります。

逆に、「気温が上がるとおでんの売上が減る」という関係では、2つの変数が逆方向に動いているので、共分散は負（マイナス）になります。

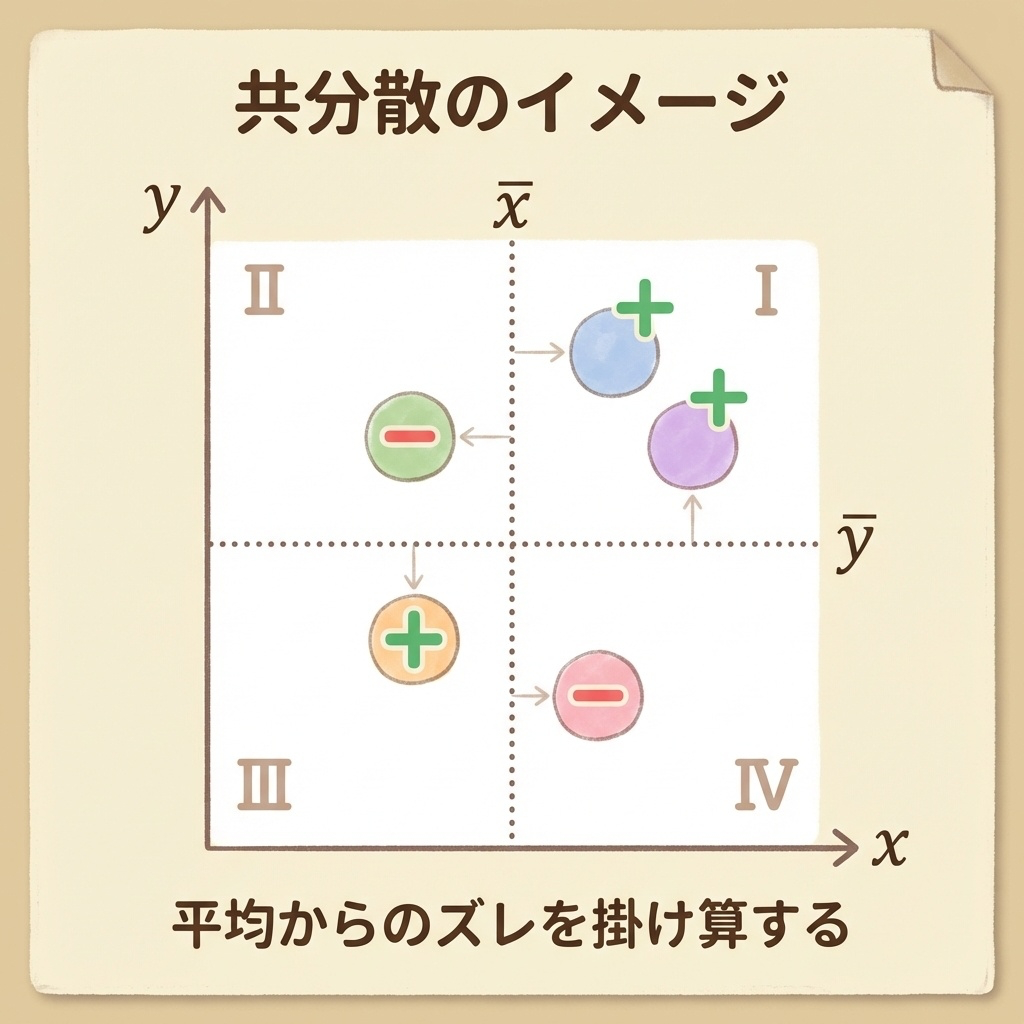
共分散の計算式を「イメージ」で理解する

共分散の計算は、散布図を「4つの象限」に分けて考えると理解しやすくなります。

横軸にxの平均（x̄）、縦軸にyの平均（ȳ）で線を引くと、散布図は4つの領域に分かれます。

象限	xの偏差	yの偏差	積の符号
第Ⅰ象限（右上）	＋（平均より大きい）	＋（平均より大きい）	＋
第Ⅱ象限（左上）	－（平均より小さい）	＋（平均より大きい）	－
第Ⅲ象限（左下）	－（平均より小さい）	－（平均より小さい）	＋
第Ⅳ象限（右下）	＋（平均より大きい）	－（平均より小さい）	－

つまり、右上と左下にデータが集まれば共分散はプラス（正の相関）、左上と右下にデータが集まれば共分散はマイナス（負の相関）になります。

この「偏差の積」をすべてのデータで合計し、平均したものが共分散です。

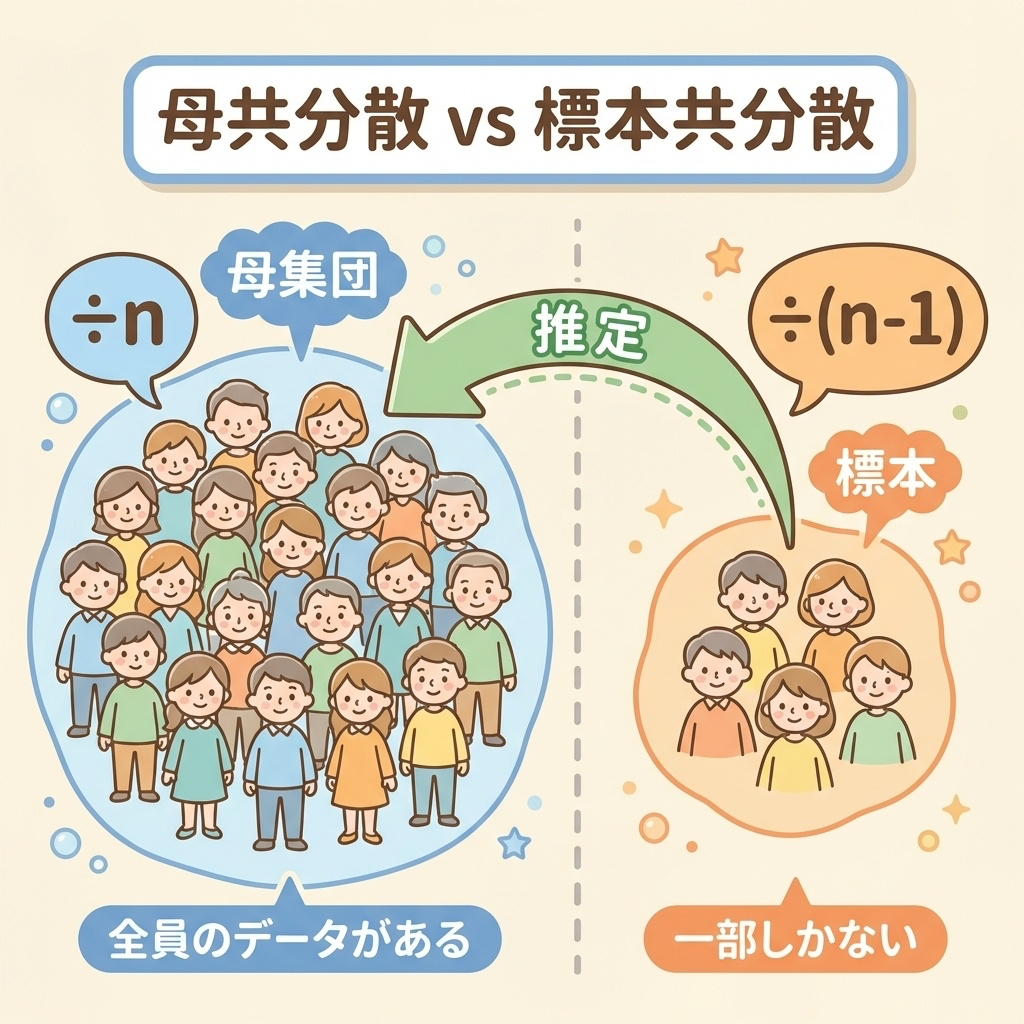
「母共分散」と「標本共分散」の違い

共分散には2種類あります。これを混同すると、計算結果が合わなくなるので注意が必要です。

母共分散（σxy）：母集団全体のデータがある場合

母集団（調べたい対象全体）のすべてのデータが手に入る場合に使う共分散です。

標本共分散（C_xy または S_xy）：サンプルデータしかない場合

実際の調査や実験では、母集団すべてを調べることは難しいですよね。だから「標本（サンプル）」を使って母集団の特徴を推定します。

この推定に使うのが標本共分散です。

区分	母共分散	標本共分散
記号	σxy	Cxy（または Sxy）
割る数	n	n - 1
使う平均	母平均 μ	標本平均 x̄, ȳ
用途	全数調査	サンプル調査

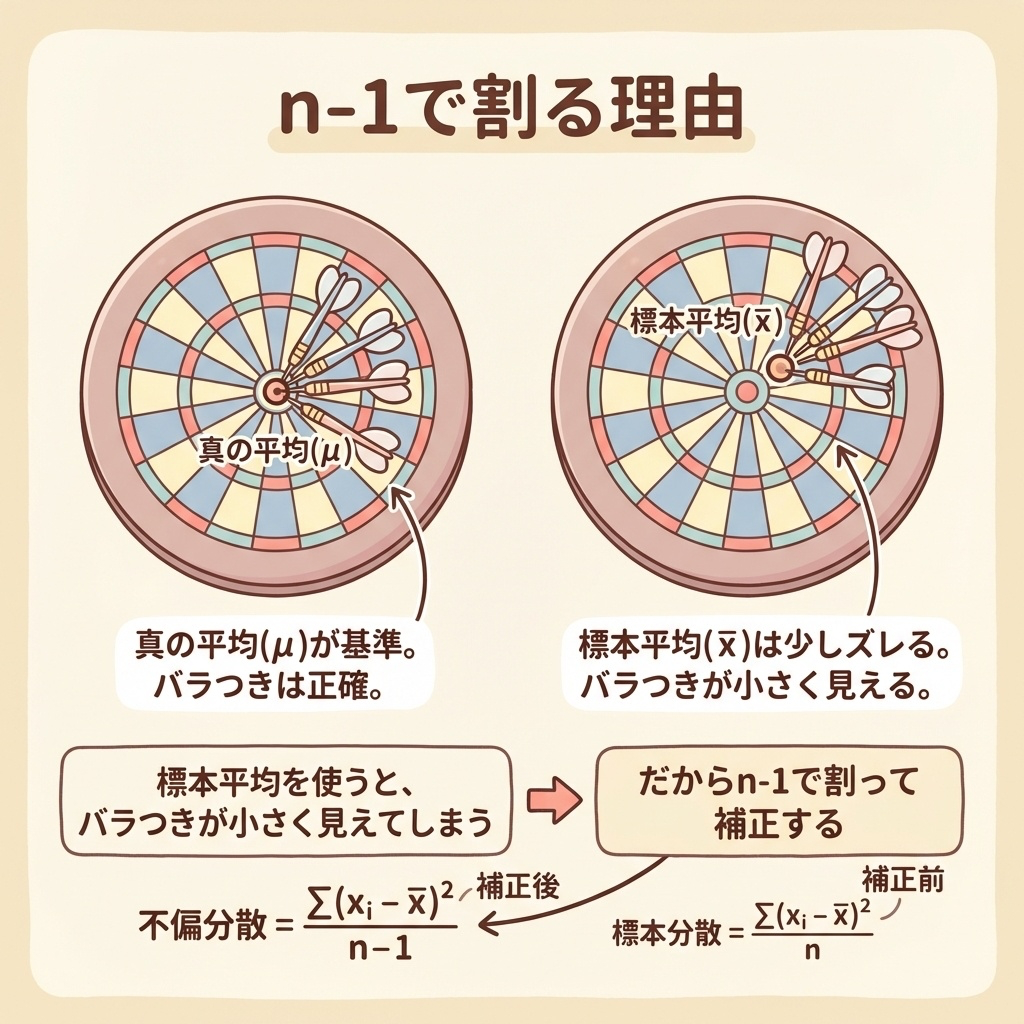
なぜ「n-1」で割るのか？直感的に理解する

「なぜ n ではなく n-1 で割るのか？」は、統計学を学ぶ人が必ずぶつかる疑問です。

これを理解するために、ダーツのたとえを使って説明します。

ダーツで考える「n-1で割る理由」

想像してください。あなたがダーツを投げたとします。

シナリオ①：的の中心（真の平均μ）がわかっている場合

もし「真の中心」がわかっていれば、各ダーツが中心からどれだけズレているか正確に測定できます。これが母共分散の考え方です。

シナリオ②：的の中心がわからず、ダーツの平均位置を使う場合

実際の調査では「真の中心」がわかりません。だから、投げたダーツの平均位置を「仮の中心」として使います。

ここで問題が起きます。ダーツの平均位置は、投げたダーツに近い場所に計算されます。つまり、各ダーツから平均位置までの距離は、真の中心からの距離より短く見えてしまうのです。

自由度という考え方

n-1 は「自由度」と呼ばれます。

5人のテストの点数があるとき、平均を計算すると1つの情報を使ってしまいます。すると、実際に「自由に動ける」データは 5-1 = 4個になります。

この「自由に動けるデータの数」が自由度であり、標本共分散や標本分散で n-1 で割る理由です。

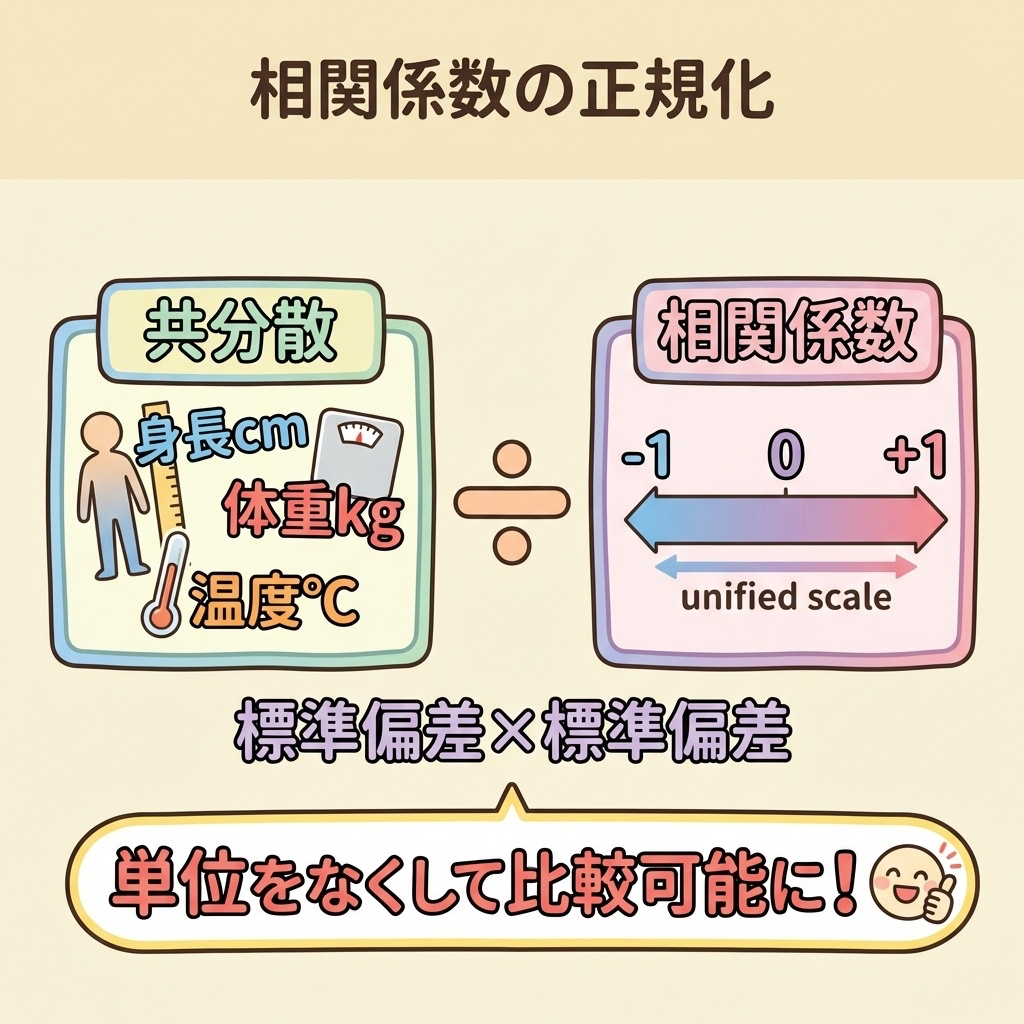
標本相関係数とは？「単位をなくす」魔法

共分散には1つ大きな問題があります。それは「単位がある」こと。

例えば、「身長(cm)と体重(kg)の共分散」と「気温(℃)とアイス売上(個)の共分散」を比べても、単位が違うので「どちらが強い関係か」がわかりません。

そこで登場するのが相関係数です。

相関係数 = 共分散を「標準偏差で割って」正規化したもの

相関係数は、共分散をxの標準偏差とyの標準偏差で割ることで、単位をなくし、-1から+1の範囲に収めます。

または、展開すると以下のようになります：

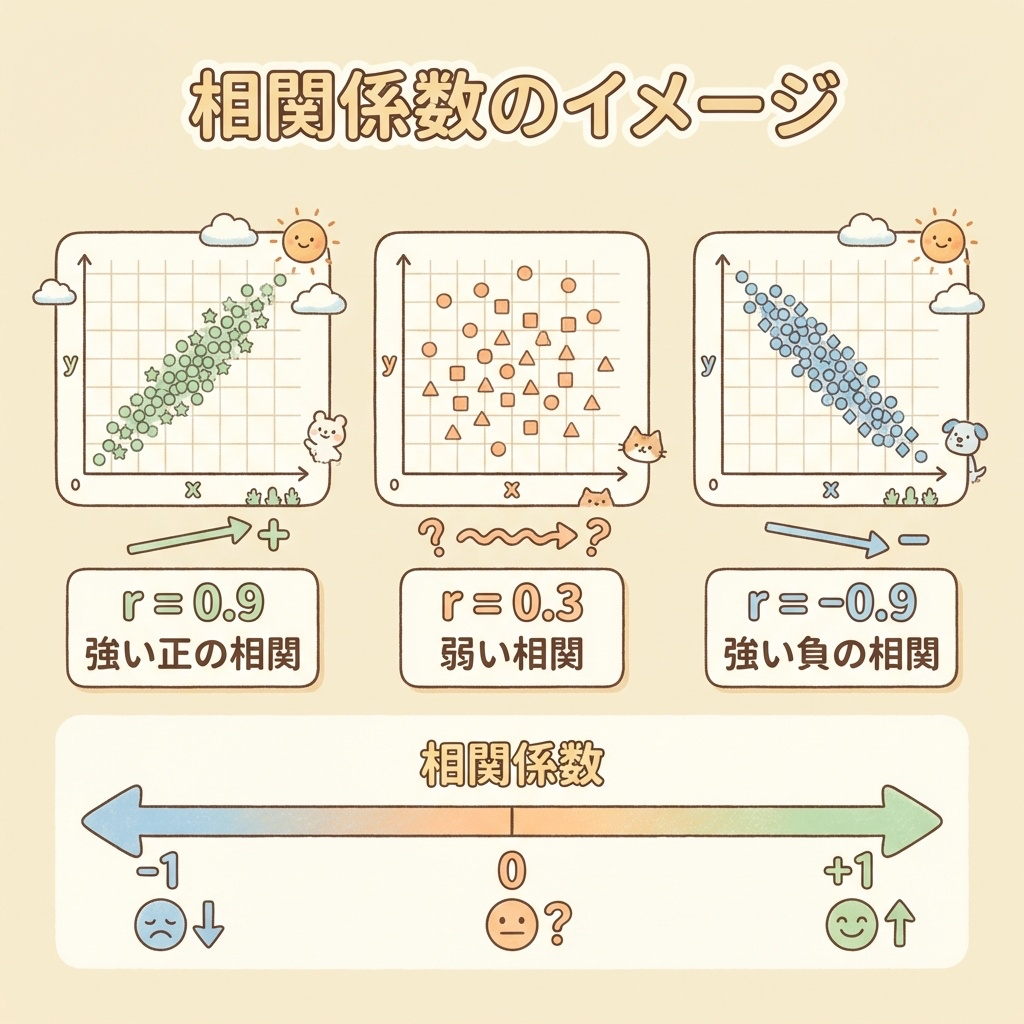
相関係数の解釈

相関係数 r	解釈	散布図のイメージ
0.7 ≤ r ≤ 1.0	強い正の相関	右上がりで点がまとまる
0.4 ≤ r < 0.7	中程度の正の相関	右上がりだがバラつく
0.2 ≤ r < 0.4	弱い正の相関	傾向はあるが散らばる
-0.2 < r < 0.2	ほぼ無相関	ランダムに散らばる
-1.0 ≤ r ≤ -0.7	強い負の相関	右下がりで点がまとまる

【実践】オリジナル例題で計算してみよう

それでは、実際に標本共分散と標本相関係数を計算してみましょう。以下のオリジナルデータを使います。

例題：勉強時間とテストの点数

ある塾で、5人の生徒の1週間の勉強時間 x（時間）とテストの点数 y（点）を調べました。

生徒	A	B	C	D	E
勉強時間 x（時間）	2	4	6	8	10
テスト点数 y（点）	45	55	70	75	85

求めるもの：標本共分散 C_xy と標本相関係数 r_xy

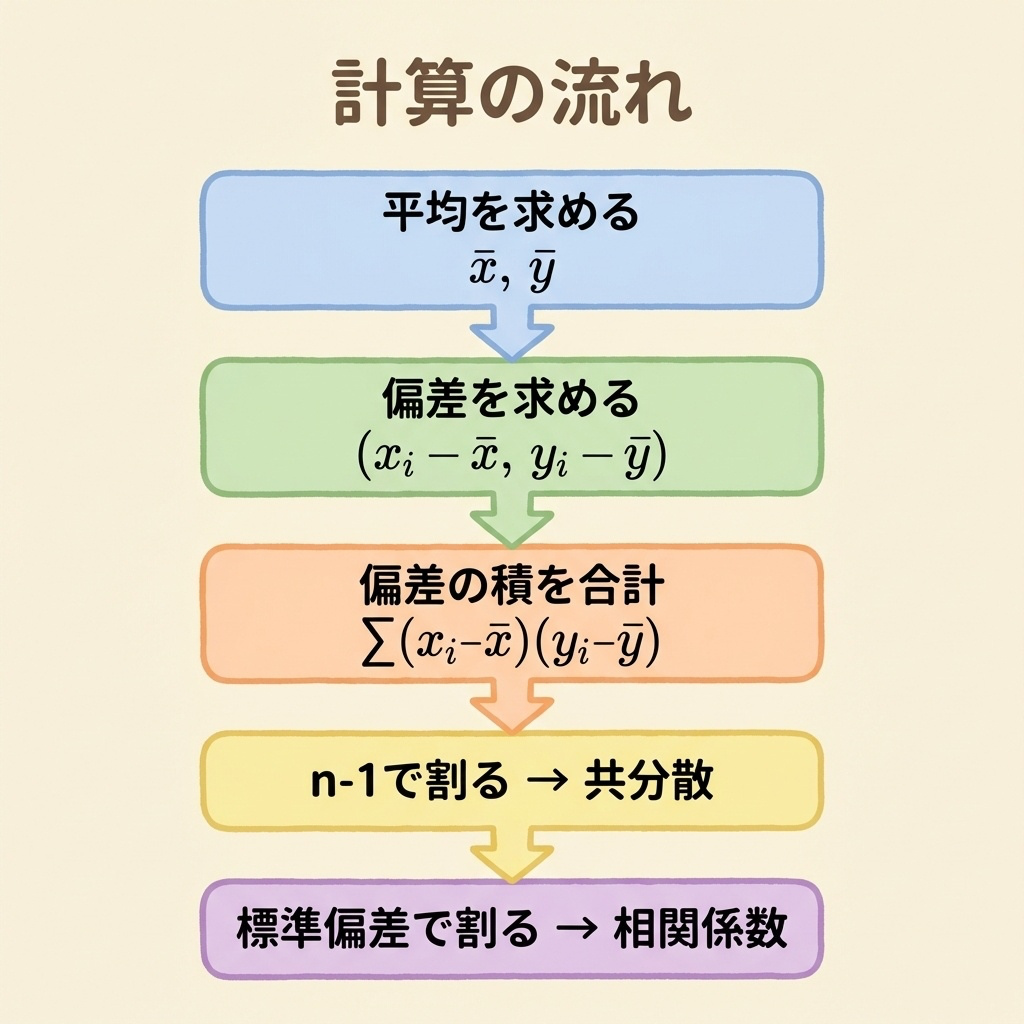
Step 1：平均を計算する

Step 2：偏差と偏差の積を計算する

生徒	xi	xi - x̄	yi	yi - ȳ	(xi-x̄)(yi-ȳ)
A	2	-4	45	-21	84
B	4	-2	55	-11	22
C	6	0	70	4	0
D	8	2	75	9	18
E	10	4	85	19	76
合計 Σ(xi-x̄)(yi-ȳ)					200

Step 3：標本共分散を計算する

共分散が正の値（50）なので、「勉強時間が増えるとテストの点数も上がる」という正の関係があることがわかります。

Step 4：標準偏差を計算する

相関係数を求めるには、xとyそれぞれの標本標準偏差が必要です。

生徒	(xi - x̄)²	(yi - ȳ)²
A	(-4)² = 16	(-21)² = 441
B	(-2)² = 4	(-11)² = 121
C	0² = 0	4² = 16
D	2² = 4	9² = 81
E	4² = 16	19² = 361
合計	40	1020

Step 5：標本相関係数を計算する

相関係数が0.99という非常に高い値なので、「勉強時間とテストの点数には強い正の相関がある」と言えます。

【別解】偏差積和から直接計算する方法

相関係数は、共分散を経由せず偏差の積と偏差の2乗から直接計算することもできます。この方法だと丸め誤差が少なくなります。

結果の解釈

指標	計算結果	解釈
標本共分散 Cxy	50	正の値 → 同じ方向に動く
標本相関係数 rxy	0.99	非常に強い正の相関

このデータからは「勉強時間を増やせば、テストの点数が上がる傾向がある」と言えます。ただし、相関関係は因果関係を保証するものではないことに注意してください。

まとめ：標本共分散と標本相関係数のポイント

項目	標本共分散 Cxy	標本相関係数 rxy
意味	2変数が一緒に動く傾向	共分散を正規化したもの
範囲	-∞ ～ +∞	-1 ～ +1
割る数	n - 1	（Cxyを使う）
単位	あり（x×yの単位）	なし（比較可能）