- L8直交表を使いたいのに、因子の水準が「3つ」で入らない…
- 「擬水準法」と「多水準作成法」の違いがわからない
- QC検定1級の過去問で擬水準法が出てきたけど、解説を読んでもピンとこない
- 「形式的な4水準因子P」って何?なぜ3列も使うの?
- 擬水準法とは何か、なぜ必要なのかが直感的にわかる
- 多水準作成法との違いを比較表でスッキリ整理
- L8直交表への3水準因子の割り付け方法を図解でマスター
- 「重要な水準を擬水準に選ぶ」理由がわかる
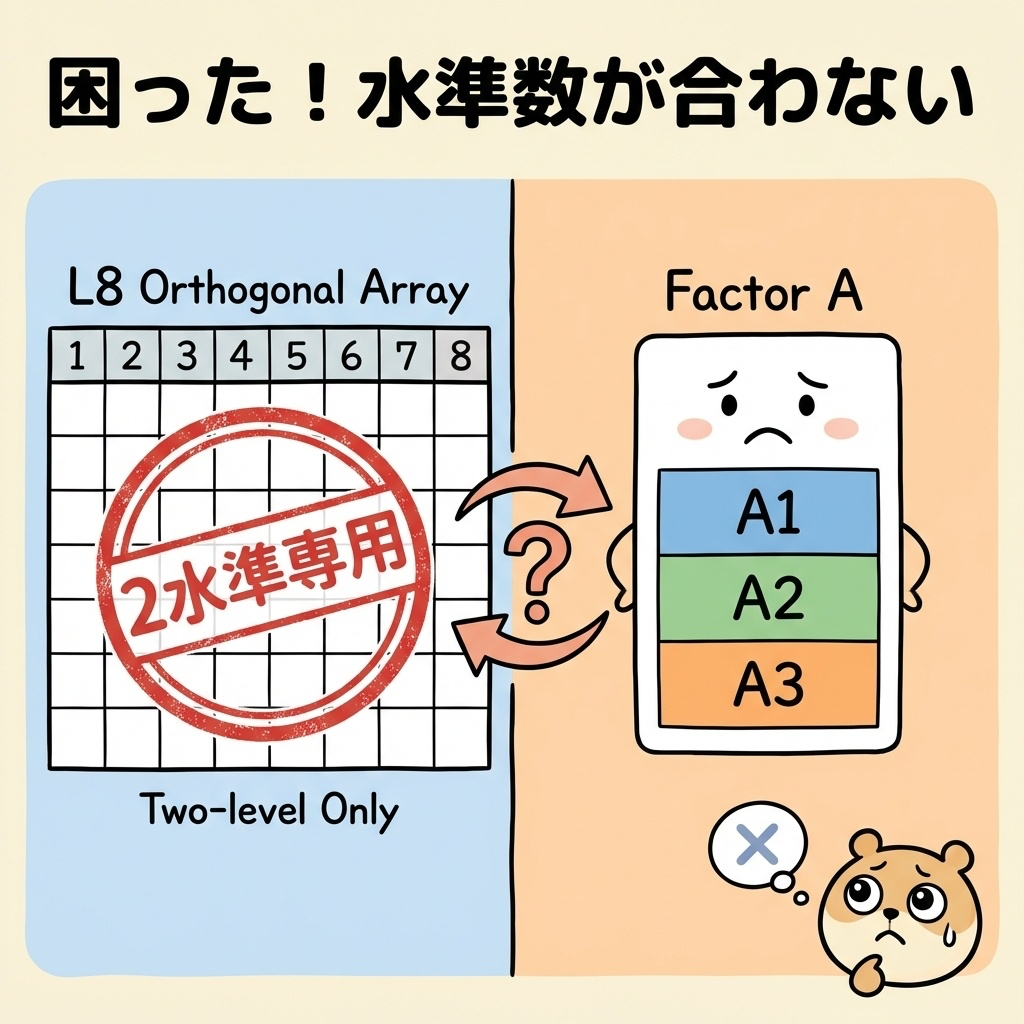
「L8直交表を使って実験を計画したいのに、因子Aの水準が3つある…」
こんな状況に直面したことはありませんか?
L8直交表は「2水準」の因子を割り付けるための表です。でも実務では、「温度を3段階で変えたい」「材料を3種類試したい」など、3水準の因子を扱いたい場面がよくありますよね。
そんなときに使える「裏技」が、今回解説する擬水準法(ぎすいじゅんほう)です。
この記事では、擬水準法の考え方を「なぜそうするのか?」から丁寧に解説します。QC検定1級でも頻出のテーマなので、しっかりマスターしていきましょう。
目次
そもそも何が問題なのか?|2水準系直交表と3水準因子のミスマッチ
まずは「なぜ擬水準法が必要なのか?」という問題の背景から理解しましょう。
L8直交表は「2水準専用」の表
L8直交表は、2水準の因子を最大7個まで割り付けられる便利な表です。
たとえば「温度(高/低)」「圧力(高/低)」「時間(長/短)」のように、各因子が2つの水準を持つ場合に使います。
- 実験回数:8回
- 列の数:7列
- 各列の水準:2水準(1と2)
- 割り付け可能な因子:最大7個(2水準因子)
でも実務では「3水準因子」を使いたい場面がある
ところが、実際の実験では「3つの水準を試したい」という場面がよくあります。
たとえば、こんなケースです。
- 材料の種類:材料X、材料Y、材料Z の3種類を比較したい
- 温度:100℃、150℃、200℃ の3段階で効果を見たい
- 添加量:少量、標準、多量 の3レベルで検証したい
このとき、「じゃあL9直交表(3水準系)を使えばいいのでは?」と思うかもしれません。
確かにそれも一つの選択肢です。でも、他の因子がすべて2水準だったらどうでしょう?
| 因子 | 水準数 | 具体例 |
|---|---|---|
| 因子A(材料) | 3水準 | X、Y、Z |
| 因子B(温度) | 2水準 | 低、高 |
| 因子C(圧力) | 2水準 | 低、高 |
このように「3水準因子が1つだけ」で、残りは2水準の場合、L9を使うと2水準因子の割り付けが難しくなります。
「できればL8を使いたい。でも3水準因子がある…」
この矛盾を解決するのが、擬水準法なのです。
2つの解決策|「多水準作成法」と「擬水準法」の違い
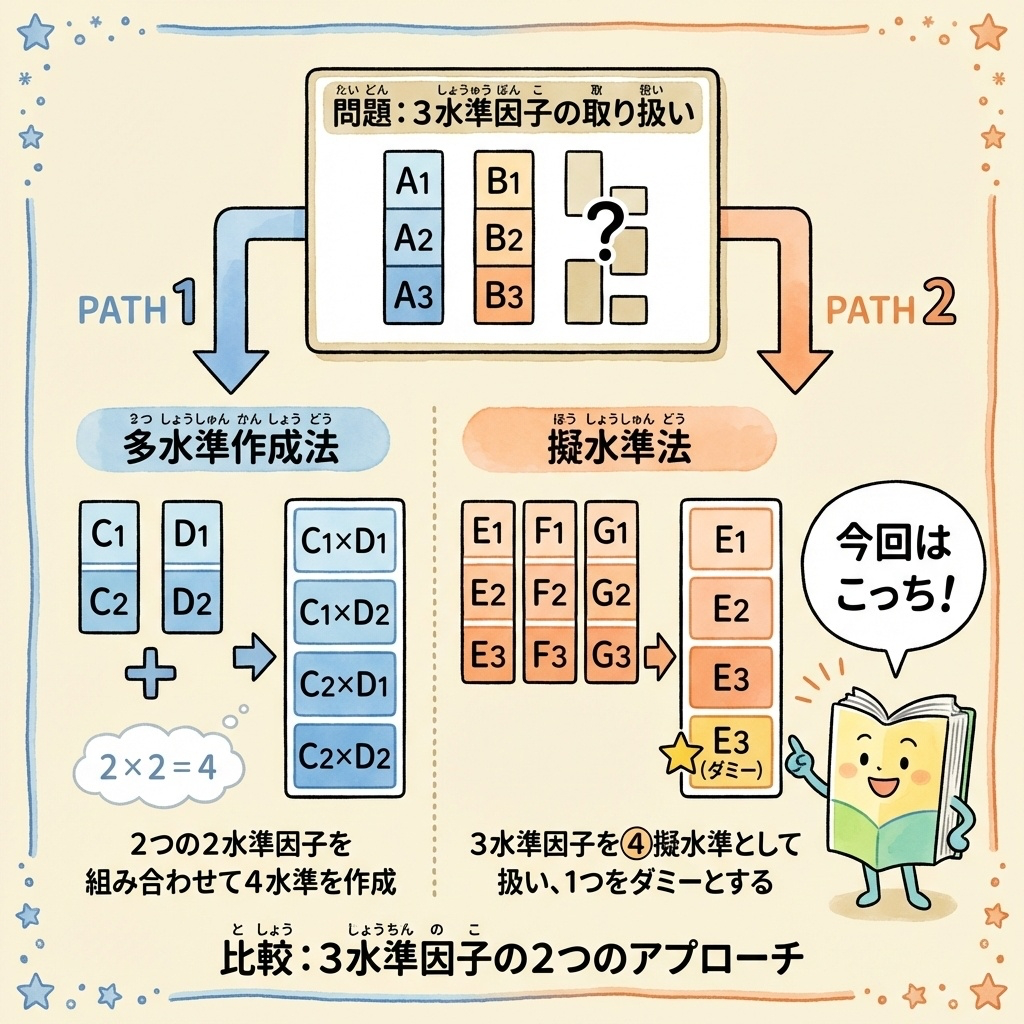
2水準系直交表に3水準以上の因子を入れる方法は、大きく分けて2つあります。
方法①:多水準作成法(4水準を作る)
多水準作成法は、2つの列を組み合わせて「4水準」を作る方法です。
たとえば、[1]列と[2]列を使うと、以下のように4つの組み合わせができます。
| [1]列 | [2]列 | 組み合わせ | 4水準因子 |
|---|---|---|---|
| 1 | 1 | (1,1) | 第1水準 |
| 1 | 2 | (1,2) | 第2水準 |
| 2 | 1 | (2,1) | 第3水準 |
| 2 | 2 | (2,2) | 第4水準 |
2列 × 2水準 = 4通りの組み合わせができるので、4水準の因子を割り付けられます。
でも、これだと「3水準」の因子には1つ水準が余ってしまいますよね。
方法②:擬水準法(3水準を入れる)
擬水準法は、多水準作成法を応用して「3水準因子」を割り付ける方法です。
考え方はシンプルです。
形式的に4水準を作り、そのうち1つの水準を「ダミー(擬水準)」として、
実際の3水準因子の「どれか1水準」を2回使う
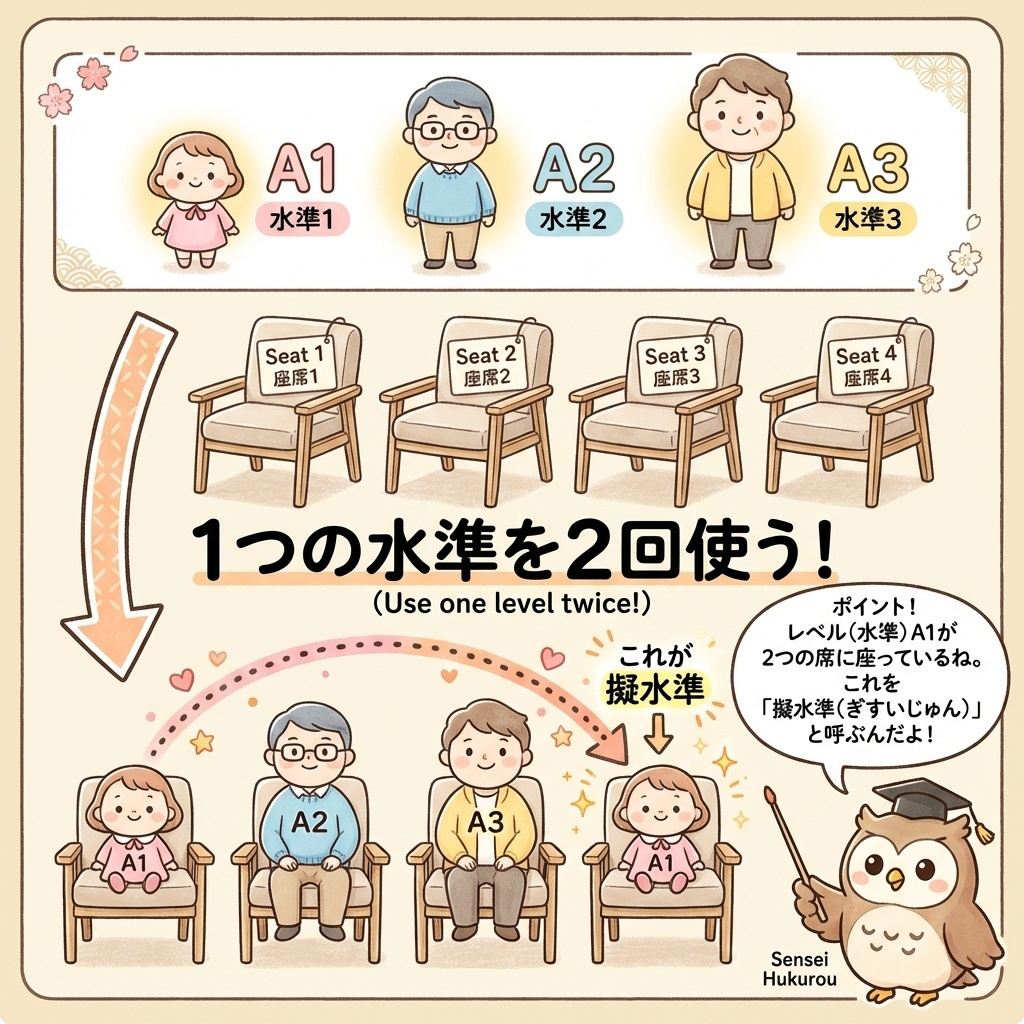
たとえば、4つの椅子(第1~第4水準)があって、座る人が3人(A₁、A₂、A₃)しかいない場合を想像してください。
1人が2つの椅子に座ることはできませんが、「同じ人が2回登場する」ことはできますよね。
- 第1水準 → A₁
- 第2水準 → A₂
- 第3水準 → A₃
- 第4水準 → A₁(もう一度登場) ← これが「擬水準」
この「A₁をもう一度使う」というのが擬水準法の核心です。
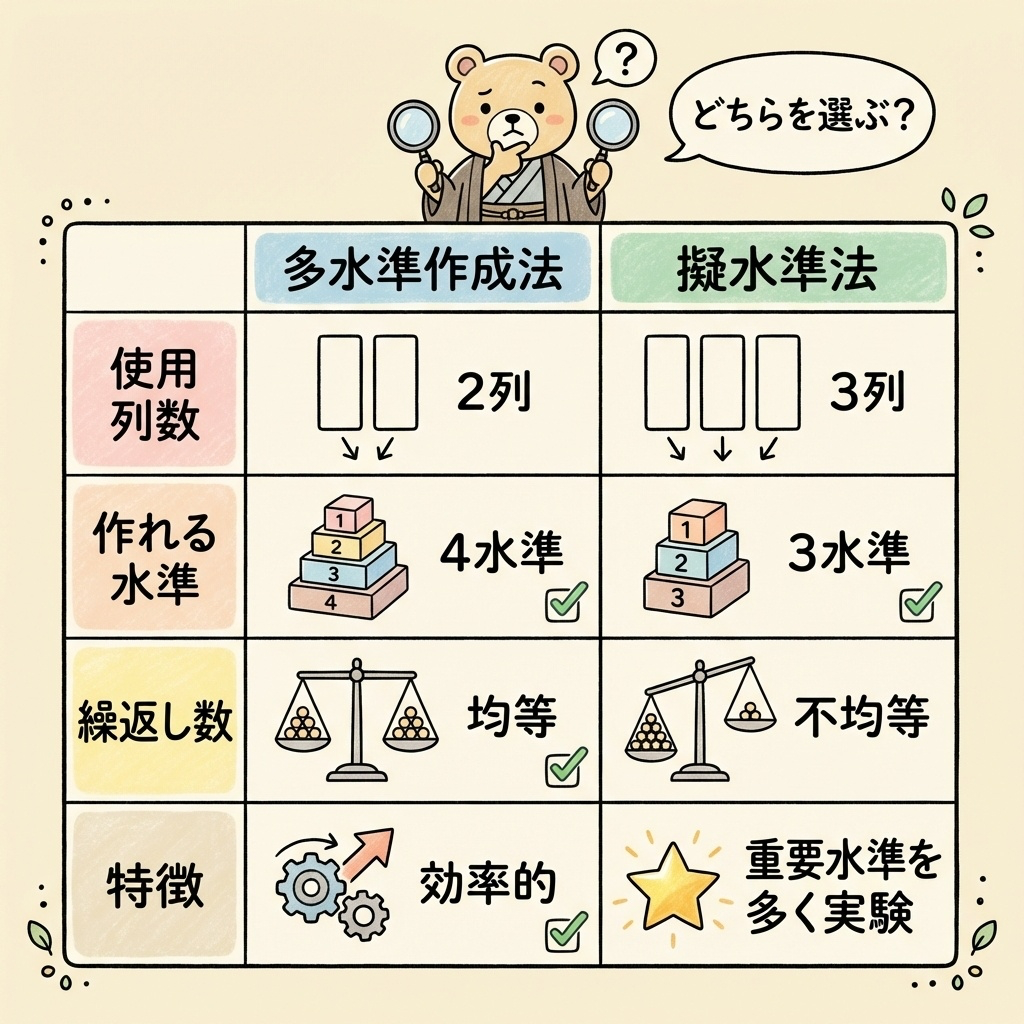
多水準作成法と擬水準法の比較
| 比較項目 | 多水準作成法 | 擬水準法 |
|---|---|---|
| 使用する列数 | 2列 | 3列(交互作用列を含む) |
| 作れる水準数 | 4水準 | 3水準(形式的には4水準) |
| 各水準の実験回数 | 均等(各2回ずつ) | 不均等(擬水準の水準は2倍) |
| 分散分析 | 列の平方和をそのまま使用 | 二元表を作成して再計算 |
| メリット | 計算がシンプル | 重要な水準を多く実験できる |
| 使う場面 | 4水準因子を入れたいとき | 3水準因子を入れたいとき |
擬水準法では、擬水準に選んだ水準(上の例ではA₁)の実験回数が他の水準の2倍になります。
そのため、「重要な水準」「詳しく調べたい水準」を擬水準に選ぶのがポイントです。
擬水準法の考え方|「1つの水準を2回使う」とは?
擬水準法の核心を、もう少し詳しく見ていきましょう。
イメージ:3人家族が4席のテーブルに座る
擬水準法を理解するために、こんな例え話を考えてみましょう。
レストランに行ったら、4人掛けのテーブルに案内されました。でも、あなたの家族は3人。1席余ってしまいます。
このとき、どうしますか?
- 選択肢A:空席のまま放置する → NG(実験では「空の水準」は作れない)
- 選択肢B:お父さんに2席分座ってもらう → OK(同じ人が2回登場)
擬水準法は、まさに「選択肢B」の発想です。
| 席(形式的4水準) | 座る人(実際の3水準) | 備考 |
|---|---|---|
| 席1(P₁) | お父さん(A₁) | - |
| 席2(P₂) | お母さん(A₂) | - |
| 席3(P₃) | 子ども(A₃) | - |
| 席4(P₄) | お父さん(A₁) | ← 擬水準(2回目の登場) |
この例では、「お父さん(A₁)」が席1と席4の両方に座っています。つまり、A₁の実験回数が他の水準の2倍になるわけです。
なぜ「重要な水準」を擬水準に選ぶのか?
擬水準に選んだ水準は、実験回数が2倍になります。
ということは、その水準に関するデータが多く集まるので、より精度の高い分析ができるということです。
だから、擬水準に選ぶのは:
- 重要な水準(本命の条件、最も知りたい条件)
- 実験しやすい水準(コストが低い、準備が簡単)
- 基準となる水準(現行条件、標準条件)
実務では、「現行の生産条件」を擬水準に選ぶことが多いです。現行条件のデータが多く集まれば、改善効果の比較がしやすくなりますからね。
擬水準法では、どの水準を擬水準に選ぶかが重要な設計判断になります。
「詳しく調べたい水準」「重要な水準」を選ぶのがコツです。
L8直交表への割り付け方法|3列を使って4水準を作る
では、具体的にL8直交表へ3水準因子を割り付ける方法を見ていきましょう。
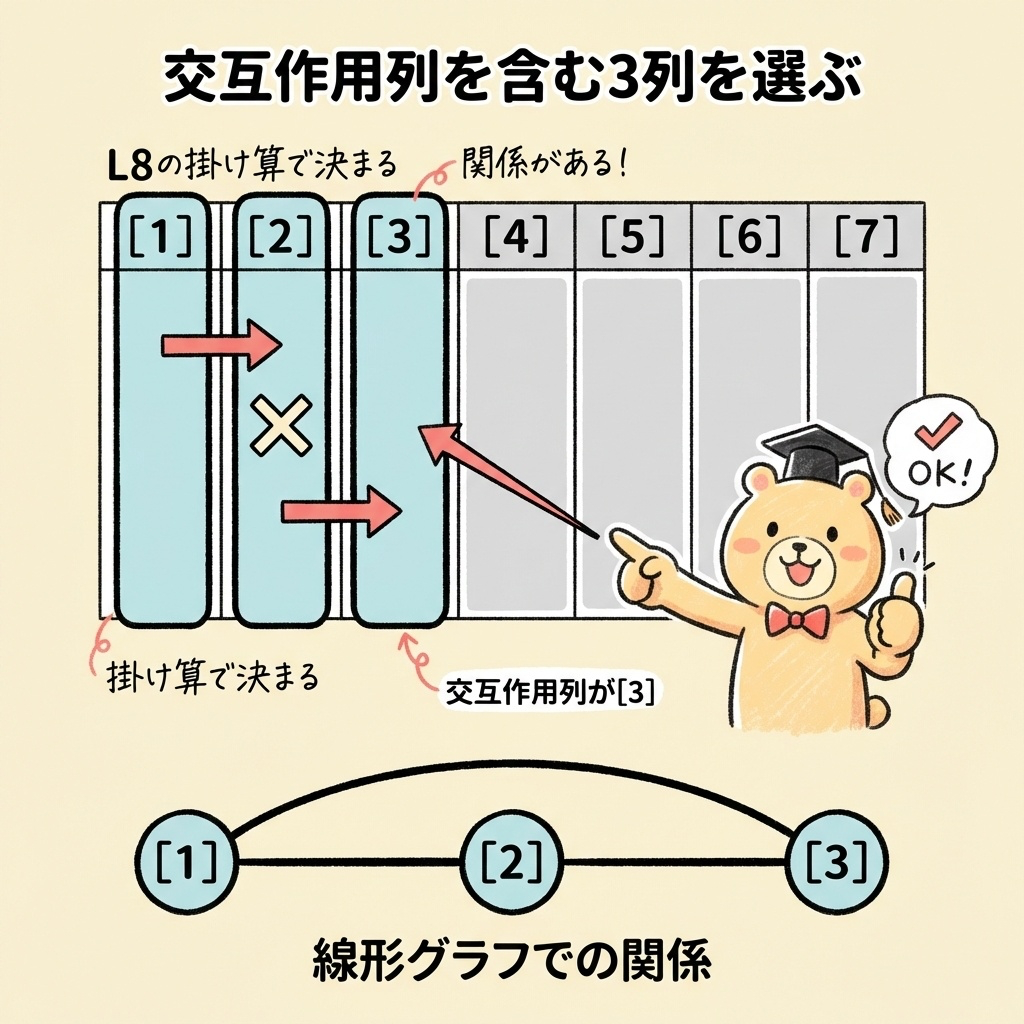
ステップ①:交互作用列を含む3列を選ぶ
擬水準法では、2つの列とその交互作用列(計3列)を使います。
L8直交表では、列同士の交互作用が別の列に現れる関係(交絡)があります。
たとえば、[1]列と[2]列の交互作用は[3]列に現れます。
- [1] × [2] = [3]
- [1] × [4] = [5]
- [2] × [4] = [6]
- [1] × [2] × [4] = [7]
擬水準法で3水準因子Aを割り付けるには、[1]列、[2]列、[3]列の3列を使います。
ステップ②:3列の組み合わせで形式的4水準因子Pを作る
[1]列、[2]列、[3]列の値の組み合わせを見ると、L8の8行で以下のパターンが現れます。
| 実験No. | [1]列 | [2]列 | [3]列 | 形式的4水準P |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | P₁ |
| 2 | 1 | 1 | 2 | P₁ |
| 3 | 1 | 2 | 2 | P₂ |
| 4 | 1 | 2 | 1 | P₂ |
| 5 | 2 | 1 | 2 | P₃ |
| 6 | 2 | 1 | 1 | P₃ |
| 7 | 2 | 2 | 1 | P₄ |
| 8 | 2 | 2 | 2 | P₄ |
ここで重要なのは、P₁~P₄がそれぞれ2回ずつ現れるということです。
つまり、形式的な4水準因子Pは、各水準が2回ずつ均等に実験されます。
上の表で「P₁、P₁、P₂、P₂…」と同じ水準が連続しているのは、直交表の並び順の関係です。
実際の実験はランダムな順序で行うので、連続実験による影響はありません。
ステップ③:形式的4水準Pと実際の3水準Aを対応させる
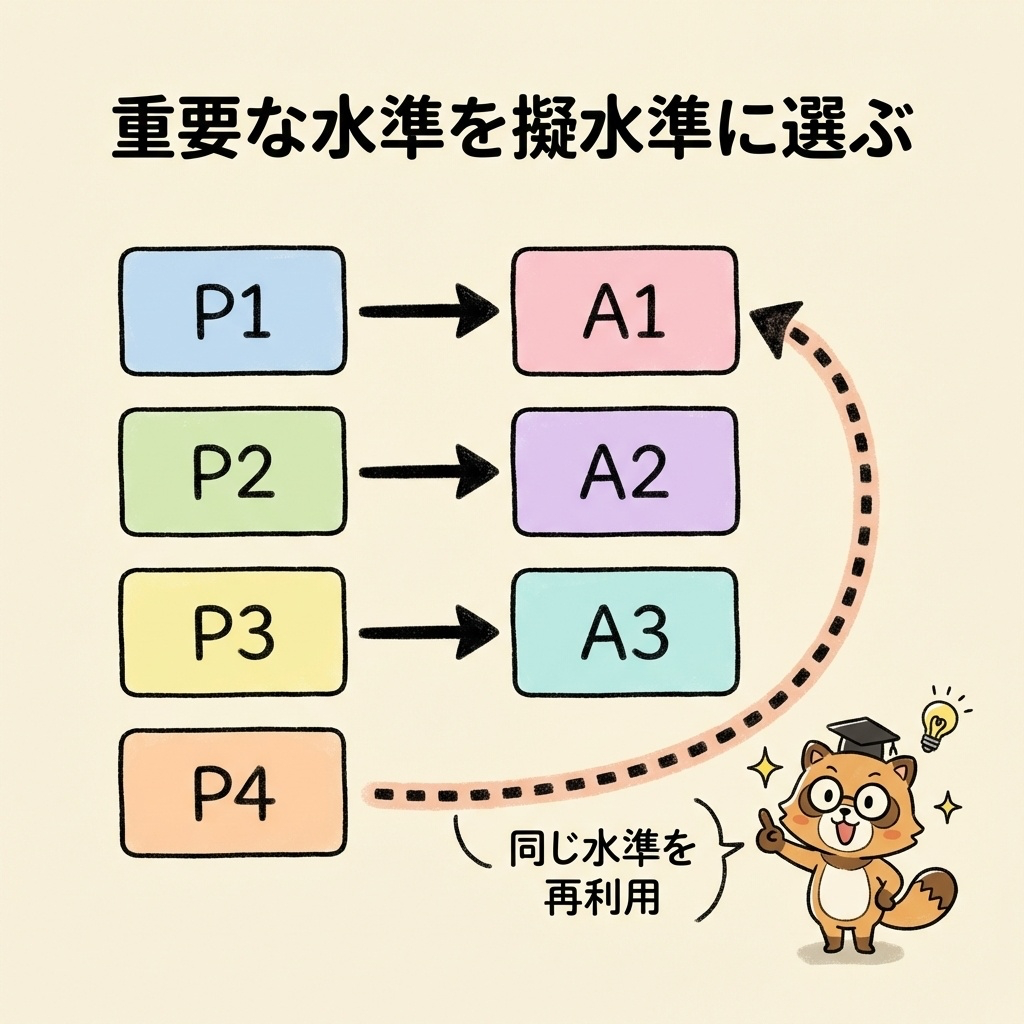
いよいよ、形式的な4水準(P₁~P₄)と実際の3水準(A₁、A₂、A₃)を対応させます。
ここで、どの水準を擬水準(2回使う水準)にするかを決める必要があります。
今回は、A₁を重要な水準として、擬水準に選ぶことにしましょう。
| 形式的4水準P | 実際の3水準A | 実験回数 |
|---|---|---|
| P₁ | A₁ | 2回 |
| P₂ | A₂ | 2回 |
| P₃ | A₃ | 2回 |
| P₄(擬水準) | A₁(再利用) | 2回 |
この対応関係により、最終的な各水準の実験回数は以下のようになります。
| 水準 | 対応するP | 合計実験回数 |
|---|---|---|
| A₁ | P₁ + P₄ | 4回(2倍) |
| A₂ | P₂ | 2回 |
| A₃ | P₃ | 2回 |
このように、A₁(擬水準に選んだ水準)は4回、A₂とA₃は各2回の実験になります。
擬水準法では、水準によって実験回数(繰返し数)が不均等になります。
この不均等さが、後の分散分析の計算に影響してきます(後編で詳しく解説)。
完成した割り付け表
以上をまとめると、L8直交表への割り付けは以下のようになります。
例として、因子A(3水準:材料X, Y, Z)と因子B(2水準:低, 高)を割り付ける場合を考えます。
| No. | [1] A |
[2] A |
[3] A |
[4] B |
[5] A×B |
[6] A×B |
[7] A×B |
因子A (実際) |
因子B (実際) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 材料X | 低 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 材料X | 高 |
| 3 | 1 | 2 | 2 | 1 | 2 | 1 | 2 | 材料Y | 低 |
| 4 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 材料Y | 高 |
| 5 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 材料Z | 低 |
| 6 | 2 | 1 | 1 | 2 | 2 | 1 | 2 | 材料Z | 高 |
| 7 | 2 | 2 | 1 | 1 | 2 | 2 | 1 | 材料X(擬) | 低 |
| 8 | 2 | 2 | 2 | 2 | 1 | 1 | 2 | 材料X(擬) | 高 |
黄色でハイライトした7行目と8行目が「擬水準」で、材料X(A₁)が再度登場しています。
まとめ|擬水準法の全体像
この記事では、擬水準法の考え方と割り付け方法を解説しました。
- 目的:2水準系直交表(L8など)に3水準因子を割り付ける
- 方法:3列を使って形式的4水準因子Pを作り、1水準を2回使う
- 擬水準の選び方:重要な水準、詳しく調べたい水準を選ぶ
- 結果:擬水準に選んだ水準の実験回数が2倍になる
- 注意点:分散分析では二元表を作成して計算する必要がある
擬水準法を使えば、L8直交表のまま3水準因子を扱えるので、実験計画の柔軟性が大きく広がります。
ただし、分散分析の計算は通常の直交表とは異なる方法が必要です。
次の【後編】では、擬水準を含む因子の平方和・自由度の計算方法を、具体的な例題で詳しく解説します。
- 擬水準を含む因子Aの平方和の求め方
- AB二元表の作成と繰返し数の違いへの対処
- 交互作用A×Bの平方和の計算
- 誤差の平方和の2つの求め方
- 自由度の計算方法
📚 次に読むべき記事
擬水準法の「兄弟分」である多水準作成法を理解すると、使い分けが明確になります。
実験計画法の全体像と学習順序を確認したい方はこちら。
【完全図解】L4直交表・L8直交表の使い方|割り付けの全手順 →
【実験計画法】線点図の正体|なぜ点と線?「L4」で学ぶ割り付け入門 →
【実験計画法】直交表(L8)の仕組み図解|なぜ「間引き」しても正しい結果が出るのか? →