- Welchの検定って、普通のt検定と何が違うの?
- 等価自由度φ*の計算式が複雑すぎて意味がわからない…
- 線形補間法って何?なぜこんな式になるの?
- QC検定の過去問で、t分布表から値を読み取る問題が解けない
- Welchの検定を使う場面と、計算の全手順
- 等価自由度φ*が「小数」になる理由
- 線形補間法の仕組みを「シーソー」でイメージ理解
- 例題を使った計算練習で、試験本番に対応できる力
「2つのグループの平均に差があるか?」を調べるt検定。統計学の基本中の基本ですよね。
でも、ここで大きな落とし穴があります。
普通のt検定(Studentのt検定)は、「2つのグループのバラつき(分散)が同じ」という前提で使うものなんです。もし分散が違う場合、普通のt検定を使うと、間違った結論を出してしまう危険があります。
そこで登場するのが「Welch(ウェルチ)の検定」。分散が違っていても正しく検定できる、より頑健(ロバスト)な手法です。
ただし、Welchの検定には1つ厄介な問題があります。それは自由度が小数になること。t分布表には整数の自由度しか載っていないので、「線形補間法」という技を使って、小数の自由度に対応するt値を求める必要があるんです。
この記事では、例題を使いながらWelchの検定の全手順を解説します。線形補間法の「なぜこの式になるのか?」も、シーソーのたとえでスッキリ理解できますよ。
目次
例題:2つの製造方法の品質を比較する
まずは例題を設定しましょう。実際に手を動かしながら学ぶのが一番です。
問題設定
ある部品の特性値Qは、製造工程の原料成分Rによって影響を受ける可能性がある。そこで、従来法(A法)と、工程変更によってR値を減少させる改善法(B法)を比較検討することにした。
両法で製造した部品をランダムにサンプリングして特性値Qを測定した結果、以下のデータを得た。特性値Qは小さいほど良い。
| サンプルサイズ n | データの合計 Σx | データの2乗の合計 Σx² | |
|---|---|---|---|
| 従来法(A法) | nA = 12 | ΣxA = 60.0 | ΣxA² = 310.00 |
| 改善法(B法) | nB = 8 | ΣxB = 36.0 | ΣxB² = 170.00 |
改善法(B法)は本当に特性値Qを下げる効果があるのか?を検定で確かめましょう。
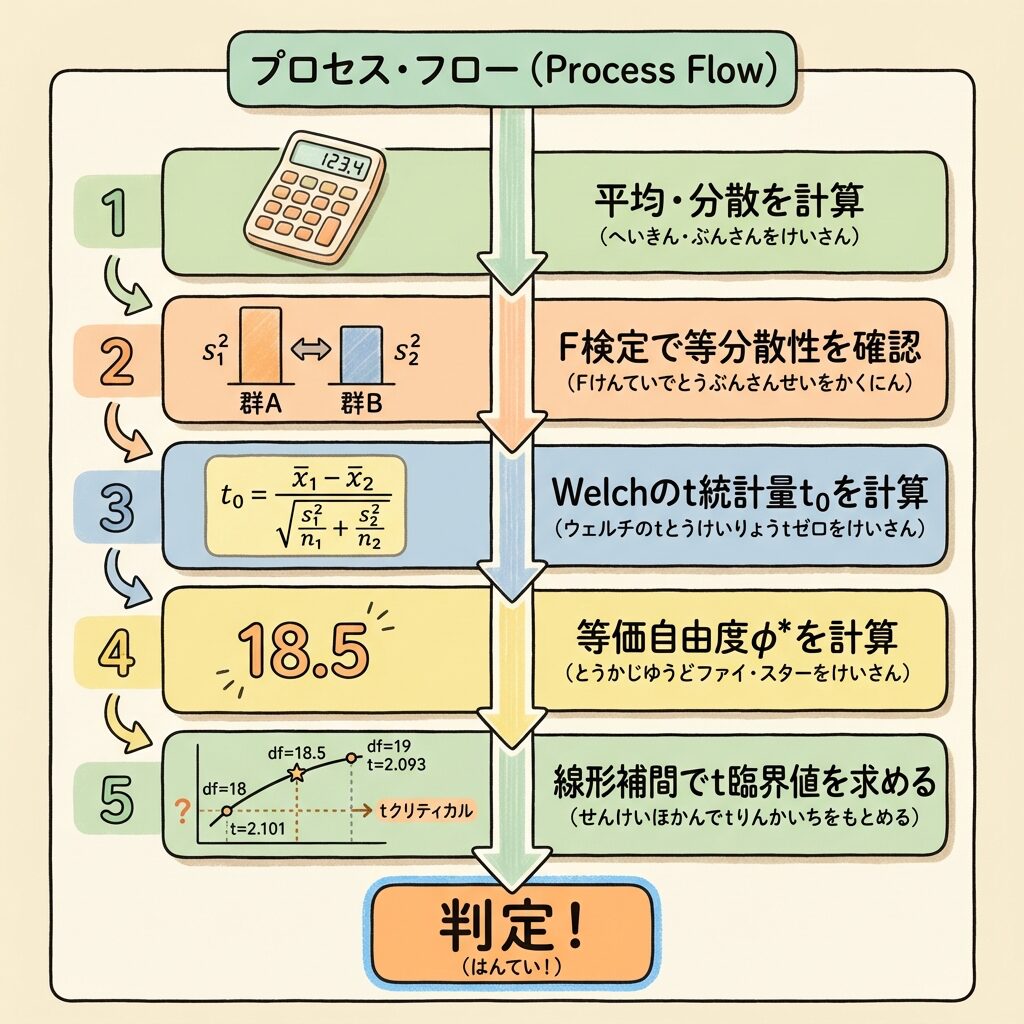
Step1:平均と分散を計算する
まずはデータの基本統計量を計算します。これがすべての土台になります。
平均値の計算
A法(従来法)の平均:
B法(改善法)の平均:
B法の方が平均値が小さいですね。でも、これが「偶然の差」なのか「本当の効果」なのかは、まだわかりません。
不偏分散の計算
A法の不偏分散:
VA = [310.00 − (60.0)²/12] ÷ (12−1)
= [310.00 − 300.00] ÷ 11
= 10.00 ÷ 11 = 0.909
B法の不偏分散:
VB = [170.00 − (36.0)²/8] ÷ (8−1)
= [170.00 − 162.00] ÷ 7
= 8.00 ÷ 7 = 1.143
計算結果のまとめ
| サンプルサイズ n | 平均値 x̄ | 不偏分散 V | 自由度 φ | |
|---|---|---|---|---|
| A法 | 12 | 5.00 | 0.909 | 11 |
| B法 | 8 | 4.50 | 1.143 | 7 |
Step2:等分散性を確認する(F検定)
次に、「2つのグループの分散は同じとみなせるか?」を確認します。これによって、普通のt検定を使うか、Welchの検定を使うかが決まります。
F値の計算
※常に大きい方を分子にする(F₀ ≥ 1)
等分散性の判定
F₀ < 2.0 → 等分散とみなせる
F₀ ≥ 2.0 → 等分散でない可能性あり
今回の F₀ = 1.257 は 2.0 未満なので、等分散とみなせます。
「あれ?等分散ならWelchの検定は不要では?」と思いましたか?
実は、Welchの検定は等分散でも使えます。等分散の場合、Welchの検定は普通のt検定とほぼ同じ結果になります。逆に、等分散でない場合は、Welchの検定の方が正確な結果を出せます。
つまり、「迷ったらWelch」という戦略が有効なんです。今回は練習のため、Welchの検定で進めましょう。
Step3:仮説を設定する
検定を行う前に、「何を証明したいのか」を明確にしましょう。
仮説の設定
| 帰無仮説 H₀ | μA = μB(A法とB法の母平均に差はない) |
| 対立仮説 H₁ | μA > μB(A法の方がB法より母平均が大きい) |
| 有意水準 | α = 0.05(5%) |
「特性値Qは小さいほど良い」ので、B法(改善法)が優れているなら、μA > μBとなるはずです。これを片側検定で確かめます。
Step4:Welchの検定統計量 t₀ を計算する
いよいよWelchの検定の核心部分です。
Welchの検定統計量の公式
この式の意味を分解すると:
- 分子:2つの平均の差(これが大きいほど「差がある」証拠)
- 分母:「平均の差のバラつき」を表す標準誤差(これが小さいほど信頼できる)
分母の計算(標準誤差)
VA/nA + VB/nB = 0.909/12 + 1.143/8
= 0.0758 + 0.1429
= 0.2187
√0.2187 = 0.4677
t₀ の計算
t₀ = (5.00 − 4.50) ÷ 0.4677
= 0.50 ÷ 0.4677
t₀ = 1.069
Step5:等価自由度 φ* を計算する
ここがWelchの検定の最大の特徴です。自由度が小数になるんです。
なぜ等価自由度が必要なのか?
普通のt検定では、自由度は φ = nA + nB − 2 で簡単に計算できます。
しかしWelchの検定では、2つのグループの分散が異なることを考慮する必要があります。分散が大きいグループほど「情報が不安定」なので、そのぶん自由度を調整するんです。
その結果、自由度が小数になります。これを「等価自由度」と呼びます。
Welch-Satterthwaiteの公式
φA = nA − 1、φB = nB − 1
複雑に見えますが、順番に計算すれば大丈夫です。
分子の計算
(VA/nA + VB/nB)² = (0.2187)² = 0.04783
分母の計算
(VA/nA)²/φA = (0.0758)²/11 = 0.000522
(VB/nB)²/φB = (0.1429)²/7 = 0.002916
合計 = 0.003438
φ* の計算
φ* = 0.04783 ÷ 0.003438
φ* = 13.91
普通のt検定なら自由度は 12 + 8 − 2 = 18 ですが、Welchの検定では 13.91 と小さくなりました。これは、分散の違いを考慮した結果です。
Step6:線形補間法でt臨界値を求める
ここが多くの人がつまずくポイントです。じっくり解説しますね。
なぜ線形補間が必要なのか?
t分布表には整数の自由度しか載っていません。
例えば φ = 13 や φ = 14 のt値は表から読めますが、φ* = 13.91 のt値は表にありません。
そこで、φ = 13 と φ = 14 のt値から、φ* = 13.91 のt値を推定するのが線形補間法です。
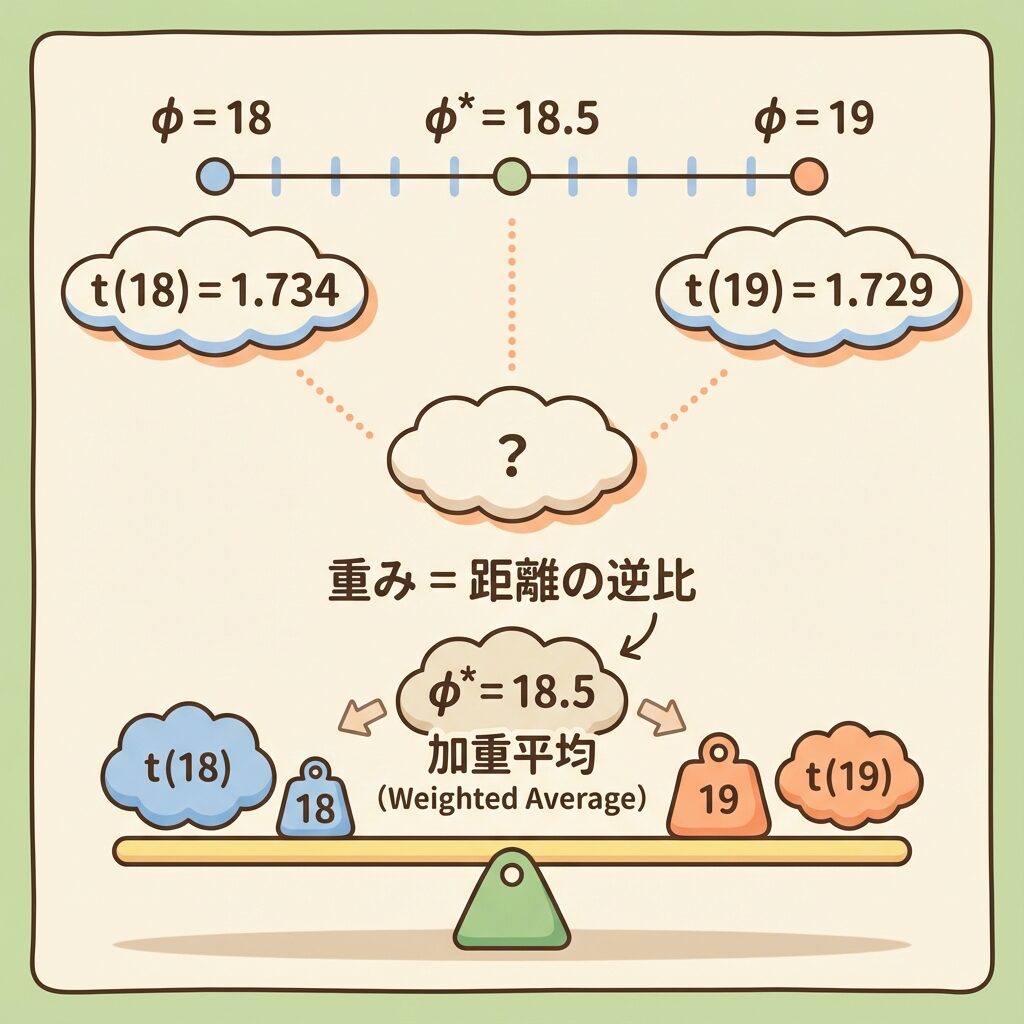
線形補間の仕組み:シーソーで考える
線形補間は「シーソーのバランス」でイメージするとわかりやすいです。
シーソーの両端に「φ = 13のt値」と「φ = 14のt値」が乗っています。
φ* = 13.91 は14に近いので、シーソーの支点を14側に寄せます。
すると、14側のt値の影響が大きくなります。
これを数式で表したのが、線形補間の公式です。
線形補間の公式
t(φ*, 2α) = w₁ × t(φ₁, 2α) + w₂ × t(φ₂, 2α)
ここで:
- φ₁ = φ*より小さい整数(今回は13)
- φ₂ = φ*より大きい整数(今回は14)
- w₁ = (φ₂ − φ*) / (φ₂ − φ₁) ← φ₁側の重み
- w₂ = (φ* − φ₁) / (φ₂ − φ₁) ← φ₂側の重み
φ*に近い方のt値ほど、重みが大きくなるという仕組みです。
φ* = 13.91 は14に近いので、t(14)の重みが大きくなります。
実際に計算してみよう
t分布表から値を読み取る
片側検定 α = 0.05 なので、t分布表の「2α = 0.10(両側10%点)」の列を使います。
| 自由度 φ | t(φ, 0.10) |
|---|---|
| 13 | 1.771 |
| 13.91(求めたい) | ? |
| 14 | 1.761 |
重みを計算する
w₁(φ=13側の重み)= (14 − 13.91) / (14 − 13) = 0.09 / 1 = 0.09
w₂(φ=14側の重み)= (13.91 − 13) / (14 − 13) = 0.91 / 1 = 0.91
φ* = 13.91 は14に近いので、φ=14側の重み(0.91)が大きいですね。シーソーのたとえ通りです!
t臨界値を計算する
t(13.91, 0.10) = 0.09 × 1.771 + 0.91 × 1.761
= 0.159 + 1.603
t(13.91, 0.10) = 1.762
Step7:判定する
いよいよ最後のステップです。計算した t₀ と t臨界値を比較します。
判定基準
- t₀ > t(φ*, 2α) → 有意である(帰無仮説を棄却)
- t₀ ≤ t(φ*, 2α) → 有意でない(帰無仮説を棄却できない)
今回の結果
| 検定統計量 t₀ | 1.069 |
| t臨界値 t(13.91, 0.10) | 1.762 |
t₀ = 1.069 < 1.762 = t臨界値
⇒ 有意でない(帰無仮説を棄却できない)
結論
有意水準5%で検定した結果、A法(従来法)とB法(改善法)の母平均に有意な差があるとは言えません。
確かにサンプル平均ではB法の方が小さかったですが、それは「偶然の範囲内」の差であり、「B法が本当に優れている」と結論づけるには証拠不十分です。
「有意でない」= 「差がない」ではありません。
「差があるとは言い切れない」というのが正確な解釈です。サンプルサイズを増やせば、有意になる可能性もあります。

まとめ:Welchの検定と線形補間法のポイント
最後に、この記事で学んだことを整理しましょう。
Welchの検定の手順まとめ
| Step | やること | 今回の計算結果 |
|---|---|---|
| 1 | 平均と分散を計算 | x̄A=5.00, VA=0.909 x̄B=4.50, VB=1.143 |
| 2 | 等分散性を確認(F検定) | F₀=1.257 < 2.0 → 等分散 |
| 3 | 仮説を設定 | H₀: μA=μB, H₁: μA>μB |
| 4 | Welchのt₀を計算 | t₀ = 1.069 |
| 5 | 等価自由度φ*を計算 | φ* = 13.91 |
| 6 | 線形補間でt臨界値を求める | t(13.91, 0.10) = 1.762 |
| 7 | t₀とt臨界値を比較 | 1.069 < 1.762 → 有意でない |
線形補間法のポイント
- 線形補間 = 「表の隙間を埋める」技術
- φ*に近い方のt値ほど、重みが大きくなる
- 重み w₁ + w₂ = 1 になることを確認すると計算ミスを防げる
- 「シーソーのバランス」でイメージすると忘れにくい
QC検定での出題ポイント
- 等価自由度φ*の計算式は選択肢から選ぶ形式が多い
- 線形補間の重みの計算が問われることがある
- 「t₀ > t臨界値 → 有意」の判定を確実に
- 片側検定と両側検定でt分布表の読み方が変わることに注意
📚 次に読むべき記事
同じ人のビフォー・アフターを比較する「対応のあるt検定」を学びましょう
どの検定を使うべきか迷ったときの判断基準を整理しています
検定・推定を体系的に学びたい方はこちらのロードマップへ

