📝 こんな疑問を持っていませんか?
- 🛒「男性と女性で、選ぶ商品って違うのかな?」
- 🤔「独立性の検定」と「適合度の検定」の違いがわからない…
- 📊クロス集計表を作ったけど、この差は統計的に意味があるの?
- 💭2つの変数に「関連がある」と言えるかどうか、どう判断すればいい?
✨ この記事の結論
独立性の検定は「2つのカテゴリ変数に関連があるか」を確かめる検定です。
クロス集計表を使い、「関係がない場合の期待値」と「実際の値」を比較。
そのズレが「偶然の範囲内か」「統計的に意味のある差か」を判定します。
「うちの店、男性客はAセット、女性客はBセットを選ぶ傾向がある気がする…」
「喫煙者と非喫煙者で、病気のなりやすさって本当に違うの?」
こんな風に、「2つの要因に関係がありそう」と感じることってありますよね。
でも、それが「本当に関係がある」のか、「たまたまそう見えるだけ」なのか、感覚だけでは判断できません。
そんなときに使うのが、「独立性の検定」です。
この記事では、独立性の検定の考え方・計算方法・使いどころを、性別と購買行動など身近な例をたくさん使って、初心者の方でも「なるほど!」とイメージできるように解説していきますね。
目次
🔗 独立性の検定とは?|「2つの変数に関連があるか」を調べる
まずは「独立性の検定ってそもそも何?」というところから、やさしく説明していきます。
🎲 「独立」ってどういう意味?
まず、統計学でいう「独立」の意味を理解しましょう。
📖 「独立」とは?
独立 = 「一方の変数が、もう一方の変数に影響を与えない」こと。
言い換えると、「2つの変数に関連がない」「無関係」という意味です。
具体例で考えてみましょう。
✅ 独立している例
サイコロの目とコインの表裏
サイコロで6が出ても、コインが表になる確率は変わらない。
→ 2つは無関係(独立)
❌ 独立していない例
気温とアイスクリームの売上
気温が高いと、アイスの売上も上がる。
→ 2つには関連がある(独立でない)
独立性の検定は、「2つの変数が独立かどうか(=関連があるかないか)」を統計的に判定する検定なんです。
📊 クロス集計表を使って分析する
独立性の検定では、「クロス集計表(分割表)」を使います。
クロス集計表とは、2つのカテゴリ変数を縦横に並べて、度数をまとめた表のことです。
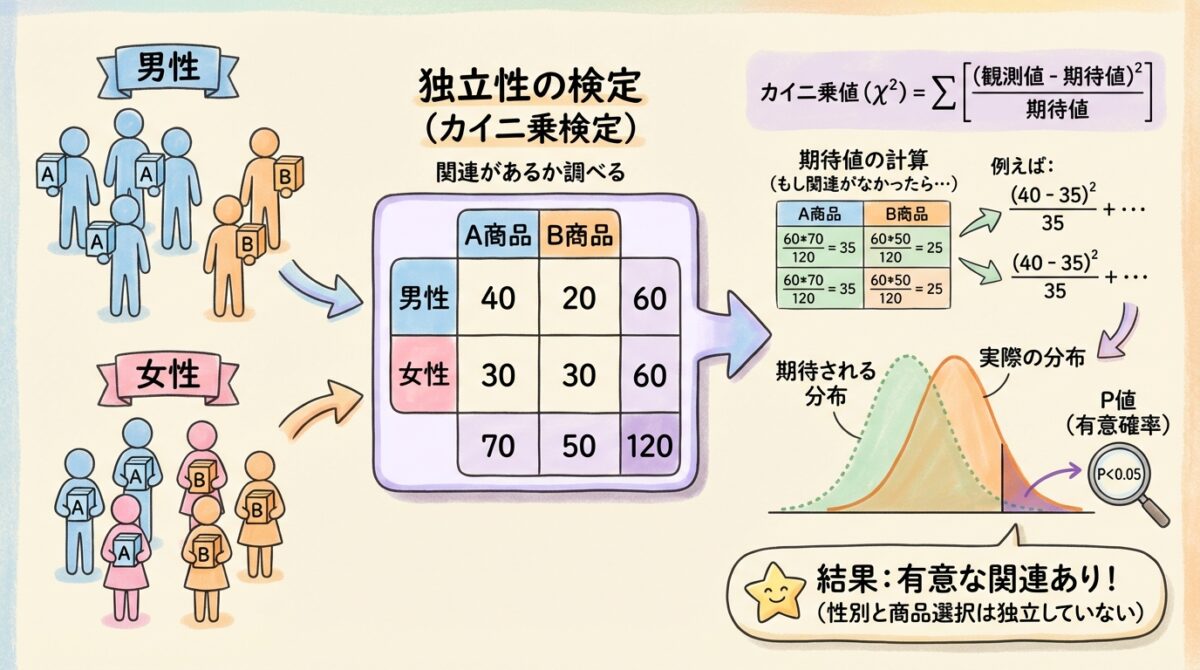
🛒 例:性別と商品選択のクロス集計表
あるカフェで「性別」と「選んだセット(A or B)」を調べました。
🤔 この表を見ると、男性はAセット、女性はBセットを選ぶ傾向がありそう…
でも、これは偶然?それとも本当に関連がある?
🎯 独立性の検定の考え方
独立性の検定は、次のような考え方で進めます。
STEP 1:もし関係がなかったら?を考える
性別と商品選択が完全に独立(無関係)だとしたら、
各セルにはどんな人数が入るはず?(=期待度数を計算)
STEP 2:実際の値とのズレを測る
「期待度数」と「実際の観測度数」のズレを
カイ二乗値(χ²)で数値化する
STEP 3:ズレの大きさを判定
ズレが大きければ → 「関連がある!」
ズレが小さければ → 「関連がない(独立)」
⚖️ 適合度の検定との違い
「カイ二乗検定」には、「適合度の検定」と「独立性の検定」の2種類があります。混同しやすいので、違いを整理しておきましょう。
📊 適合度の検定 vs 独立性の検定
| 適合度の検定 | 独立性の検定 | |
|---|---|---|
| 目的 | データが期待通りの分布に従うか | 2つの変数に関連があるか |
| 変数の数 | 1つのカテゴリ変数 | 2つのカテゴリ変数 |
| 使う表 | 1行の度数表 | クロス集計表(2×2以上) |
| 自由度 | カテゴリ数 − 1 | (行数−1) × (列数−1) |
| 例 | サイコロの各目が均等に出るか | 性別と商品選択に関連があるか |
💡 覚え方のコツ
適合度の検定:「1つの変数」が理論通りか?(分布のチェック)
独立性の検定:「2つの変数」に関係があるか?(関連のチェック)

📋 独立性の検定の仮説|「関係がない」を疑う
独立性の検定でも、まず「仮説」を立てます。どんな仮説になるか見てみましょう。
📋 帰無仮説と対立仮説
H₀:帰無仮説(きむかせつ)
「2つの変数は独立である(関連がない)」
例:「性別と商品選択には関連がない」
=男性も女性も同じ割合でA・Bを選ぶ
H₁:対立仮説(たいりつかせつ)
「2つの変数は独立ではない(関連がある)」
例:「性別と商品選択には関連がある」
=性別によって選ぶ商品の傾向が異なる
📊 クロス集計表の見方を確認
独立性の検定ではクロス集計表を使います。各部分の名前を確認しておきましょう。
📊 クロス集計表の構造
| Aセット | Bセット | 行合計 | |
|---|---|---|---|
| 男性 | O₁₁ = 40 | O₁₂ = 20 | 60 |
| 女性 | O₂₁ = 30 | O₂₂ = 30 | 60 |
| 列合計 | 70 | 50 | 120 |
🧮 期待度数の計算方法
独立性の検定で最も重要なのが、「期待度数」の計算です。
期待度数とは、「2つの変数が完全に独立(無関係)だったら、各セルに入るはずの人数」のことです。
📐 期待度数の計算式
期待度数 = (行合計 × 列合計) / 総計
この公式、なぜこうなるか説明しますね。
💡 期待度数の考え方
もし性別と商品選択が完全に独立なら、男性も女性も同じ割合でA・Bを選ぶはず。
全体でAセットを選んだ人は 70人/120人 = 58.3%
全体でBセットを選んだ人は 50人/120人 = 41.7%
もし独立なら、男性60人も同じ割合でA・Bを選ぶはず:
・男性でAセット:60人 × 58.3% = 35人
・男性でBセット:60人 × 41.7% = 25人
これを式にすると:(行合計 × 列合計)/ 総計 になるんです!
例:男性×Aセットの期待度数 = (60 × 70) / 120 = 35
📝 期待度数を計算してみよう
先ほどの例で、各セルの期待度数を計算してみましょう。
男性 × Aセット
(60 × 70) / 120 = 35
男性 × Bセット
(60 × 50) / 120 = 25
女性 × Aセット
(60 × 70) / 120 = 35
女性 × Bセット
(60 × 50) / 120 = 25
📊 観測度数(実際の値)
| A | B | |
|---|---|---|
| 男性 | 40 | 20 |
| 女性 | 30 | 30 |
📊 期待度数(独立の場合)
| A | B | |
|---|---|---|
| 男性 | 35 | 25 |
| 女性 | 35 | 25 |
見比べてみると、観測度数と期待度数にズレがあることがわかりますね。男性は実際には40人がAを選んでいますが、独立なら35人のはず。このズレが「偶然の範囲内か」を検定で判断します。

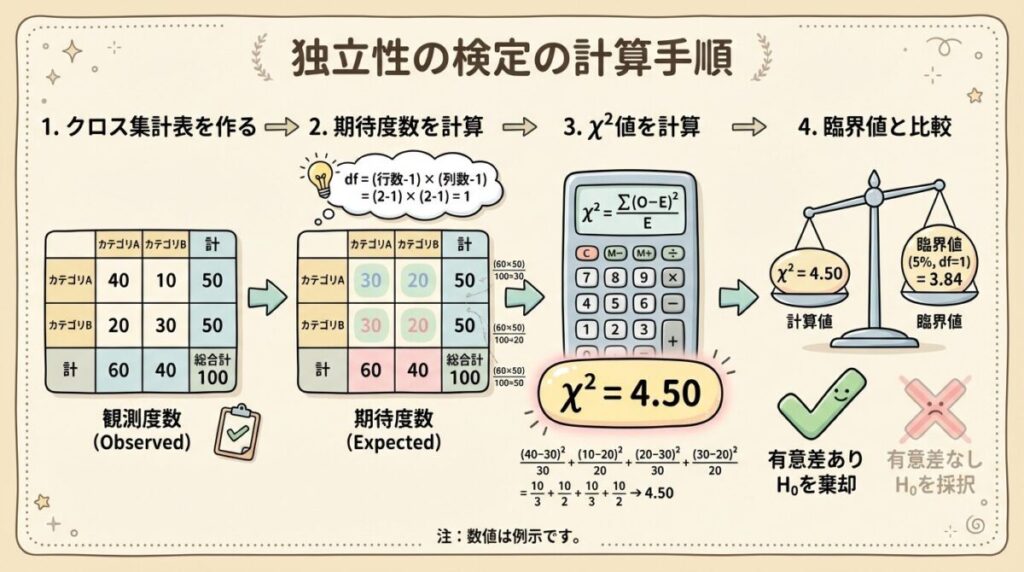
📝 独立性の検定の計算手順|4ステップで完全理解
では、実際の計算手順をステップバイステップで解説していきます。
🛒 例題:性別と商品選択に関連はある?
あるカフェで120人の客を調査したところ、次の結果が得られました。
性別と商品選択に関連があると言えるでしょうか?(有意水準5%で検定)
Step 1:期待度数を計算する
まず、各セルの期待度数を計算します(前のセクションで計算済み)。
期待度数の表
| Aセット | Bセット | |
|---|---|---|
| 男性 | E₁₁ = 35 | E₁₂ = 25 |
| 女性 | E₂₁ = 35 | E₂₂ = 25 |
Step 2:各セルのズレを計算する
各セルについて「(観測度数 − 期待度数)² / 期待度数」を計算します。
| セル | O(観測) | E(期待) | O − E | (O − E)² | (O − E)² / E |
|---|---|---|---|---|---|
| 男性×A | 40 | 35 | +5 | 25 | 0.714 |
| 男性×B | 20 | 25 | −5 | 25 | 1.000 |
| 女性×A | 30 | 35 | −5 | 25 | 0.714 |
| 女性×B | 30 | 25 | +5 | 25 | 1.000 |
Step 3:カイ二乗値(χ²)を計算する
各セルの値をすべて合計してカイ二乗値を求めます。
📐 カイ二乗値の計算式
χ² = Σ (O − E)² / E
χ² = 0.714 + 1.000 + 0.714 + 1.000
χ² = 3.428
Step 4:自由度を求め、臨界値と比較する
独立性の検定の自由度は、次の式で求めます。
自由度 = (行数 − 1) × (列数 − 1)
= (2 − 1) × (2 − 1) = 1 × 1 = 1
有意水準5%、自由度1のカイ二乗分布の臨界値は3.841です。
🎯 判定
計算したχ²値
3.428
臨界値(α=0.05, df=1)
3.841
χ² = 3.428 < 臨界値 3.841
→ 帰無仮説を棄却できない
→ 「性別と商品選択に関連がある」とは言えない
今回のデータでは、男性がAセットを選ぶ傾向は見られましたが、統計的に有意な差とは言えませんでした。このズレは「偶然の範囲内」と判断されます。
💡 実務でのポイント
χ² = 3.428 は臨界値 3.841 にかなり近いですね。
サンプル数を増やして再調査すれば、有意な結果が得られる可能性があります。
「有意でない」は「関連がない」という証明ではなく、「関連があるとは言い切れない」という意味です。

🏭 実践例|製造ラインと不良品の関連を検定してみよう
もう一つ、品質管理の現場で使える実践例を見てみましょう。今度は関連があるパターンです。
🏭 例題:製造ラインと不良発生に関連はある?
工場に3つの製造ラインがあり、それぞれで良品・不良品の数を調べました。
製造ラインと不良発生に関連があると言えるでしょうか?(有意水準5%で検定)
📝 計算してみよう
期待度数を計算します。全体の不良率は 120/600 = 20% です。
期待度数の計算例
カイ二乗値の計算
| セル | O | E | O − E | (O − E)² | (O − E)² / E |
|---|---|---|---|---|---|
| A×良品 | 180 | 160 | +20 | 400 | 2.50 |
| A×不良 | 20 | 40 | −20 | 400 | 10.00 |
| B×良品 | 160 | 160 | 0 | 0 | 0.00 |
| B×不良 | 40 | 40 | 0 | 0 | 0.00 |
| C×良品 | 140 | 160 | −20 | 400 | 2.50 |
| C×不良 | 60 | 40 | +20 | 400 | 10.00 |
| 合計(χ²) | 25.00 | ||||
🎯 判定
自由度 = (3 − 1) × (2 − 1) = 2 × 1 = 2
有意水準5%、自由度2の臨界値 = 5.991
🎯 判定結果
計算したχ²値
25.00
臨界値(α=0.05, df=2)
5.991
χ² = 25.00 > 臨界値 5.991
→ 帰無仮説を棄却!
→ 「製造ラインと不良発生に関連がある」と言える!
製造ラインによって不良率に統計的に有意な差があることがわかりました。データを見ると、ラインAは不良が少なく、ラインCは不良が多いことがわかります。ラインCの設備や作業手順を調査する必要がありそうですね。
🎯 独立性の検定はこんな場面で使える!
独立性の検定は、「2つのカテゴリ変数に関連があるか」を調べたいあらゆる場面で使えます。
🛒
マーケティング分析
性別・年代・地域と購買行動の関連
広告接触と購入の関連
🏭
品質管理
製造ライン・シフト・作業者と不良発生の関連
原材料ロットと品質の関連
🏥
医学・疫学研究
喫煙・生活習慣と疾患の関連
治療法と回復状況の関連
📊
アンケート分析
属性と回答傾向の関連
満足度と再購入意向の関連
🗳️
社会調査
地域・年代と政党支持の関連
学歴と職業の関連
🎓
教育研究
学習方法と成績の関連
出席状況と合格率の関連
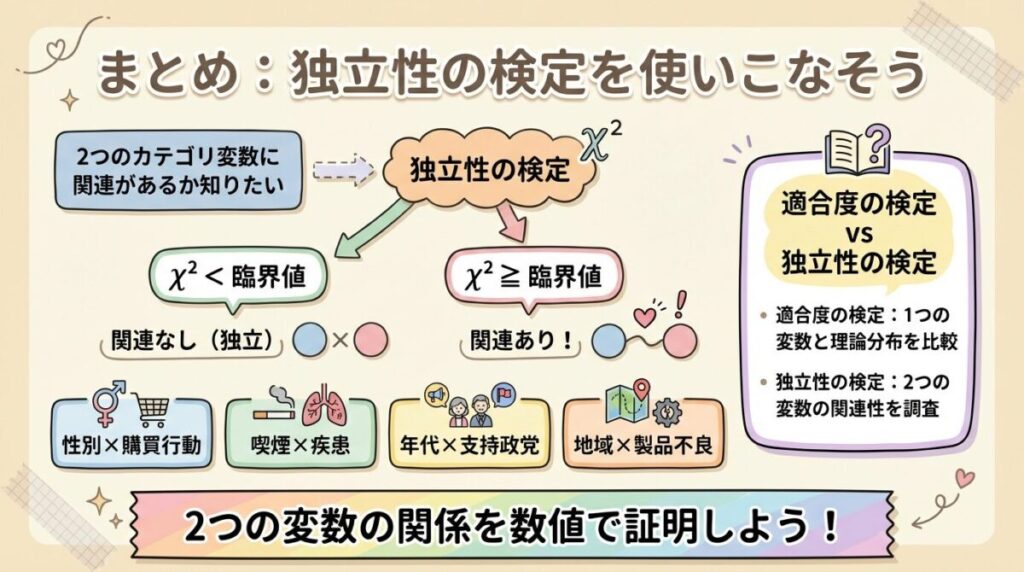
📝 まとめ|独立性の検定を使いこなそう
最後に、この記事のポイントをまとめます。
✅ この記事のまとめ
1. 独立性の検定とは:2つのカテゴリ変数に「関連があるか」を検定する方法。カイ二乗検定の一種。
2. クロス集計表:2つの変数を縦横に並べた表。期待度数 = (行合計 × 列合計) / 総計
3. 計算式:χ² = Σ(O − E)² / E (すべてのセルについて合計)
4. 自由度:(行数 − 1) × (列数 − 1)
5. 判定:χ² ≥ 臨界値 なら「関連あり」、χ² < 臨界値 なら「関連なし(独立)」
🎯 適合度の検定 vs 独立性の検定|使い分け早見表
| 知りたいこと | 使う検定 | 例 |
|---|---|---|
| データが期待通りの分布か? | 適合度の検定 | サイコロの各目は均等に出るか |
| 2つの変数に関連があるか? | 独立性の検定 | 性別と商品選択に関連があるか |
⚠️ 使用上の注意点
- 期待度数は5以上が目安:期待度数が5未満のセルがあると、検定の精度が落ちます(フィッシャーの正確確率検定を検討)
- カテゴリデータ専用:連続データ(身長、売上金額など)には直接使えません
- 関連の強さは別途分析:独立性の検定は「関連があるか」を判定するだけ。関連の強さを知りたい場合は「クラメールのV」などを使用
- 因果関係は示せない:「関連がある」≠「原因と結果」です。因果関係の証明には別の分析が必要
独立性の検定は、「2つの変数に関係がありそう…」という仮説を統計的に検証できる強力なツールです。マーケティング、品質管理、医学研究など、幅広い分野で活用されています。
QC検定でもよく出題されるテーマですので、適合度の検定とセットでしっかりマスターしておいてくださいね。
📚 次に読むべき記事
🔗 セットで学ぼう
【完全図解】適合度の検定とは?|サイコロは本当に公平?を統計で確かめる方法
独立性の検定が「2つの変数の関連」を見るのに対し、適合度の検定は「1つの変数の分布」を見ます。カイ二乗検定の2つの顔を理解しましょう。
📊 ノンパラメトリック検定を学びたい方へ
【完全図解】ウィルコクソンの順位検定とは?|順位で比較するノンパラメトリック検定
カイ二乗検定と並ぶノンパラメトリック検定の代表格。正規分布を仮定しない検定手法をマスターしましょう。