😣 こんな悩みはありませんか？
- 回帰分析の公式が多すぎて、どれを覚えればいいかわからない…
- 公式は知ってるけど、「なぜその式なのか」が理解できない
- 単回帰と重回帰で、どの公式が共通でどこが違うの？
- 検定や推定の公式が似ていて混乱する…
- 回帰分析で覚えるべき公式の全体像と優先順位
- 各公式の「意味」と「使いどころ」
- 単回帰・重回帰の公式の共通点と違い
- 関連記事への学習ロードマップ
回帰分析を学んでいると、次々と新しい公式が出てきて混乱しますよね。
「傾きの公式」「決定係数の公式」「検定統計量の公式」…。似たような記号が並び、どれがどれだかわからなくなってしまいます。
この記事では、回帰分析・重回帰分析で本当に覚えるべき公式を一覧表にまとめ、それぞれの「意味」と「使いどころ」を整理しました。
公式を「丸暗記」するのではなく、「なぜこうなるのか」を理解するための入口として、この記事を活用してください。
💡 この記事の使い方
まず一覧表で全体像を把握し、詳しく知りたい公式は関連記事リンクから深掘りしてください。ブックマーク推奨です！
まず一覧表で全体像を把握し、詳しく知りたい公式は関連記事リンクから深掘りしてください。ブックマーク推奨です！
目次
【保存版】回帰分析 公式一覧表
まずは、回帰分析で覚えるべき公式の全体像を一覧表で確認しましょう。
公式は5つのカテゴリに分類しています。上から順に学習することをおすすめします。
カテゴリ①：単回帰の基本式
| 公式名 | 公式 | 意味 | 関連記事 |
|---|---|---|---|
| 回帰直線 | ŷ = a + bx | xからyを予測する直線 | 詳細 → |
| 傾き b | b = Sxy / Sxx | xが1増えるとyがb増える | 詳細 → |
| 切片 a | a = ȳ − b x̄ | x=0のときのyの値 | 詳細 → |
| 残差 | eᵢ = yᵢ − ŷᵢ | 実測値と予測値のズレ | 詳細 → |
📐 記号の意味
• Sxy：xとyの偏差積和 = Σ(xᵢ − x̄)(yᵢ − ȳ)
• Sxx：xの偏差平方和 = Σ(xᵢ − x̄)²
• x̄, ȳ：x, yの平均値
• Sxy：xとyの偏差積和 = Σ(xᵢ − x̄)(yᵢ − ȳ)
• Sxx：xの偏差平方和 = Σ(xᵢ − x̄)²
• x̄, ȳ：x, yの平均値
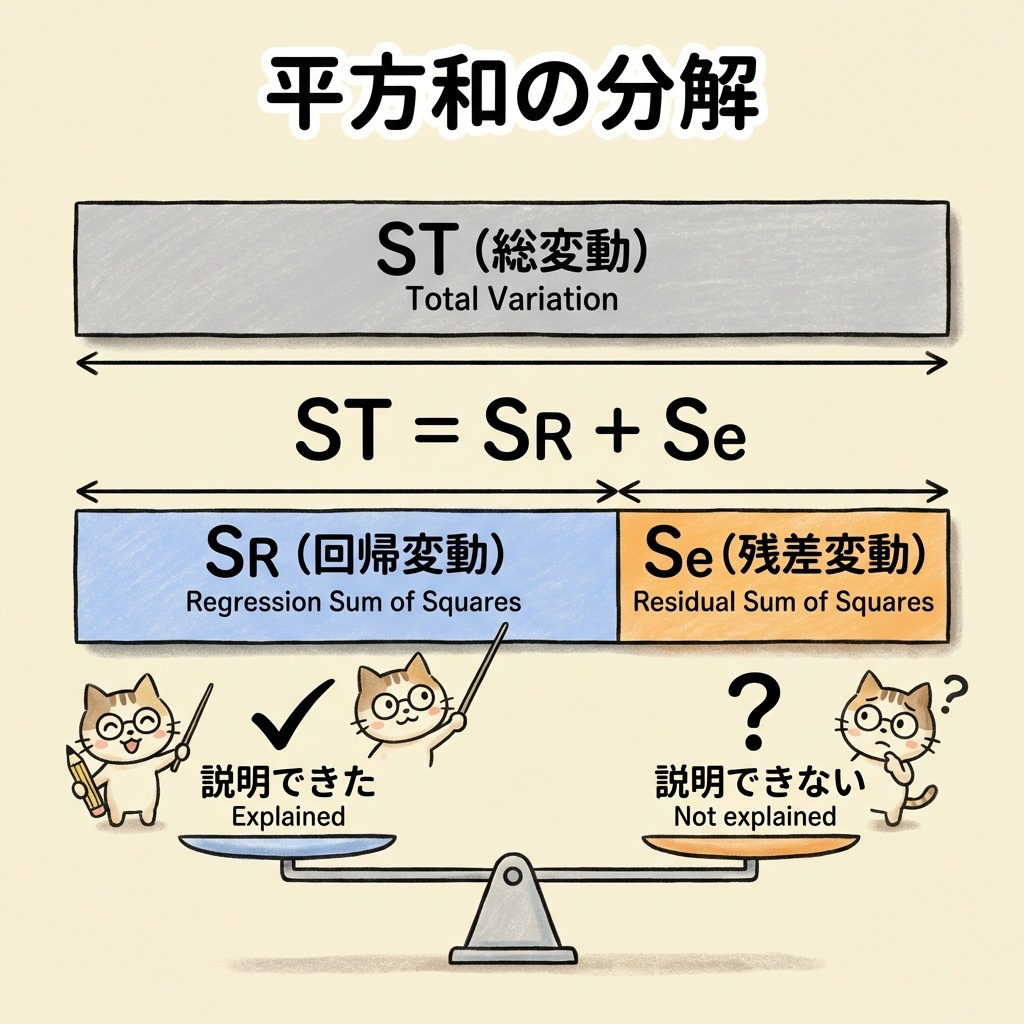
カテゴリ②：平方和の分解
| 公式名 | 公式 | 意味 | 関連記事 |
|---|---|---|---|
| 総平方和 ST | ST = Σ(yᵢ − ȳ)² | yの全体のバラつき | 詳細 → |
| 回帰平方和 SR | SR = Σ(ŷᵢ − ȳ)² | 回帰で説明できたバラつき | 詳細 → |
| 残差平方和 Se | Se = Σ(yᵢ − ŷᵢ)² | 回帰で説明できないバラつき | 詳細 → |
| 分解の関係 | ST = SR + Se | 全体 = 説明 + 残差 | 詳細 → |
カテゴリ③：相関と決定係数
| 公式名 | 公式 | 意味 | 関連記事 |
|---|---|---|---|
| 相関係数 r | r = Sxy / √(Sxx・Syy) | xとyの直線関係の強さ（−1〜+1） | 詳細 → |
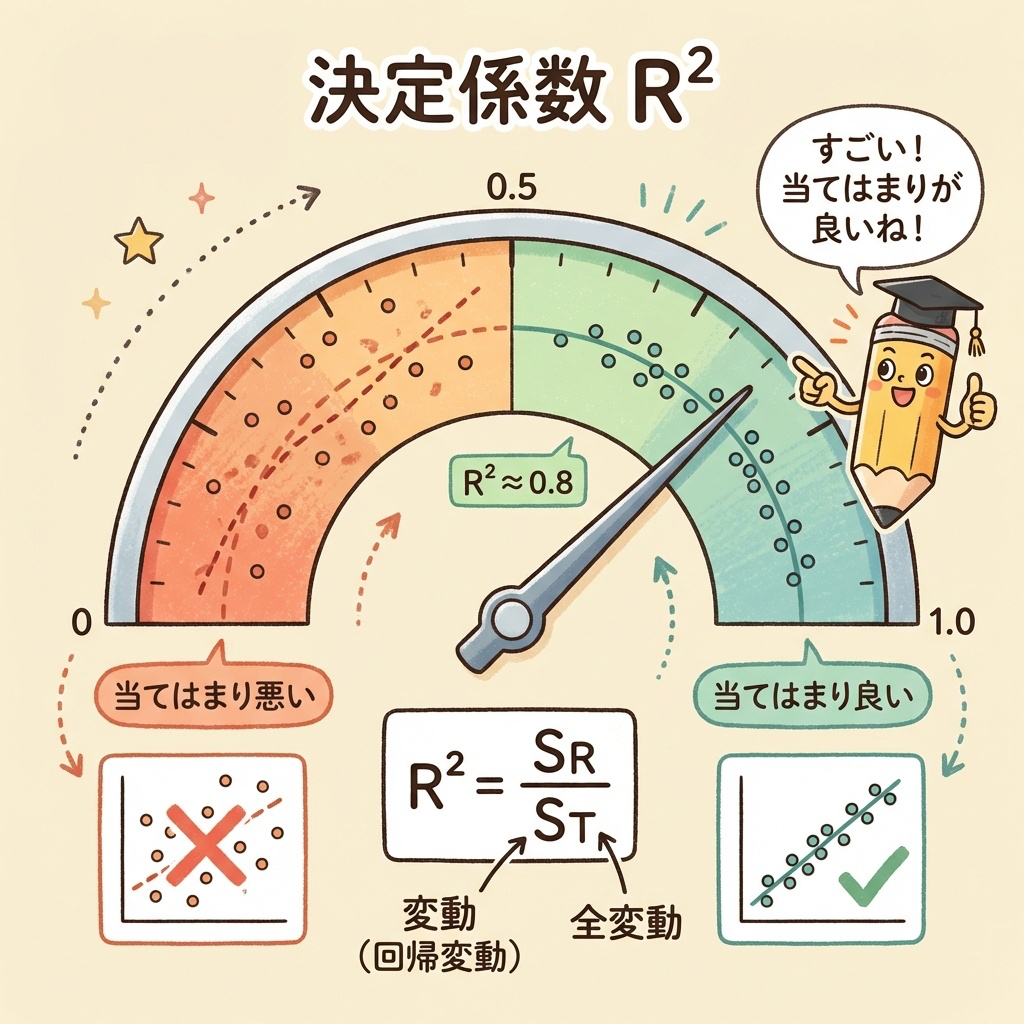
| 決定係数 R² | R² = SR / ST = 1 − Se/ST | 回帰で説明できる割合（0〜1） | 詳細 → |
| r と R² の関係 | R² = r²（単回帰のみ） | 単回帰では相関係数の2乗が決定係数 | 詳細 → |
| 寄与率 | R² × 100 (%) | 決定係数を%で表現 | 詳細 → |
💡 覚え方のコツ
R² = 0.64 なら「このモデルはyのバラつきの64%を説明できている」と解釈します。残り36%は説明できない部分（残差）です。
R² = 0.64 なら「このモデルはyのバラつきの64%を説明できている」と解釈します。残り36%は説明できない部分（残差）です。
カテゴリ④：検定統計量
| 公式名 | 公式 | 用途 | 関連記事 |
|---|---|---|---|
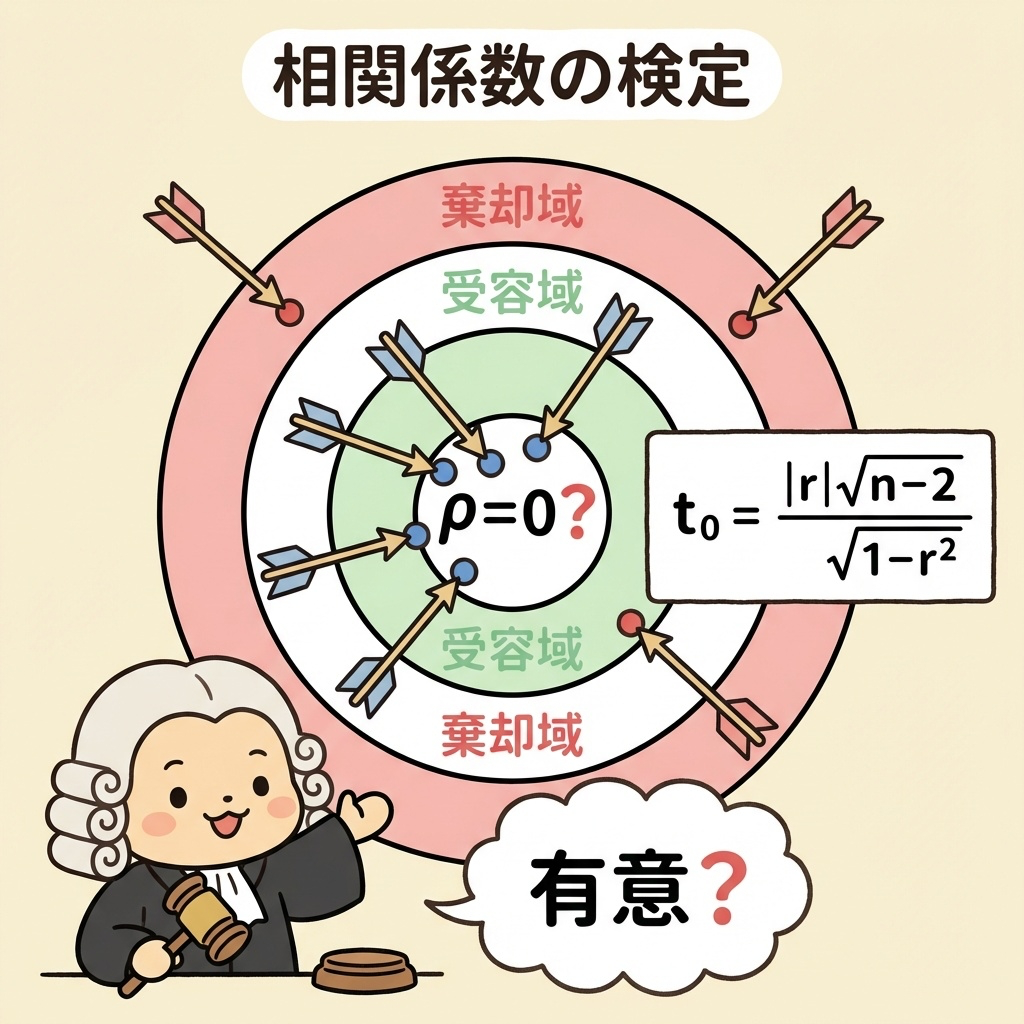
| 相関係数の検定 | t₀ = |r|√(n−2) / √(1−r²) | 相関が偶然かどうか検定 | 詳細 → |
| 回帰係数の検定 | t₀ = b / SE(b) | 傾きが0でないか検定 | 詳細 → |
| 回帰の有意性検定（F検定） | F₀ = VR / Ve | モデル全体が有意か検定 | 詳細 → |
📐 相関係数の検定式の覚え方
分母：相関で説明できない不確かさ √(1−r²)
→ 「シグナル ÷ ノイズ」の構造
t₀ =
分子：相関の強さ |r| × サンプルサイズの効果 √(n−2)|r| × √(n − 2)
√(1 − r²)
分母：相関で説明できない不確かさ √(1−r²)
→ 「シグナル ÷ ノイズ」の構造
カテゴリ⑤：区間推定
| 公式名 | 公式 | 用途 | 関連記事 |
|---|---|---|---|
| 回帰係数bの区間推定 | b ± t(α/2, n−2) × SE(b) | 傾きの95%信頼区間 | 詳細 → |
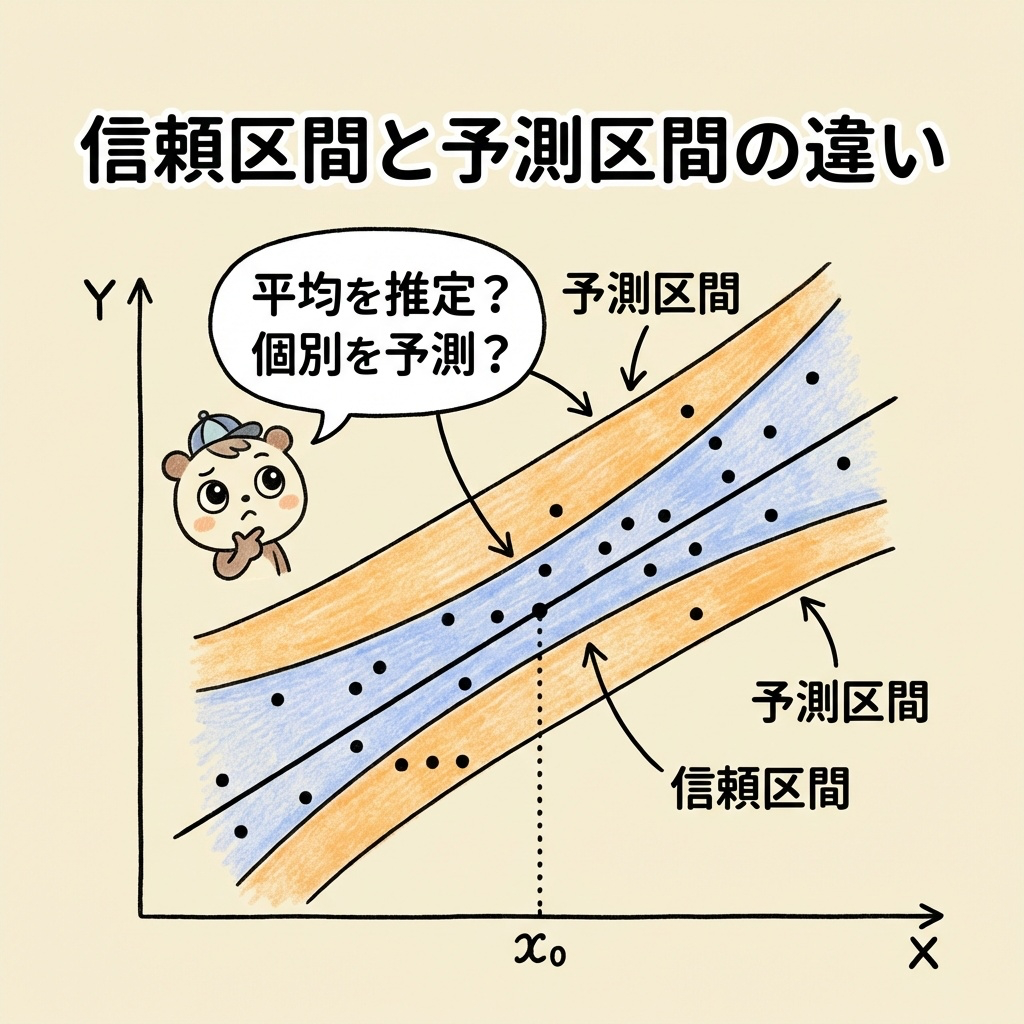
| 信頼区間（平均の推定） | ŷ₀ ± t × √[Ve(1/n + (x₀−x̄)²/Sxx)] | x₀における平均yの区間 | 詳細 → |
| 予測区間（個別の推定） | ŷ₀ ± t × √[Ve(1 + 1/n + (x₀−x̄)²/Sxx)] | x₀における個別yの区間 | 詳細 → |
| 相関係数の区間推定 | フィッシャーのz変換を使用 | rの95%信頼区間 | 詳細 → |
⚠️ 信頼区間と予測区間の違いに注意
• 信頼区間：「x₀のときの平均的なyはどの範囲か？」
• 予測区間：「x₀のときの個別のyはどの範囲か？」
→ 予測区間の方が必ず広くなります（個別のバラつきを考慮するため）
• 信頼区間：「x₀のときの平均的なyはどの範囲か？」
• 予測区間：「x₀のときの個別のyはどの範囲か？」
→ 予測区間の方が必ず広くなります（個別のバラつきを考慮するため）
【保存版】重回帰分析 公式一覧表
続いて、重回帰分析で追加される公式を見ていきましょう。
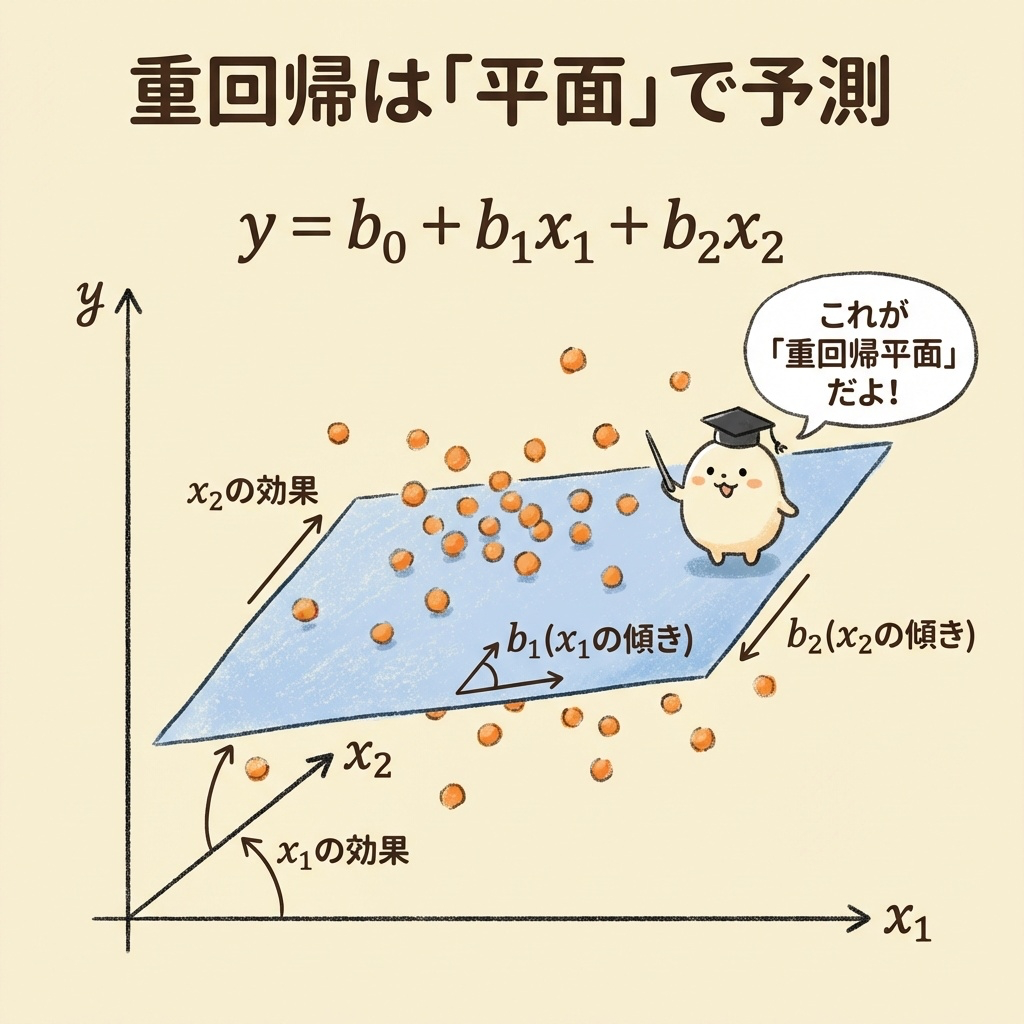
単回帰との違いは、説明変数が2つ以上になることです。直線ではなく「平面」や「超平面」でyを予測します。
重回帰の基本式
| 公式名 | 公式 | 意味 | 関連記事 |
|---|---|---|---|
| 重回帰式 | ŷ = b₀ + b₁x₁ + b₂x₂ + … | 複数のxからyを予測 | 詳細 → |
| 偏回帰係数 bⱼ | 正規方程式から算出 | 他のxを固定したときのxⱼの効果 | 詳細 → |
| 正規方程式 | (X'X)b = X'y | 偏回帰係数を求める連立方程式 | 詳細 → |
💡 偏回帰係数の意味
偏回帰係数 b₁ は「x₂を固定したとき、x₁が1増えるとyがb₁増える」という意味です。単回帰の傾きとは違い、「他の変数の影響を取り除いた純粋な効果」を表します。
偏回帰係数 b₁ は「x₂を固定したとき、x₁が1増えるとyがb₁増える」という意味です。単回帰の傾きとは違い、「他の変数の影響を取り除いた純粋な効果」を表します。
重回帰の検定・評価
| 公式名 | 公式 | 意味 | 関連記事 |
|---|---|---|---|
| 自由度調整済み R² | R²* = 1 − (1−R²)(n−1)/(n−k−1) | 変数の数で調整した決定係数 | 詳細 → |
| モデル全体のF検定 | F₀ = (SR/k) / (Se/(n−k−1)) | モデル全体が有意か | 詳細 → |
| 偏回帰係数のt検定 | t₀ = bⱼ / SE(bⱼ) | 各変数が有意か | 詳細 → |
| VIF（分散拡大係数） | VIF = 1 / (1 − Rⱼ²) | 多重共線性の指標 | 詳細 → |
⚠️ 重回帰の注意点：多重共線性
説明変数同士に強い相関があると、偏回帰係数が不安定になります。VIF > 10 なら多重共線性の疑いがあります。どちらかの変数を削除するなどの対策が必要です。
説明変数同士に強い相関があると、偏回帰係数が不安定になります。VIF > 10 なら多重共線性の疑いがあります。どちらかの変数を削除するなどの対策が必要です。
単回帰と重回帰の公式比較
単回帰と重回帰では、考え方は同じで、式の形が拡張される関係にあります。対比表で整理しましょう。
| 項目 | 単回帰 | 重回帰 |
|---|---|---|
| モデル式 | ŷ = a + bx | ŷ = b₀ + b₁x₁ + b₂x₂ + … |
| 予測の形 | 直線 | 平面（超平面） |
| 回帰係数の意味 | xが1増えるとyがb増える | 他を固定してxⱼが1増えるとyがbⱼ増える |
| 決定係数 | R² = r² | R²（r²とは一致しない） |
| 回帰の自由度 | 1 | k（説明変数の数） |
| 残差の自由度 | n − 2 | n − k − 1 |
| 注意点 | − | 多重共線性に注意 |
💡 ポイント
重回帰の自由度は「n − k − 1」です。データ数 n から、推定するパラメータ数（k個の偏回帰係数 + 1個の切片）を引きます。単回帰（k=1）なら n−1−1 = n−2 となり、単回帰の公式と一致します。
重回帰の自由度は「n − k − 1」です。データ数 n から、推定するパラメータ数（k個の偏回帰係数 + 1個の切片）を引きます。単回帰（k=1）なら n−1−1 = n−2 となり、単回帰の公式と一致します。
公式の学習ロードマップ
公式を効率的に学ぶには、順序が大切です。以下のロードマップに沿って学習することをおすすめします。
Step 1：回帰分析の基礎を理解する
| 順序 | 学習内容 | 関連記事 |
|---|---|---|
| 1 | 回帰分析とは何か？（全体像の把握） | 記事を読む → |
| 2 | 相関と回帰の違い | 記事を読む → |
| 3 | 最小二乗法のしくみ | 記事を読む → |
| 4 | 残差と誤差の違い | 記事を読む → |
Step 2：評価指標を理解する
| 順序 | 学習内容 | 関連記事 |
|---|---|---|
| 5 | 決定係数 R² の意味 | 記事を読む → |
| 6 | r と R² の関係 | 記事を読む → |
| 7 | 寄与率の計算 | 記事を読む → |
Step 3：検定・推定を学ぶ
| 順序 | 学習内容 | 関連記事 |
|---|---|---|
| 8 | 回帰係数の検定（t検定） | 記事を読む → |
| 9 | 回帰の前提条件 | 記事を読む → |
| 10 | 信頼区間と予測区間 | 記事を読む → |
Step 4：重回帰に進む
| 順序 | 学習内容 | 関連記事 |
|---|---|---|
| 11 | 重回帰分析とは？ | 記事を読む → |
| 12 | 偏回帰係数の意味 | 記事を読む → |
| 13 | 多重共線性（VIF） | 記事を読む → |
| 14 | 変数選択の方法 | 記事を読む → |
📘 回帰分析の全体像を把握するなら
【完全版】回帰分析の学習ロードマップ｜相関分析から重回帰まで体系的にマスター →
【完全版】回帰分析の学習ロードマップ｜相関分析から重回帰まで体系的にマスター →
まとめ｜公式は「意味」で覚える
この記事では、回帰分析・重回帰分析で覚えるべき公式を一覧で整理しました。
📝 この記事のまとめ
- 単回帰の基本式：ŷ = a + bx、傾き b = Sxy/Sxx、切片 a = ȳ − bx̄
- 平方和の分解：ST = SR + Se（全体 = 説明できた + 残差）
- 決定係数：R² = SR/ST（0〜1で「当てはまりの良さ」を表す）
- 相関係数の検定：t₀ = |r|√(n−2) / √(1−r²)
- 重回帰の特徴：偏回帰係数は「他を固定したときの効果」、VIFで多重共線性をチェック
- 信頼区間と予測区間：平均の推定か、個別の推定かで使い分け
公式を丸暗記するのではなく、「この公式は何を計算しているのか」「なぜこの形なのか」を意識すると、忘れにくくなります。
この記事をブックマークして、公式を確認したいときにいつでも戻ってきてください。各公式の詳細は、リンク先の記事で深掘りできます。
💡 最後に
公式を覚えたら、実際に手を動かして計算してみましょう。エクセルやPythonで実データを分析すると、公式の意味がより深く理解できます。
公式を覚えたら、実際に手を動かして計算してみましょう。エクセルやPythonで実データを分析すると、公式の意味がより深く理解できます。
📚 次に読むべき記事
📘 【完全版】回帰分析の学習ロードマップ →
回帰分析の全体像を把握し、体系的に学習を進めたい方はこちら。
📘 【完全版】統計学の勉強ロードマップ →
回帰分析だけでなく、統計学全体を体系的に学びたい方はこちら。
📘 【完全版】検定・推定の学習ロードマップ →
回帰分析の検定をより深く理解するために、検定・推定の基礎を固めたい方はこちら。