- 「データなんて全部数字でしょ?」と思っている
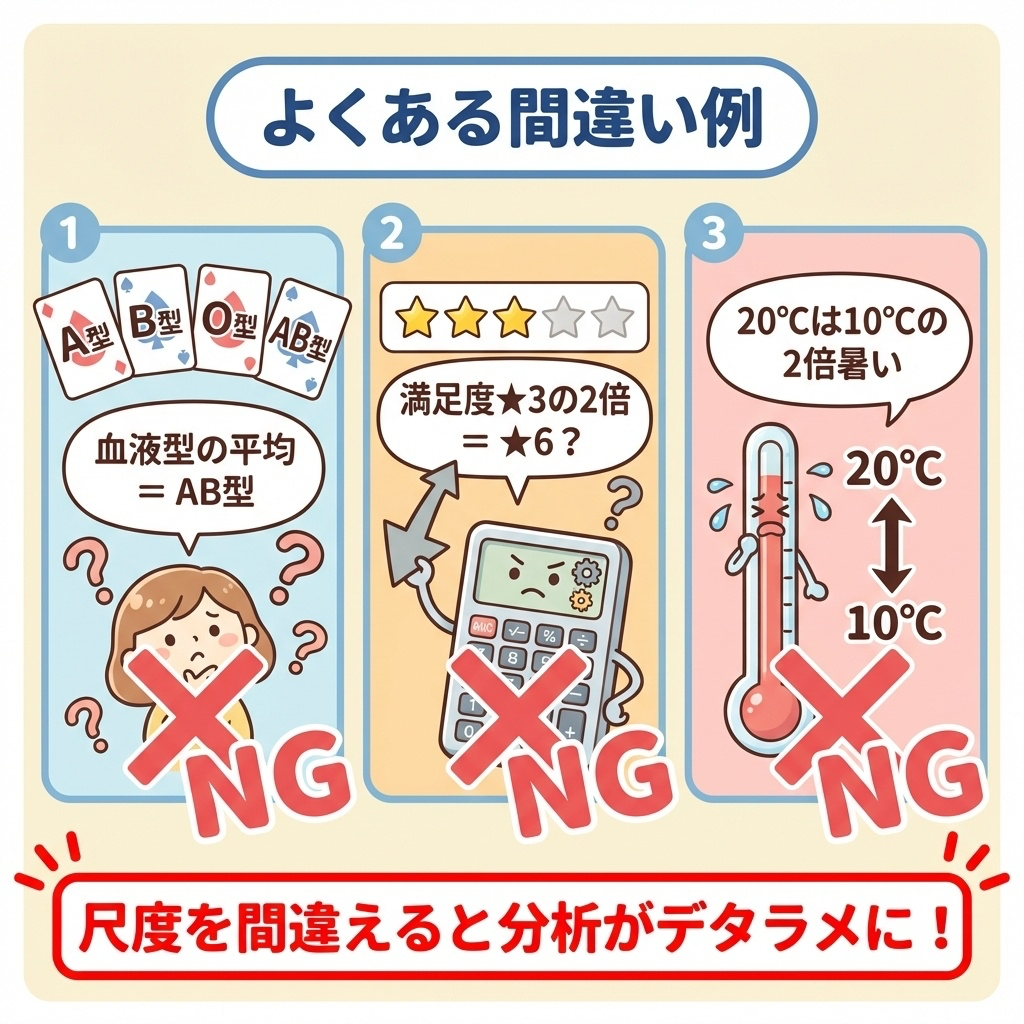
- 血液型の「平均」を計算しようとして怒られた
- 満足度アンケートの「平均3.5点」に違和感がある
- 「気温20℃は10℃の2倍暑い」と言ったら否定された
- データの4つの種類(尺度)を図解で完全理解
- 「何が計算できて、何ができないか」が一目でわかる
- 尺度を間違えると分析が台無しになる理由
- 実践クイズで自分のデータの尺度を判定できるようになる
目次
なぜ「データの種類」を知る必要があるのか?
統計学を学ぶとき、いきなり「平均」や「標準偏差」を計算しようとしていませんか?
実は、その前に絶対に知っておくべきことがあります。それが「データの種類(尺度)」です。
例えば、こんな計算をしようとしていませんか?
「A型の人が5人、B型が3人、O型が2人。平均すると…えーと…」
→ これ、計算できません。
血液型は「ラベル」であって、足したり平均したりする対象ではないからです。
データには4つのタイプ(尺度)があり、タイプによって「できる計算」と「できない計算」が決まっています。
この記事では、その4つの尺度を図解で直感的に理解できるようにします。
データの「4つの尺度」を図解で理解する
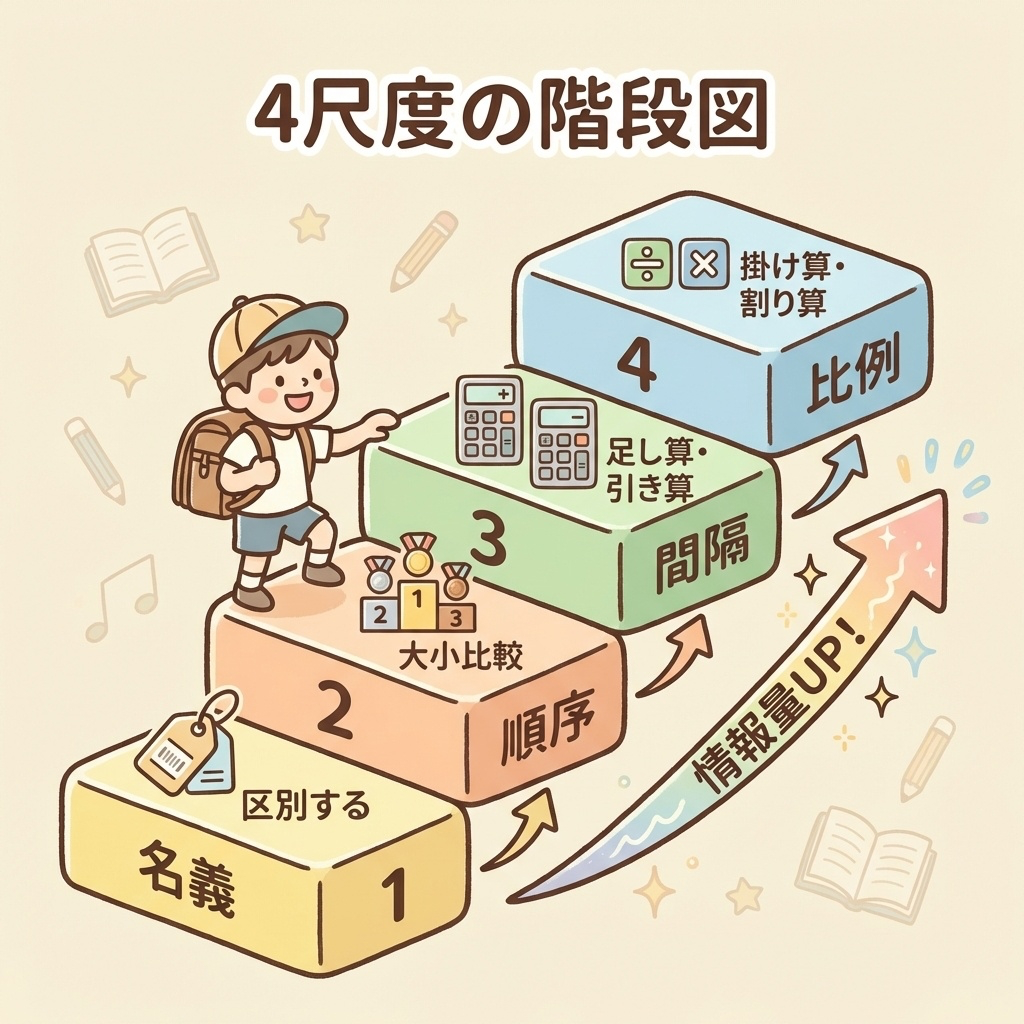
統計学では、データを以下の4つのレベル(尺度)に分類します。
下から上に行くほど「情報量が多く、できる計算が増える」と覚えてください。
| レベル | 尺度 | 一言で言うと | 具体例 |
|---|---|---|---|
| Lv.1 | 名義尺度 | ただのラベル | 血液型、性別、背番号 |
| Lv.2 | 順序尺度 | 順番がわかる | ランキング、満足度★ |
| Lv.3 | 間隔尺度 | 差が等しい | 気温(℃)、西暦、偏差値 |
| Lv.4 | 比例尺度 | 比率が言える(最強) | 身長、体重、金額 |
「名前・順番・間隔・比率」
→「名・順・間・比(めいじゅんかんひ)」と覚えましょう。
下から上に「情報量アップ」のイメージです。
① 名義尺度|ただの「ラベル」で区別するだけ
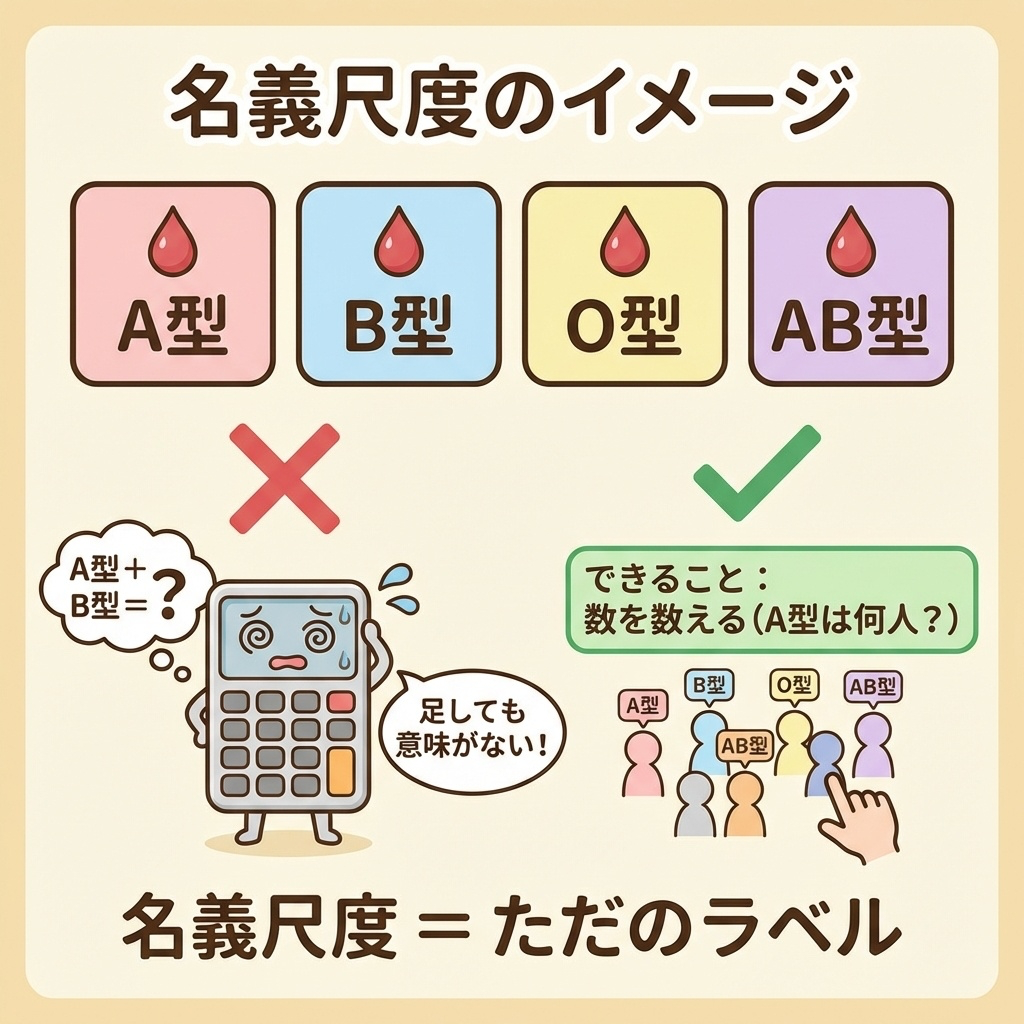
名義尺度は、データを単純に「区別・分類」するためだけのものです。
数字が割り振られていても、その数字に「大きさ」や「順番」の意味はありません。
名義尺度の具体例
| 例 | なぜ名義尺度か? |
|---|---|
| 血液型(A, B, O, AB) | A型がB型より「偉い」わけではない |
| 性別(男性, 女性) | 区別するだけで大小関係がない |
| 背番号(1番, 10番) | 10番が1番の10倍強いわけではない |
| 郵便番号(100-0001) | 数字だけど足しても意味がない |
名義尺度でできること・できないこと
- 個数を数える(A型は何人?)
- 最も多いカテゴリを調べる(最頻値)
- 同じか違うかを判定する
- 足し算・引き算
- 平均値の計算
- 大小比較
「血液型の平均は…AB型!」
→ これは計算できません。血液型は「ラベル」なので、平均という概念がありません。
「A型が10人中4人で最も多い」のように数を数えることだけが許されます。
② 順序尺度|順番はわかるけど「差」は不明
順序尺度は、「順位・ランキング」の大小関係がわかります。
ただし、その間隔(差)が等しいとは限らないのがポイントです。
順序尺度の具体例
| 例 | なぜ順序尺度か? |
|---|---|
| マラソンの順位(1位, 2位, 3位) | 1位と2位の差が0.1秒、2位と3位の差が5秒かもしれない |
| 満足度(★★★★★) | ★3と★4の差 ≠ ★4と★5の差 |
| 企業規模(大・中・小) | 「大」が「中」の何倍かは不明 |
| 学年(1年, 2年, 3年) | 順番はあるが、学力差は等間隔ではない |
順序尺度でできること・できないこと
- 大小比較(1位 > 2位)
- 中央値を求める
- 最頻値を求める
- 足し算・引き算(差に意味がない)
- 厳密な平均値
- 比率の計算
「満足度の平均は3.5点」のように、順序尺度でも平均を計算することがあります。
ただし、厳密には不適切な計算であることを理解した上で使いましょう。
(「★3と★4の差」が「★4と★5の差」と同じとは限らないため)
第4回:中央値と最頻値 - 平均以外の代表値 →

③ 間隔尺度|差は等しいけど「比率」はダメ
間隔尺度は、目盛りの間隔が等しく、「足し算・引き算」に意味があります。
ただし、「ゼロ」が「無」を意味しない(相対的なゼロ)ため、比率の計算はできません。
間隔尺度の具体例
| 例 | なぜ間隔尺度か? |
|---|---|
| 気温(℃) | 0℃は「熱がゼロ」ではない。「20℃は10℃の2倍暑い」とは言えない |
| 西暦(年) | 「西暦0年」は「時間がゼロ」ではない |
| 偏差値・IQ | 偏差値0は「知能ゼロ」ではない |
「今日は20℃で、昨日は10℃だった。今日は昨日の2倍暑い!」
→ これは間違いです。
なぜなら、0℃は「熱エネルギーがゼロ」ではないからです。
(絶対零度-273℃が本当の「熱ゼロ」)
「20℃と10℃の差は10℃」とは言えますが、「2倍」とは言えません。
間隔尺度でできること・できないこと
- 大小比較
- 足し算・引き算
- 平均値の計算
- 標準偏差の計算
- 掛け算・割り算
- 「〇倍」という比率表現
第3回:平均値の奥深い世界 →

④ 比例尺度|全ての計算ができる「最強のデータ」
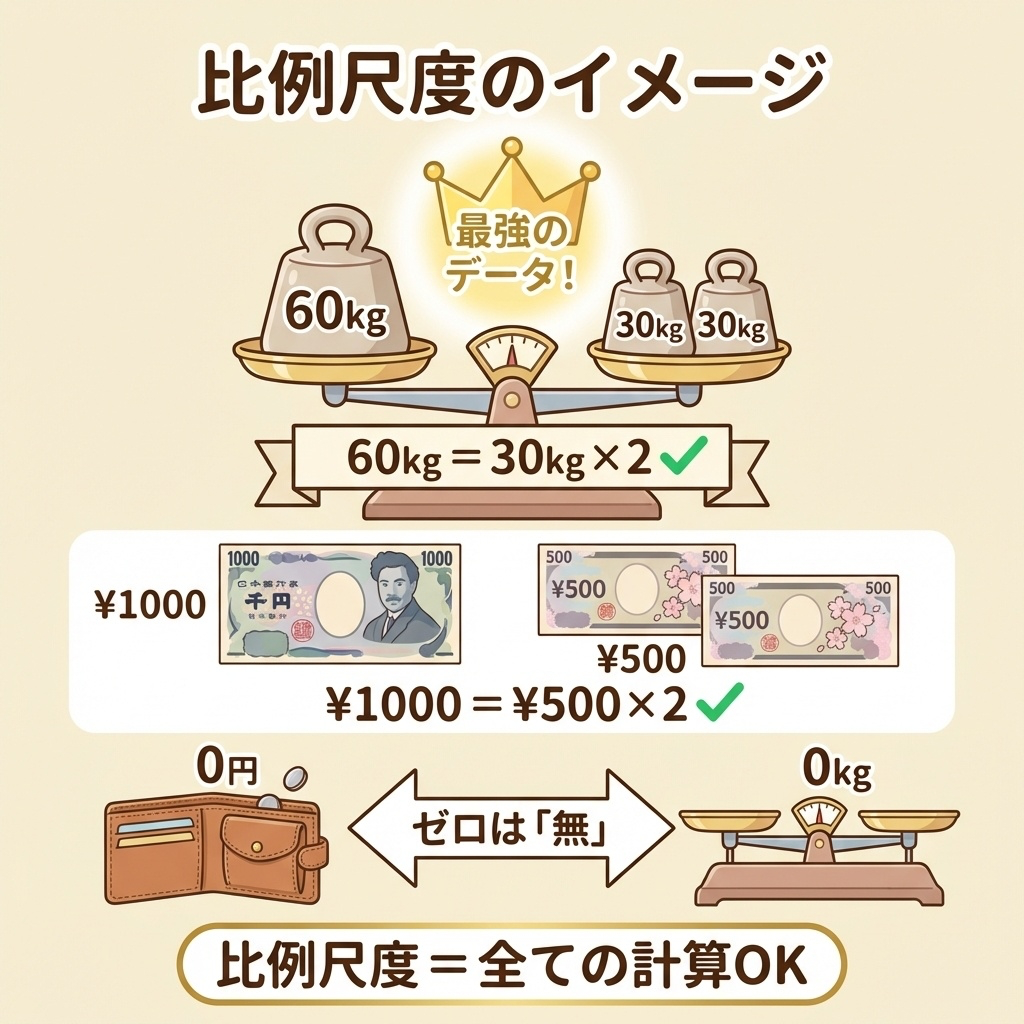
比例尺度は、「絶対的なゼロ(無)」があり、全ての計算が可能です。
「AはBの2倍」といった比率の表現ができるのが最大の特徴です。
比例尺度の具体例
| 例 | なぜ比例尺度か? |
|---|---|
| 身長・体重 | 0kgは「重さゼロ」。60kgは30kgの2倍重い |
| 金額(円) | 0円は「所持金ゼロ」。1000円は500円の2倍 |
| 時間(秒・分) | 0秒は「時間ゼロ」。60分は30分の2倍長い |
| 距離(km) | 0kmは「移動ゼロ」。10kmは5kmの2倍遠い |
比例尺度でできること
- 大小比較(50kg > 30kg)
- 足し算・引き算(50kg − 30kg = 20kg)
- 平均値・標準偏差
- 掛け算・割り算(60kg ÷ 30kg = 2倍)
- 比率の表現(「AはBの2倍」)
比例尺度と間隔尺度の違いは「0が本当の無を意味するか」です。
・0円 = お金がない(本当の無)→ 比例尺度
・0℃ = 熱がない?(いいえ、-273℃が本当の無)→ 間隔尺度
早見表|尺度別「何が計算できるか」
4つの尺度で「使える計算」を一覧表にまとめました。
| 尺度 | 大小 比較 |
足し算 引き算 |
掛け算 割り算 |
平均値 | 代表的な統計手法 |
|---|---|---|---|---|---|
| 名義尺度 | × | × | × | × | 度数、最頻値、カイ二乗検定 |
| 順序尺度 | ○ | × | × | △ | 中央値、順位相関、ノンパラ検定 |
| 間隔尺度 | ○ | ○ | × | ○ | 平均、標準偏差、相関係数 |
| 比例尺度 | ○ | ○ | ○ | ○ | 全ての手法が使用可能 |
※順序尺度の平均値は、厳密には不適切ですが実務では使われることがあります(△)。
【実践】尺度を判定するフローチャート
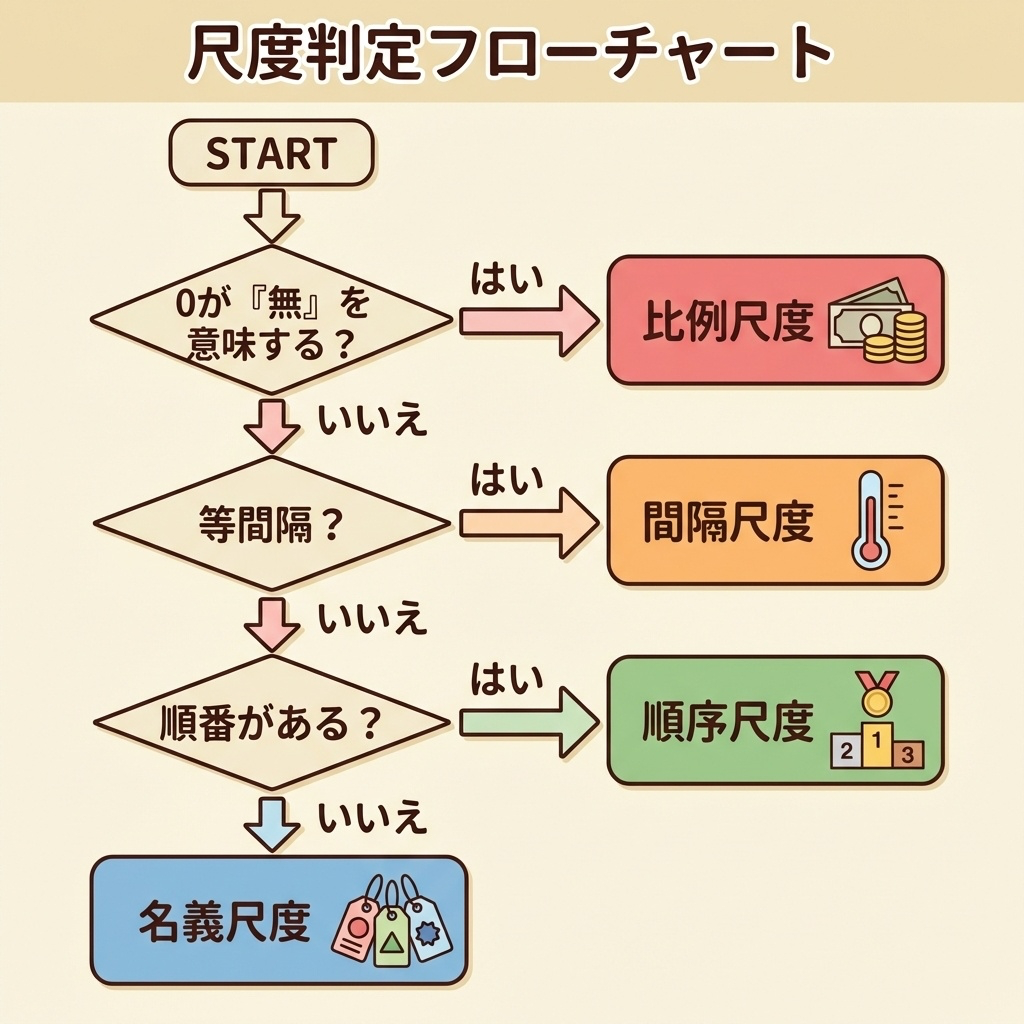
「このデータはどの尺度?」と迷ったら、以下の順番で判定してください。
Q1. 「0」が「無」を意味する?
→ Yes なら 比例尺度
→ No なら Q2へ
Q2. 目盛りが「等間隔」?
→ Yes なら 間隔尺度
→ No なら Q3へ
Q3. 「順番」がある?
→ Yes なら 順序尺度
→ No なら 名義尺度
実践クイズ|あなたは正しく判定できる?
理解度チェックです。以下のデータはどの尺度でしょうか?
Q1. 郵便番号(100-0001)
答えを見る
答え:名義尺度
数字ですが、ただの「ラベル」です。100-0001と100-0002を足しても意味がありません。
Q2. マラソンの順位(1位、2位、3位…)
答えを見る
答え:順序尺度
順番に意味がありますが、1位と2位の差(タイム差)は等間隔ではありません。
Q3. 気温(25℃)
答えを見る
答え:間隔尺度
0℃は「熱エネルギーがゼロ」ではないので、「2倍暑い」とは言えません。
Q4. 年収(500万円)
答えを見る
答え:比例尺度
0円は「所得ゼロ」という本当の無です。「1000万は500万の2倍」と言えます。
Q5. 偏差値(55)
答えを見る
答え:間隔尺度
偏差値0は「能力ゼロ」ではありません。平均を50とした相対的な数値です。
まとめ|この記事のポイント
- 名義尺度:区別するだけ(血液型、性別)→ 数を数えるだけ
- 順序尺度:大小関係あり(ランキング)→ 中央値まで
- 間隔尺度:差が等しい(気温、偏差値)→ 平均まで
- 比例尺度:比率が言える(身長、金額)→ 全ての計算OK
「0が本当の無を意味するか?」を最初に考えましょう。
Yes → 比例尺度(最強)
No → 間隔尺度以下
📚 次に読むべき記事
算術平均・幾何平均・調和平均の違いを学ぶ
順序尺度でも使える「中央値」をマスター
間隔尺度以上で使える「バラつき」の指標
間隔・比例尺度のデータを可視化する方法
尺度に応じた検定手法の選び方を学ぶ