😰 こんな悩み、ありませんか?
- インピーダンスって結局なんなの?
- なぜ単純にR + XL + XCじゃダメなの?
- √の中に2乗が出てくる理由がわからない
- XL - XCの「引き算」がピンとこない
📌 この記事の結論
インピーダンスは「交流における電流の流れにくさ」。R・XL・XCは向きが違うので、単純に足せません。ベクトルの合成として三平方の定理で計算するのがポイントです!
インピーダンス(Z)は、電験三種の理論科目で最重要テーマの一つです。
交流回路の計算問題は、ほぼすべてインピーダンスの理解が前提になっています。
でも、「なぜルートの中に2乗があるの?」「なぜ引き算するの?」と疑問に思う方も多いはず。
この記事では、「なぜそうなるのか」をイメージで理解できるように解説します。公式を丸暗記するのではなく、図で考える力を身につけましょう!
目次
⚡ インピーダンス(Z)とは何か?
まずは「インピーダンス」の正体を理解しましょう。
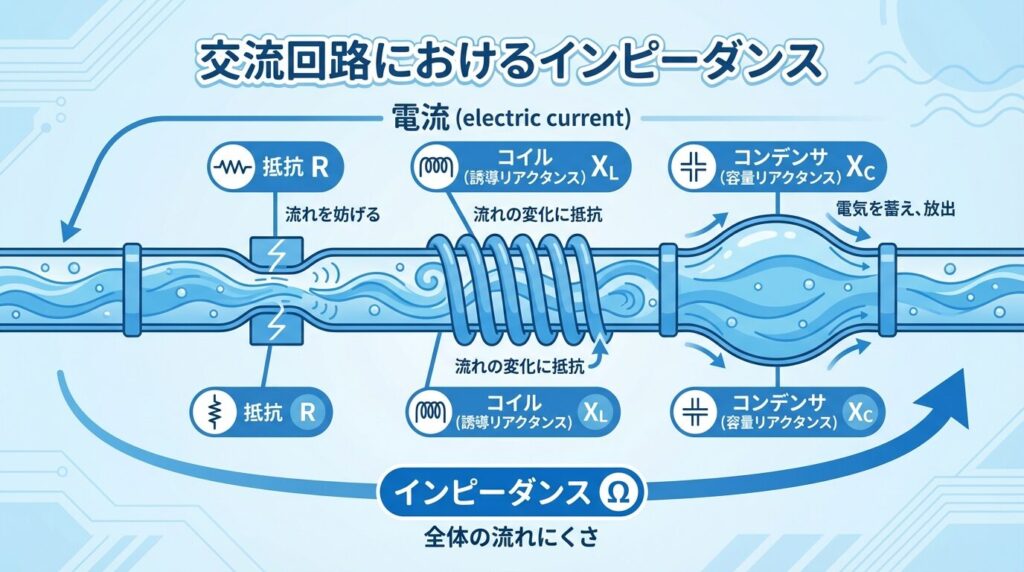
直流と交流の「抵抗」の違い
直流回路では、電流の流れにくさは抵抗Rだけで決まります。
しかし交流回路では、もう2つの要素が加わります。
| 要素 | 記号 | 単位 | 役割 |
|---|---|---|---|
| 抵抗 | R | Ω(オーム) | 電気エネルギーを熱に変換 |
| 誘導性リアクタンス | XL | Ω(オーム) | コイルによる電流の妨げ |
| 容量性リアクタンス | XC | Ω(オーム) | コンデンサによる電流の妨げ |
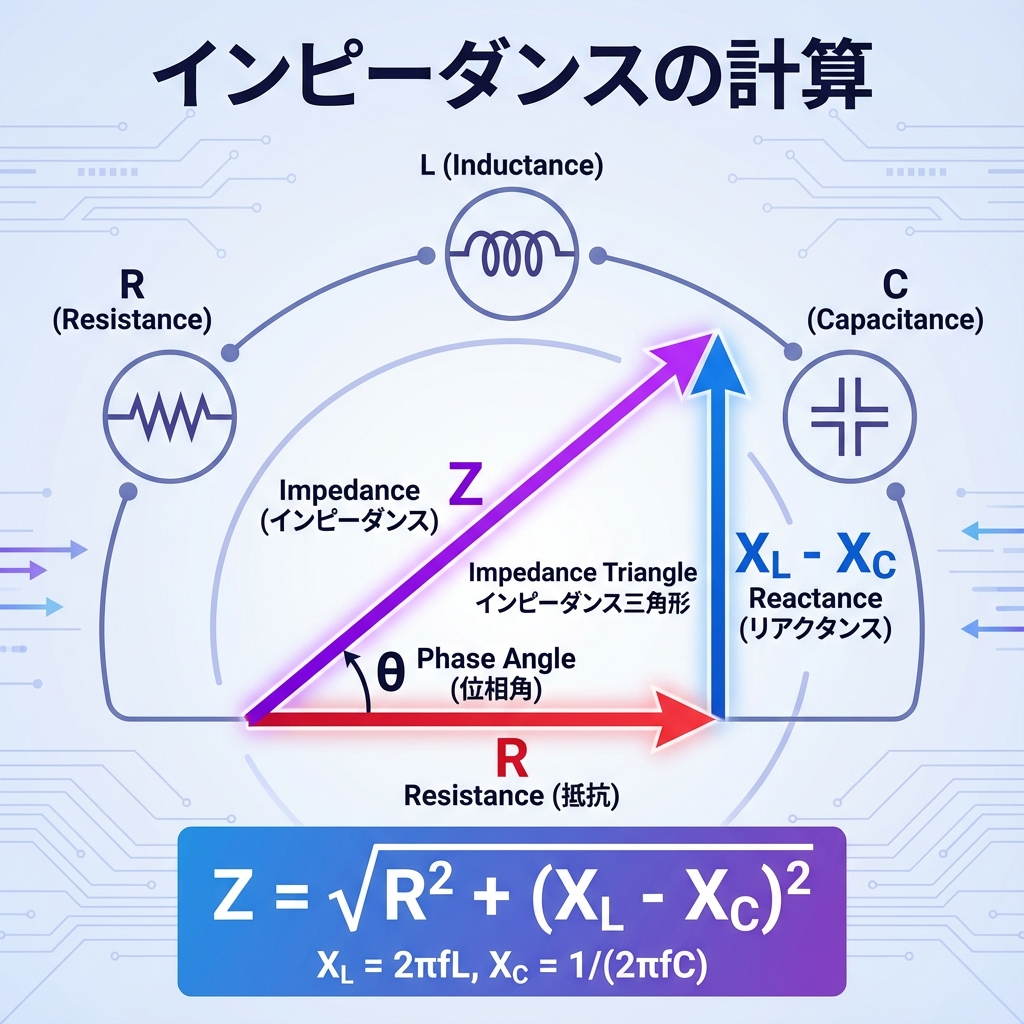
インピーダンス(Z)の定義
交流回路における電流の流れにくさの総合値
R、XL、XCを「ベクトル的に合成」したもの
なぜ単純に足し算できないの?
☕ たとえ話:綱引きのイメージ
3人が綱引きをしていると想像してください。Rさんは横方向に引っ張り、XLさんは上方向に、XCさんは下方向に引っ張っています。全員の力の「合計」を求めるには、単純に足すのではなく、ベクトル(矢印)として合成する必要がありますよね。
これが、インピーダンスの計算で三平方の定理を使う理由です!

🔌 R-L-C直列回路の構成
ここからは、R(抵抗)・L(コイル)・C(コンデンサ)が直列につながった回路を見ていきます。
回路のイメージ
R-L-C直列回路は、交流電源に対して3つの部品が一列につながっている状態です。
🔗 直列回路の特徴
- すべての部品に同じ電流 I が流れる
- 各部品の電圧はそれぞれ異なる(VR、VL、VC)
- 電源電圧は各電圧のベクトル和
各部品のリアクタンス公式
コイルとコンデンサのリアクタンス(交流での抵抗のようなもの)は、周波数によって変わります。
| 部品 | リアクタンス | 特徴 |
|---|---|---|
| コイル(L) | XL = ωL = 2πfL | 周波数が高いほど大きくなる |
| コンデンサ(C) | XC = 1/(ωC) = 1/(2πfC) | 周波数が高いほど小さくなる |
🎯 覚え方
- コイル:「L」は上にある → 周波数と比例(分子に L)
- コンデンサ:「C」は下にある → 周波数と反比例(分母に C)

📐 ベクトル図でインピーダンスを理解する
ここが最重要ポイントです!
R、XL、XCは向きが違うので、ベクトル(矢印)として考える必要があります。
各要素の「向き」
| 要素 | ベクトルの向き | 理由(電流との位相関係) |
|---|---|---|
| 抵抗 R | → 横向き(基準) | 電圧と電流が同位相 |
| XL(コイル) | ↑ 上向き(+90°) | 電圧が電流より90°進む |
| XC(コンデンサ) | ↓ 下向き(−90°) | 電圧が電流より90°遅れる |
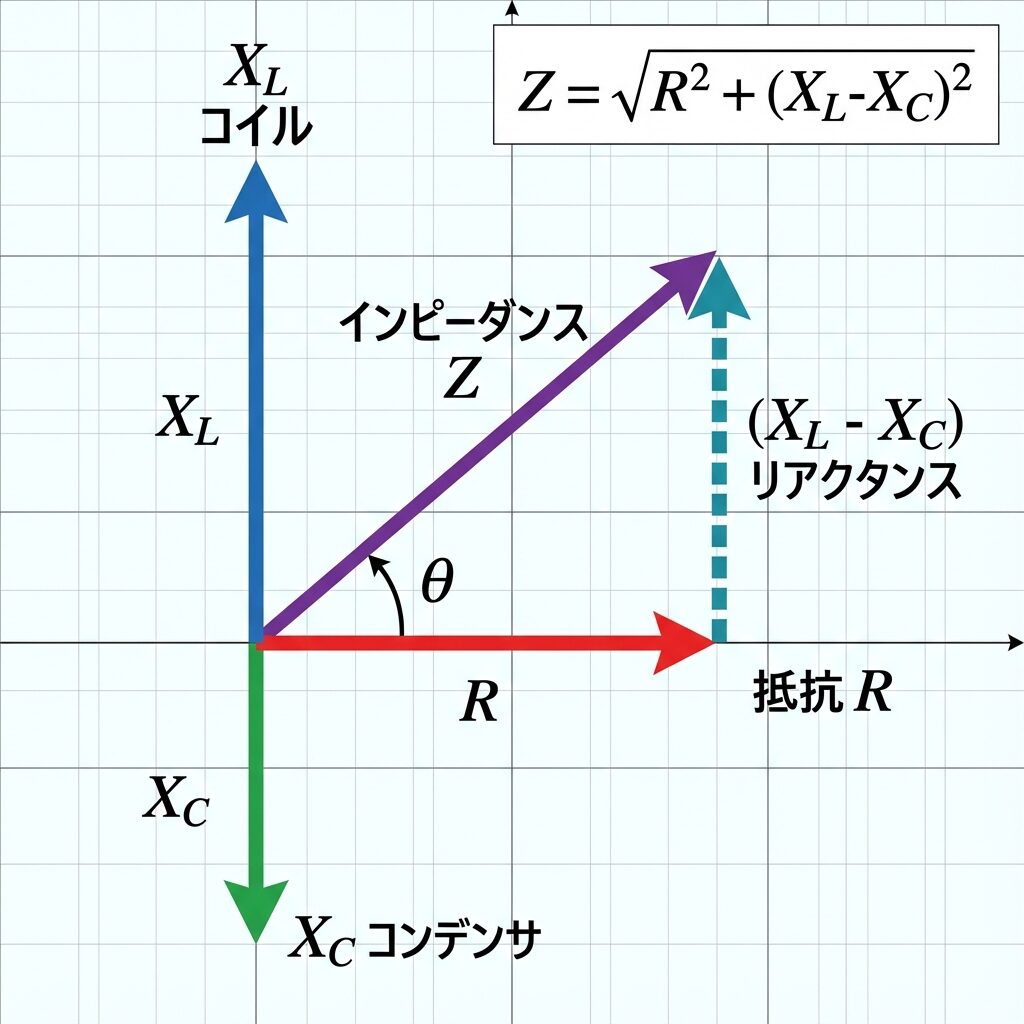
ベクトル図を描いてみよう
これをベクトル図で表すと、次のようになります:
📝 ベクトル図の描き方
- Rを横軸(右向き)に描く
- XLを縦軸(上向き)に描く
- XCを縦軸(下向き)に描く
- XLとXCは逆向きなので引き算になる → XL − XC
- RとXL − XCを三平方の定理で合成 → Z
💡 XL − XC になる理由
XL(上向き)とXC(下向き)は真逆の方向を向いている。
だから、合成すると打ち消し合って引き算になる!
📝 インピーダンスの公式を導出する
ベクトル図を見れば、公式の意味が自然と分かります!
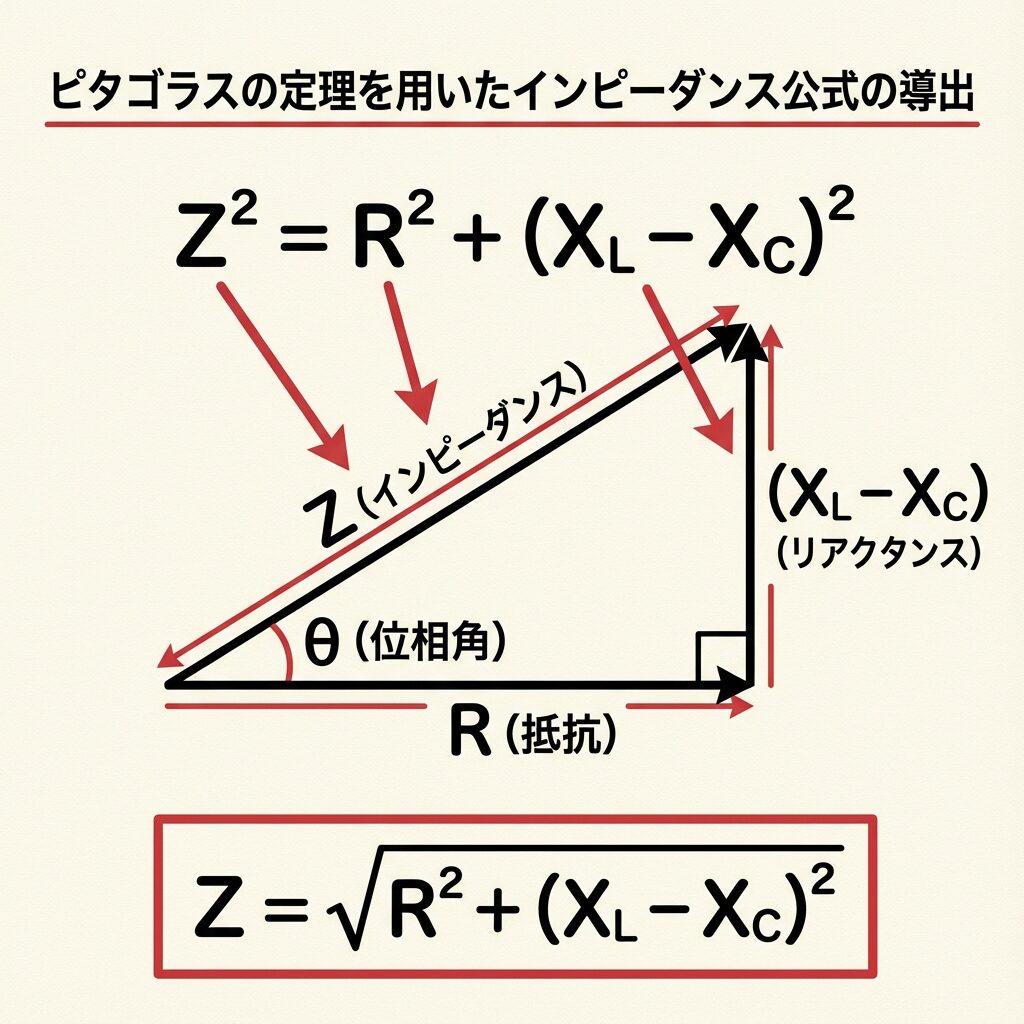
三平方の定理を使う
ベクトル図を見ると、直角三角形ができていますね。
📐 公式の導出
直角三角形の辺の関係より:
Z² = R² + (XL − XC)²
両辺のルートを取ると:
Z = √( R² + (XL − XC)² )
これがR-L-C直列回路のインピーダンス公式です!
🎯 R-L-C直列回路のインピーダンス
Z = √( R² + (XL − XC)² )
単位はすべて Ω(オーム)
位相角θも求められる
インピーダンス三角形から、電圧と電流の位相差(θ)も求められます。
位相角 θ の公式
tan θ = (XL − XC) / R
θ > 0 なら誘導性(遅れ)、θ < 0 なら容量性(進み)
🧮 計算例で確認しよう
公式を使って、実際に計算してみましょう!
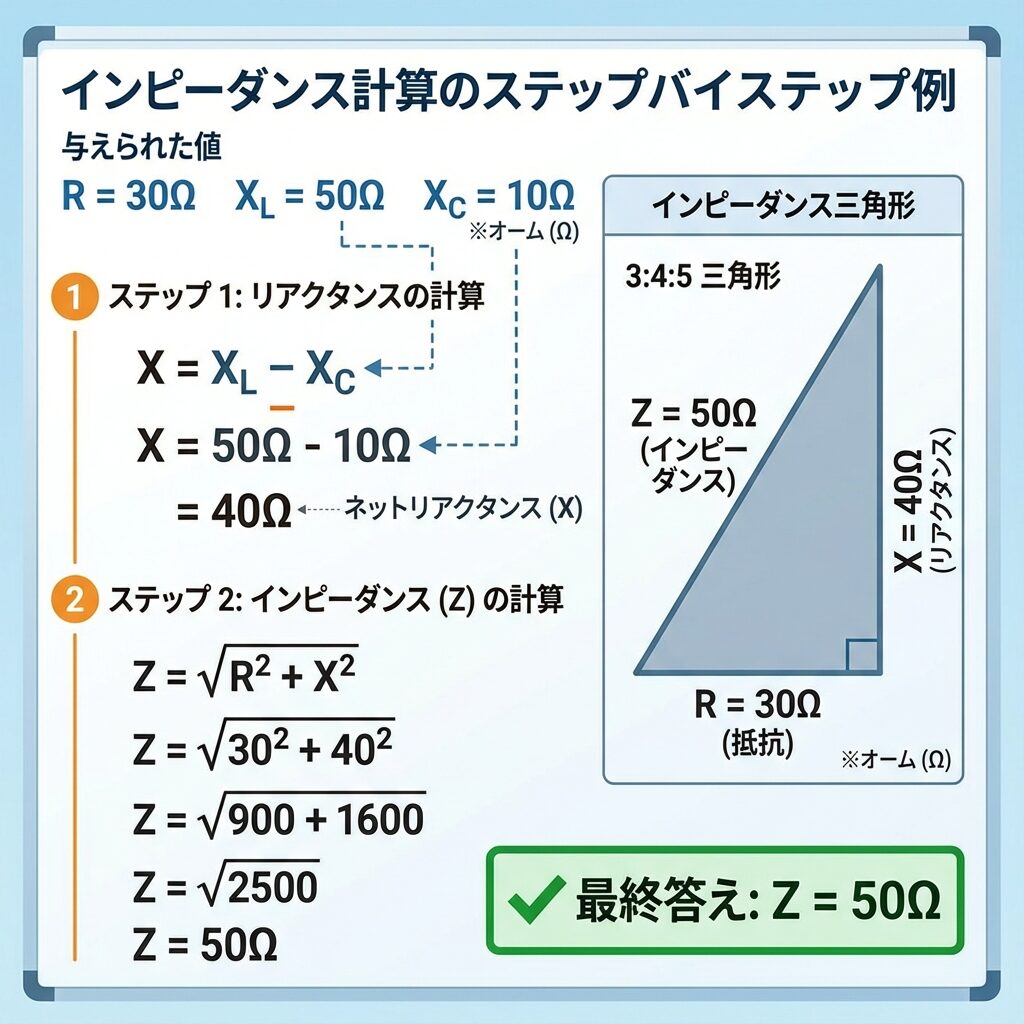
例題1:基本的な計算
📝 問題
R = 30Ω、XL = 50Ω、XC = 10Ω の直列回路がある。インピーダンス Z を求めよ。
✏️ 解答
① まず XL − XC を計算:
XL − XC = 50 − 10 = 40Ω
② 公式に代入:
Z = √(30² + 40²) = √(900 + 1600) = √2500 = 50Ω
∴ Z = 50Ω
💡 ヒント:30² + 40² = 50² は「3:4:5」の三角形!電験ではこの比率がよく出ます。
例題2:電流を求める
📝 問題
上の回路に V = 100V の交流電圧を加えたとき、流れる電流 I を求めよ。
✏️ 解答
オームの法則の交流版を使う:
I = V / Z = 100 / 50 = 2A
∴ I = 2A
例題3:位相角を求める
📝 問題
例題1の回路の位相角 θ を求めよ。
✏️ 解答
位相角の公式を使う:
tan θ = (XL − XC) / R = 40 / 30 = 4/3
θ = arctan(4/3) ≒ 53.1°(遅れ)
∴ θ ≒ 53.1°(電流は電圧より遅れる)
🔍 特殊なケースを押さえよう
R-L-C回路には、いくつかの特殊なパターンがあります。試験でよく出るので押さえておきましょう!
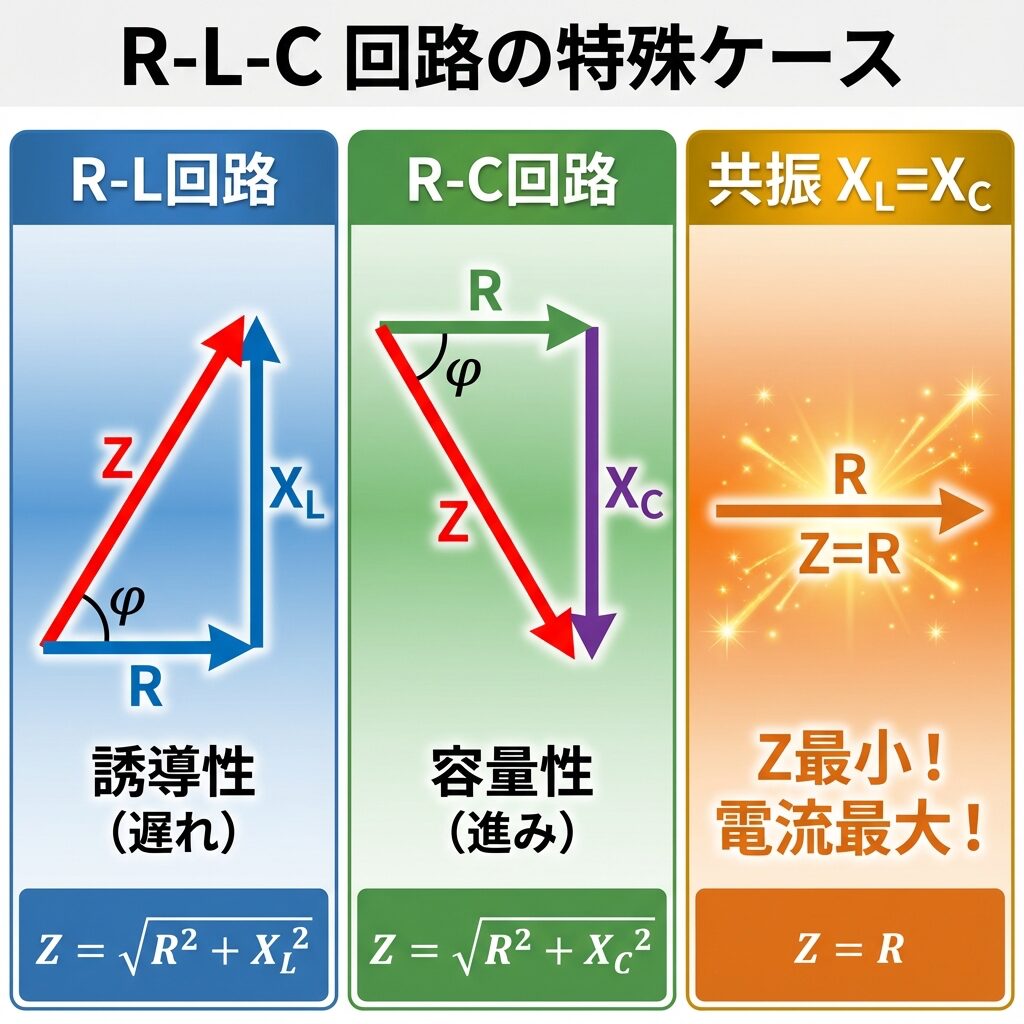
ケース1:R-L回路(コンデンサなし)
XC = 0 の場合
Z = √( R² + XL² )
位相角 θ > 0(電流は電圧より遅れる)→ 誘導性回路
ケース2:R-C回路(コイルなし)
XL = 0 の場合
Z = √( R² + XC² )
位相角 θ < 0(電流は電圧より進む)→ 容量性回路
ケース3:共振状態(XL = XC)
⚡ 直列共振(超重要!)
XL = XC のとき:
Z = √( R² + 0² ) = R
- インピーダンスが最小になる(= Rだけ)
- 電流が最大になる
- 位相角 θ = 0°(電圧と電流が同位相)
共振周波数 f₀ の公式
f₀ = 1 / (2π√(LC))
📌 まとめ
この記事のポイント
- インピーダンス(Z)は交流回路における電流の流れにくさの総合値
- R、XL、XCは向きが違うので単純に足せない
- XLは上向き、XCは下向き → 引き算になる
- 公式:Z = √( R² + (XL − XC)² )
- 共振時(XL = XC)は Z = R で最小、電流は最大
📋 公式チートシート
| 誘導性リアクタンス | XL = ωL = 2πfL |
| 容量性リアクタンス | XC = 1/(ωC) = 1/(2πfC) |
| インピーダンス | Z = √( R² + (XL − XC)² ) |
| 位相角 | tan θ = (XL − XC) / R |
| 共振周波数 | f₀ = 1 / (2π√(LC)) |
インピーダンスの計算は、ベクトル図をイメージできるようになれば怖くありません。
「三平方の定理」と「XLとXCは打ち消し合う」この2点を押さえて、交流回路の問題に自信を持って挑みましょう!
💡 ベクトル図を描く練習をすると、インピーダンスの理解がグッと深まります!