🍪 この記事を読んでいるあなたへ
「np管理図とp管理図、何が違うの?」
「不適合品数と不適合品率、どっちを管理すればいいの?」
「計算式が複雑そうで不安…」
大丈夫です。この記事では、クッキー工場の不良品検査を例に、2つの管理図の違いと計算方法をわかりやすく解説します!
目次
🎯 この記事でわかること
✅ np管理図とp管理図の違い
✅ どちらを使うかの判断基準
✅ それぞれの計算方法と公式
✅ 例題を使った実践的な作り方
✅ QC検定でよく出る問題パターン
📍 シリーズ全体像|今ここ!
管理図シリーズ(全12記事)
① ロードマップ → ② バラつき入門 → ③ 管理図とは → ④ 種類一覧 → ⑤ 異常判定ルール → ⑥ 読み方・活用法 → ⑦ X̄-R管理図 → ⑧ その他計量値
⑨ np管理図・p管理図 ← 今ここ!
→ ⑩ c・u管理図 → ⑪ Cp・Cpk → ⑫ 判定基準
💡 前の記事を読んでいない方へ
管理図の種類と選び方がわからない方は、先にこちらの記事をご覧ください。

🔍 まず結論!np管理図とp管理図の違い
結論から言うと、検査する数が毎回同じかどうかで決まります。
np管理図
不適合品「数」を管理
使う条件:
検査数が毎回同じ
p管理図
不適合品「率」を管理
使う条件:
検査数が毎回変わる
🍪 クッキー工場でたとえると
あなたはクッキー工場の品質管理担当。毎日、焼き上がったクッキーの中から不良品(割れ・焦げ)をチェックしています。
📦 np管理図を使う場合
毎日100枚ぴったり検査
→「今日は3枚不良」「昨日は5枚」
→ 枚数で管理できる!
📊 p管理図を使う場合
月曜80枚、火曜120枚、水曜95枚…
→ 枚数が違うから比較できない
→ 割合(%)で管理!
📋 用語を整理しよう
| 記号 | 読み方 | 意味 |
|---|---|---|
| n | エヌ | サンプルサイズ(検査した数) |
| np | エヌピー | 不適合品数(不良品の数) |
| p | ピー | 不適合品率(不良品の割合) |
| p̄ | ピーバー | 平均不適合品率 |
💡 覚え方のコツ
「nが一定ならnp」「nがバラバラならp」と覚えましょう!
🔀 選び方フローチャート
不適合品「数」で管理
不適合品「率」で管理
📦 np管理図の作り方
STEP1:データを集める
毎日100枚のクッキーを検査して、不良品の数を記録しました。
| 日 | 検査数 n | 不適合品数 np |
|---|---|---|
| 1日目 | 100 | 3 |
| 2日目 | 100 | 5 |
| 3日目 | 100 | 2 |
| 4日目 | 100 | 4 |
| 5日目 | 100 | 6 |
| 合計 | 500 | 20 |
STEP2:平均不適合品率 p̄ を求める
公式
p̄ = 不適合品の合計 ÷ 検査数の合計
計算:
p̄ = 20 ÷ 500 = 0.04(= 4%)
STEP3:管理限界線を計算する
np管理図の公式
CL = n × p̄
UCL = n × p̄ + 3√(n × p̄ × (1 − p̄))
LCL = n × p̄ − 3√(n × p̄ × (1 − p̄))
🔢 √の中身をシンプルに
√(n × p̄ × (1 − p̄)) は「標準偏差」にあたる部分です。
「±3σ」の範囲を求めているんですね!
例題の計算
n = 100、p̄ = 0.04 のとき
① CL(中心線)
CL = 100 × 0.04 = 4.0
② √の中身を計算
n × p̄ × (1 − p̄) = 100 × 0.04 × 0.96 = 3.84
√3.84 = 1.96
③ UCL(上方管理限界)
UCL = 4.0 + 3 × 1.96 = 4.0 + 5.88 = 9.88 ≒ 9.9
④ LCL(下方管理限界)
LCL = 4.0 − 3 × 1.96 = 4.0 − 5.88 = −1.88 → 0
※ マイナスになったら0とする(不良品数はマイナスにならない)
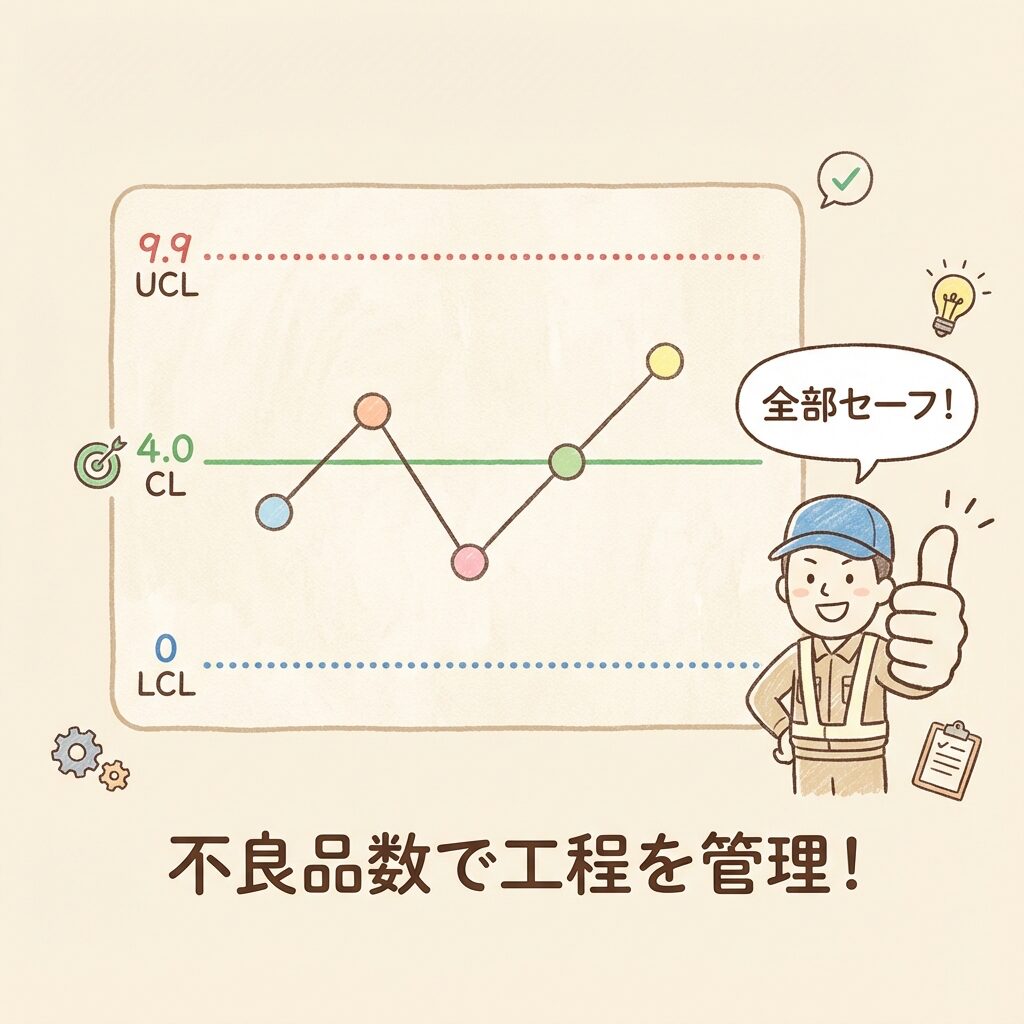
📊 計算結果まとめ
| 管理線 | 値 | 意味 |
|---|---|---|
| UCL | 9.9枚 | これ以上は異常 |
| CL | 4.0枚 | 平均的な不良品数 |
| LCL | 0枚 | 下限なし |
💡 判定の仕方
1日の不良品が10枚以上出たら「異常あり!」と判断します。
すべての日(3, 5, 2, 4, 6枚)が9.9以下なので、この工程は安定しています。
📊 p管理図の作り方
STEP1:データを集める
今度は検査数が日によって違うケースです。
| 日 | 検査数 n | 不適合品数 | 不適合品率 p |
|---|---|---|---|
| 1日目 | 80 | 4 | 4÷80 = 0.050 |
| 2日目 | 120 | 5 | 5÷120 = 0.042 |
| 3日目 | 100 | 3 | 3÷100 = 0.030 |
| 4日目 | 90 | 5 | 5÷90 = 0.056 |
| 5日目 | 110 | 3 | 3÷110 = 0.027 |
| 合計 | 500 | 20 | − |
⚠️ 注目ポイント
検査数(n)が80〜120とバラバラ!
だから「5個不良」と言われても、良いのか悪いのか判断できませんよね。
そこで「割合(p)」に変換して比較するのです。
STEP2:平均不適合品率 p̄ を求める
計算(np管理図と同じ):
p̄ = 20 ÷ 500 = 0.04(= 4%)
STEP3:管理限界線を計算する
p管理図の公式
CL = p̄
UCL = p̄ + 3√(p̄ × (1 − p̄) ÷ n)
LCL = p̄ − 3√(p̄ × (1 − p̄) ÷ n)
🚨 重要!p管理図の特徴
公式に「n」が含まれているので、検査数が変わるとUCL・LCLも変わります!
→ 管理限界線が「ギザギザ」になるのがp管理図の特徴です。
例題の計算(1日目:n=80)
① CL(中心線)
CL = p̄ = 0.04(全日共通)
② √の中身を計算
p̄ × (1 − p̄) ÷ n = 0.04 × 0.96 ÷ 80 = 0.00048
√0.00048 = 0.0219
③ UCL(上方管理限界)
UCL = 0.04 + 3 × 0.0219 = 0.04 + 0.066 = 0.106(10.6%)
④ LCL(下方管理限界)
LCL = 0.04 − 3 × 0.0219 = 0.04 − 0.066 = −0.026 → 0
📊 各日の管理限界線
| 日 | n | UCL | CL | LCL | 実測p | 判定 |
|---|---|---|---|---|---|---|
| 1 | 80 | 0.106 | 0.04 | 0 | 0.050 | ○ |
| 2 | 120 | 0.094 | 0.04 | 0 | 0.042 | ○ |
| 3 | 100 | 0.099 | 0.04 | 0 | 0.030 | ○ |
| 4 | 90 | 0.102 | 0.04 | 0 | 0.056 | ○ |
| 5 | 110 | 0.096 | 0.04 | 0 | 0.027 | ○ |
💡 UCLが変動している理由
nが大きい(120)→ UCLが小さい(0.094)
nが小さい(80)→ UCLが大きい(0.106)
検査数が多いほど「精度が上がる」ので、許容範囲が狭くなるのです!

⚖️ np管理図 vs p管理図 比較まとめ
| 項目 | np管理図 | p管理図 |
|---|---|---|
| 管理するもの | 不適合品数 | 不適合品率 |
| 検査数 n | 一定 | 変動OK |
| 管理限界線 | まっすぐ | ギザギザ |
| 計算の手間 | 楽 | やや手間 |
| CL | n × p̄ | p̄ |
| UCL/LCL | n×p̄ ± 3√(n×p̄×(1−p̄)) | p̄ ± 3√(p̄×(1−p̄)÷n) |
🍪 覚え方のポイント
「n」が一定 → 「n」p管理図(nが付いてる!)
「n」が変動 → 「p」管理図(nが付いてない!)
🎯 QC検定でよく出る問題
パターン①:どちらの管理図を使うか
【問題】
毎日100個のネジを検査し、不良品数を管理したい。適切な管理図は?
【解答】
検査数が毎日100個で一定 → np管理図
【問題】
ロットごとに検査数が異なる。不適合品率を管理したい。適切な管理図は?
【解答】
検査数がロットごとに変動 → p管理図
パターン②:np管理図のCL・UCLを求めよ
【問題】
n = 200、p̄ = 0.05 のとき、np管理図のCLとUCLを求めよ。
【解答】
CL = n × p̄ = 200 × 0.05 = 10
√(n × p̄ × (1−p̄)) = √(200 × 0.05 × 0.95) = √9.5 = 3.08
UCL = 10 + 3 × 3.08 = 10 + 9.24 = 19.24
パターン③:p管理図で異常判定
【問題】
p管理図でUCL = 0.08のとき、ある日のp = 0.09だった。この工程は正常か?
【解答】
0.09 > 0.08(UCL)なので、異常と判定する
🔗 関連記事
異常判定の8つのルールはこちらの記事で詳しく解説しています。

📝 公式まとめ(試験直前チェック用)
📦 np管理図
CL = n × p̄
UCL = n×p̄ + 3√(n×p̄×(1−p̄))
LCL = n×p̄ − 3√(n×p̄×(1−p̄))
※ nが一定のとき使用
📊 p管理図
CL = p̄
UCL = p̄ + 3√(p̄×(1−p̄)÷n)
LCL = p̄ − 3√(p̄×(1−p̄)÷n)
※ nが変動するとき使用
✨ この記事のまとめ
✅ np管理図:検査数が一定 → 不適合品「数」で管理
✅ p管理図:検査数が変動 → 不適合品「率」で管理
✅ 共通点:p̄(平均不適合品率)を先に求める
✅ 違い:p管理図はUCL・LCLがギザギザになる
✅ LCL:マイナスになったら0とする
🗺️ シリーズ記事一覧
① 全体像
管理図と工程能力指数の完全ロードマップ② 超入門
品質管理の"バラつき"って何?③ 基礎
管理図とは?UCL・CL・LCLの意味④ 種類
管理図の種類一覧と選び方⑤ 判定
管理図の異常判定ルール8つ⑥ 活用
管理図の読み方|異常を見つけたら?⑦ 計量値①
X̄-R管理図の作り方⑧ 計量値②
X-Rs・Me-R・X̄-s管理図の計算方法⑨ 今ここ!
np管理図・p管理図の作り方
⑩ 計数値②
c管理図・u管理図の作り方⑪ 工程能力①
工程能力指数Cp・Cpkとは?⑫ 工程能力②
工程能力指数の判定基準🎉 お疲れ様でした!
「不適合品」の管理図をマスターしました!
次は「不適合数」を管理するc・u管理図に進みましょう。