A2・D3・D4とは何ですか？

X̄-R管理図の管理限界線を R̄ から計算する係数です。A2 は X̄ 管理図、D4・D3 は R 管理図の上限・下限に使います。

n＝5のときの係数の値は？

A2＝0.577、D4＝2.115（表によっては2.114）、D3 は「－」です。D3 が「－」なので、R 管理図の下限は設けません。

D3に値が出るのはnがいくつから？

n＝7 からです。n＝7 で D3＝0.076、n＝10 で 0.223 となり、R 管理図にも下限の管理限界線が引けるようになります。

管理図の係数表 A2・D3・D4の一覧と使い方｜n＝2〜10の早見表と計算例

※本記事にはプロモーション（広告）が含まれています。

結論：係数は「3σの管理限界線」を簡単に計算するための道具

いきなり結論からお伝えします。A2・D3・D4は、管理限界線（UCL・LCL）を手計算で求めるための「便利な変換係数」です。

本来、管理限界線は「平均±3σ」で計算します。しかし、工程のσ（標準偏差）を直接求めるのは大変です。そこで、範囲R（最大値−最小値）から間接的にσを推定し、さらに計算を簡略化するために係数が用意されているのです。

係数表とは？まず全体像を見てみよう

X̄-R管理図を作るとき、必ず登場するのがこの係数表です。サンプルサイズ（n）ごとに、使う係数の値が決まっています。

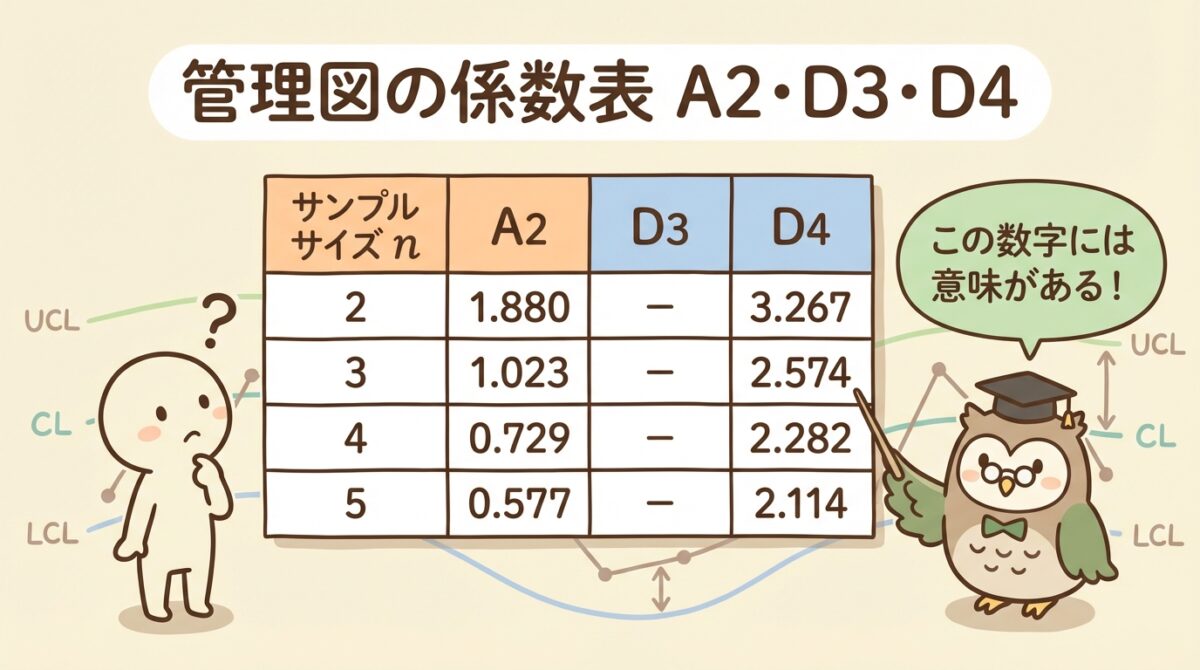
n（サンプルサイズ）	A2	D3	D4
2	1.880	－	3.267
3	1.023	－	2.575
4	0.729	－	2.282
5	0.577	－	2.115
6	0.483	－	2.004
7	0.419	0.076	1.924

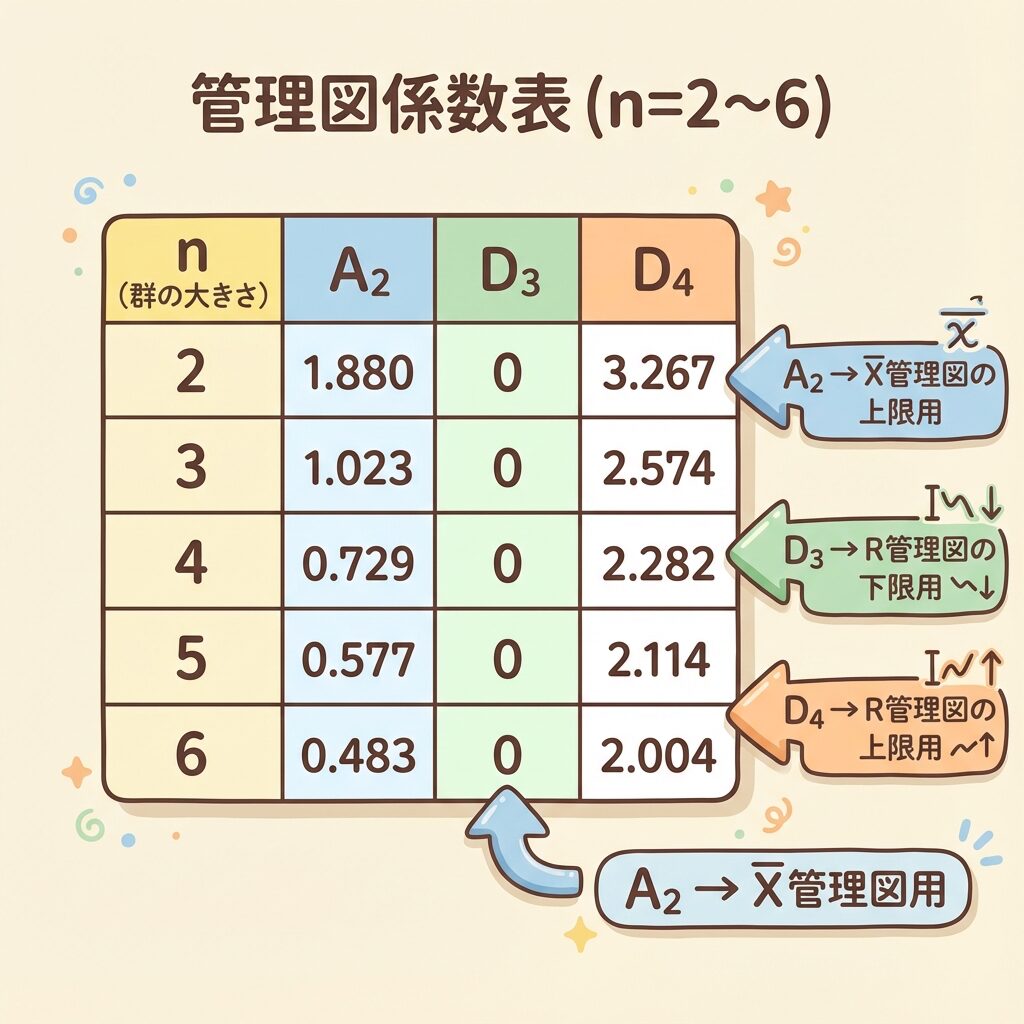
A2・D3・D4、それぞれの役割を理解する

係数が3つあるのは、それぞれ使う場所が違うからです。X̄管理図用とR管理図用で分かれています。

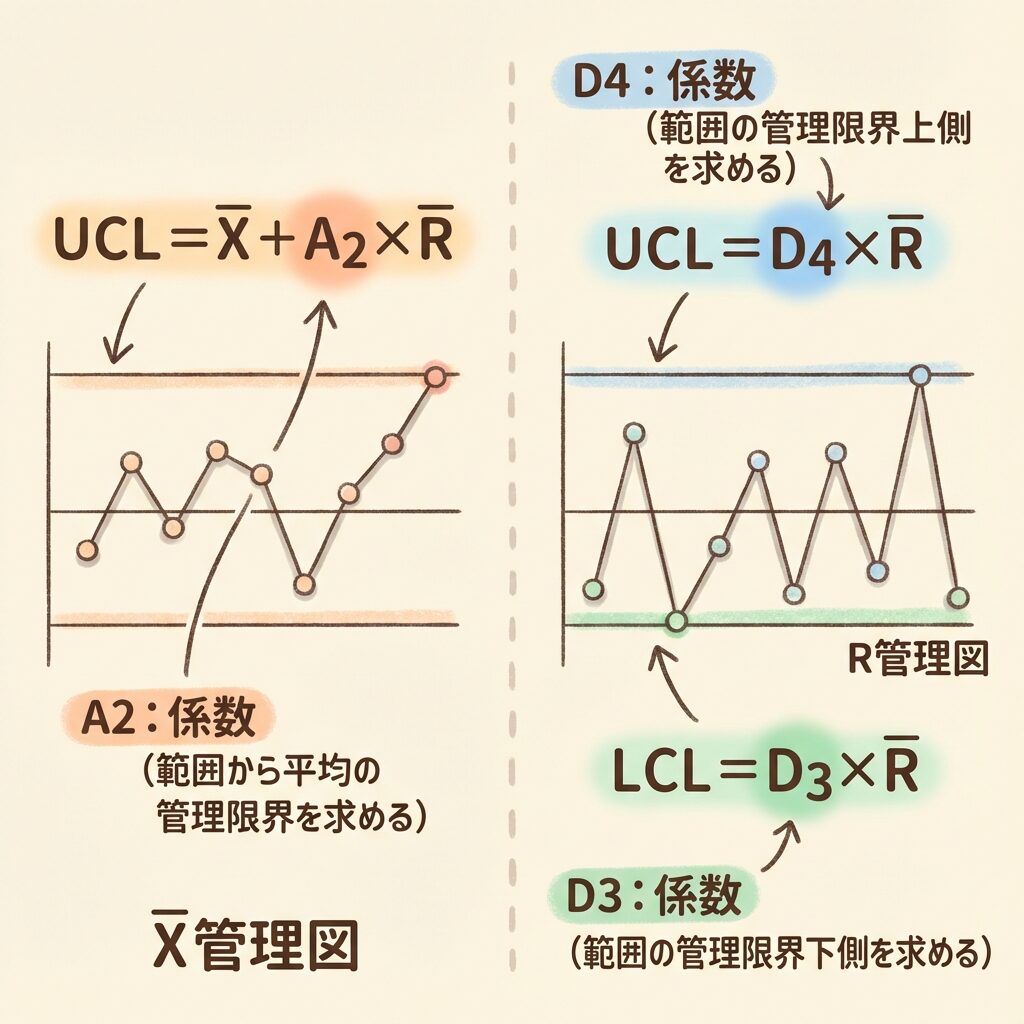
A2：X̄管理図の管理限界に使う

A2は、X̄（平均値）管理図のUCLとLCLを計算するときに使います。

A2は「R̄（範囲の平均）から、X̄のバラつき幅を計算するための変換係数」です。本来は「3σ÷√n」のような計算が必要ですが、A2を使えば「A2×R̄」の1回の掛け算で済みます。

この続きと一緒に読まれている記事

D3・D4：R管理図の管理限界に使う

D3とD4は、R（範囲）管理図のLCLとUCLを計算するときに使います。

D4は上限係数、D3は下限係数です。R̄に掛けるだけで、範囲のバラつきの管理限界が求まります。

係数	使う管理図	計算する線	公式
A2	X̄管理図	UCL・LCL	X̿ ± A2×R̄
D4	R管理図	UCL（上限）	D4×R̄
D3	R管理図	LCL（下限）	D3×R̄

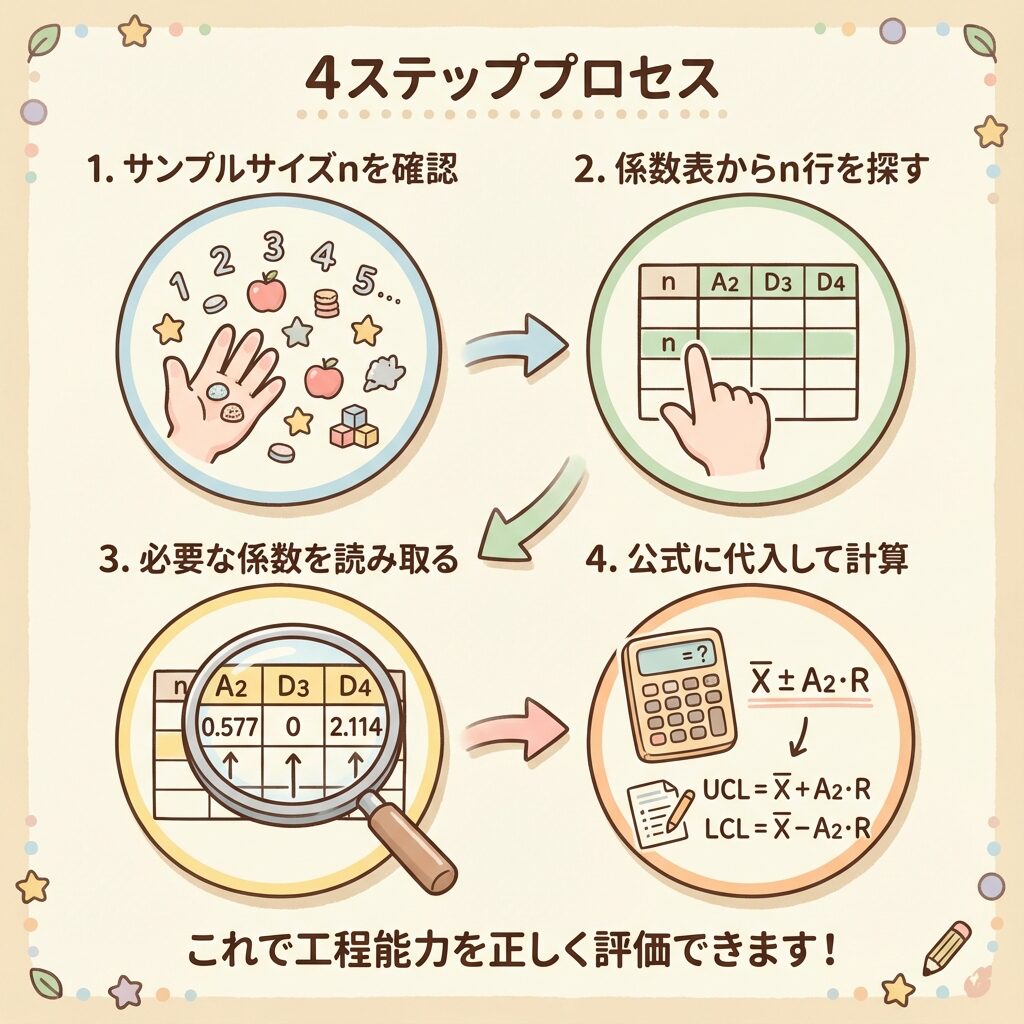
係数表の読み方：4ステップで迷わない

係数表の使い方は、実はとてもシンプルです。以下の4ステップで進めれば、絶対に間違えません。

Step 1：サンプルサイズ（n）を確認する

まず、1つの群（サブグループ）に含まれるデータの個数を確認します。これが「n」です。

例えば「毎日5個サンプリングして測定」なら、n=5です。「1時間に3個抜き取り」ならn=3です。

Step 2：係数表からnの行を探す

係数表の左端にnの値が並んでいます。自分のnに該当する行を見つけましょう。

Step 3：必要な係数を読み取る

X̄管理図を作るならA2を、R管理図を作るならD3とD4を読み取ります。

Step 4：公式に代入して計算する

読み取った係数を、管理限界線の公式に代入します。

よくある間違いと注意点

係数表を使うときに、やりがちな間違いをまとめました。試験前にチェックしておきましょう。

間違い①：nの値を取り違える

最も多い間違いです。「群の数」と「群内のサンプル数」を混同してしまうパターンです。

間違い②：係数を入れ替えてしまう

D3とD4を逆に使ったり、A2をR管理図に使ってしまったりする間違いです。

間違い③：D3が「－」のときの処理

n≦6のとき、D3は「－」です。このとき、「0を代入する」のか「LCLを設けない」のか、問題文の指示を確認しましょう。

なぜこの係数になるのか？（発展）

「A2=0.577って、どこから出てきた数字？」と疑問に思った方もいるでしょう。実は、これらの係数には統計学的な導出過程があります。

簡単に言うと、「範囲Rから標準偏差σを推定し、さらに3σの管理限界を計算する」という複数のステップを、1つの係数にまとめたものです。

この導出原理を理解すると、係数の意味がより深くわかります。興味がある方は、以下の記事で詳しく解説しています。

係数表の続き（n＝8〜10）と、X－Rs管理図の係数

上の表は n＝7 までです。1群のサンプル数が多いときに使う n＝8〜10 の値を足します。n が大きくなると D3 に値が出て、R 管理図にも下限の線が引けるようになります。

n	A2	D3	D4
8	0.373	0.136	1.864
9	0.337	0.184	1.816
10	0.308	0.223	1.777

計算例：n＝8 のとき（X̿＝50.0、R̄＝4.0）

n＝5 の例と比べると、X̄管理図の幅が狭くなっています。1群のデータが多いほど平均値のばらつきが小さくなるので、管理限界線の幅も狭くなります。

1個ずつ測るとき（X－Rs管理図）の係数

1群に1個しかデータがない X－Rs 管理図では、となり合う2個の差（移動範囲 Rs）を使い、n＝2 の係数を使います。

管理図	UCL・LCL	使う係数
X管理図（個々の値）	X̄ ± 2.659×R̄s	E2＝2.659
Rs管理図（移動範囲）	UCL＝3.267×R̄s（LCL は設けない）	D4＝3.267（n＝2）

よくある質問

まとめ：係数表は「便利なショートカット」

係数表は、一見すると「謎の数字の羅列」に見えます。しかし、その正体は「複雑な計算を省略するための便利ツール」です。

使い方さえ覚えてしまえば、あとは表を引いて公式に代入するだけ。X̄-R管理図の計算が、グッと楽になります。

「なぜこの係数になるのか」をもっと深く知りたい方は、関連記事で導出原理を解説していますので、ぜひ読んでみてください。