- 管理図の公式が多すぎて覚えられない…
- UCL・LCLの計算問題で、どの公式を使えばいいか分からない
- A₂やD₄などの係数表の使い方がイマイチ理解できない
- QC検定の過去問で管理図の計算問題が出ると手が止まる
- 全8種類の管理図のUCL・CL・LCL公式を一覧表で総整理
- 計量値・計数値それぞれの公式の「覚え方」と「使い分け」
- 係数表(A₂・D₃・D₄)の意味と使い方
- QC検定頻出の計算パターンを例題で完全マスター
管理図の計算問題は、QC検定2級・3級でほぼ毎回出題される超頻出分野です。
でも、X̄-R管理図、p管理図、c管理図…と種類が多く、それぞれ公式が違うので「どれがどれだっけ?」と混乱しますよね。
この記事では、全管理図の公式を「チートシート」として1ページにまとめました。試験直前の確認や、実務での参照用としてブックマークしておくと便利です。
まずは「公式一覧表」で全体像をつかみ、その後で各管理図の詳細を確認していきましょう。
目次
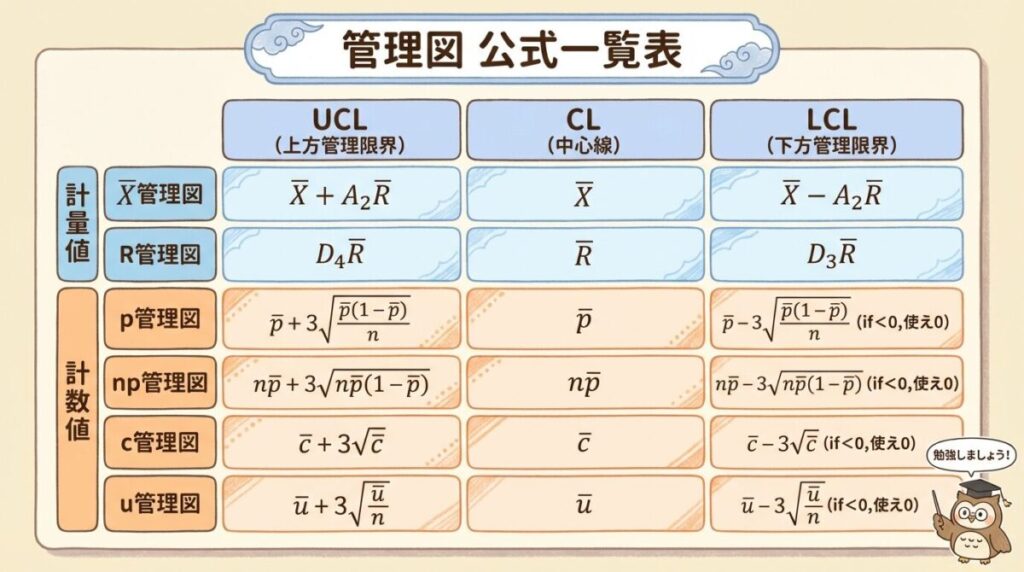
【保存版】管理図の公式一覧表(チートシート)
まずは結論から。全8種類の管理図のUCL・CL・LCL公式を一覧表にまとめました。
この表を見れば、「どの管理図で、どの公式を使うか」が一目でわかります。
計量値の管理図(X̄-R系・X̄-s系)
計量値とは、長さ・重さ・時間など「測定できるデータ」のこと。連続的な数値データを扱います。
| 管理図 | UCL(上方管理限界) | CL(中心線) | LCL(下方管理限界) | 用途 |
|---|---|---|---|---|
| X̄管理図 | X̿ + A₂R̄ | X̿ | X̿ − A₂R̄ | 平均値の管理 |
| R管理図 | D₄R̄ | R̄ | D₃R̄ | 範囲の管理 |
| X管理図 | X̄ + 2.66Rs̄ | X̄ | X̄ − 2.66Rs̄ | 個々の値 |
| Rs管理図 | 3.27Rs̄ | Rs̄ | 0 | 移動範囲 |
計数値の管理図(p・np・c・u)
計数値とは、不良品の個数や欠点の数など「数えるデータ」のこと。離散的な数値データを扱います。
| 管理図 | UCL(上方管理限界) | CL | LCL(下方管理限界) | 用途 |
|---|---|---|---|---|
| p管理図 | p̄ + 3√{p̄(1−p̄)/n} | p̄ | p̄ − 3√{p̄(1−p̄)/n} | 不適合品率 |
| np管理図 | np̄ + 3√{np̄(1−p̄)} | np̄ | np̄ − 3√{np̄(1−p̄)} | 不適合品数 |
| c管理図 | c̄ + 3√c̄ | c̄ | c̄ − 3√c̄ | 不適合数(一定面積) |
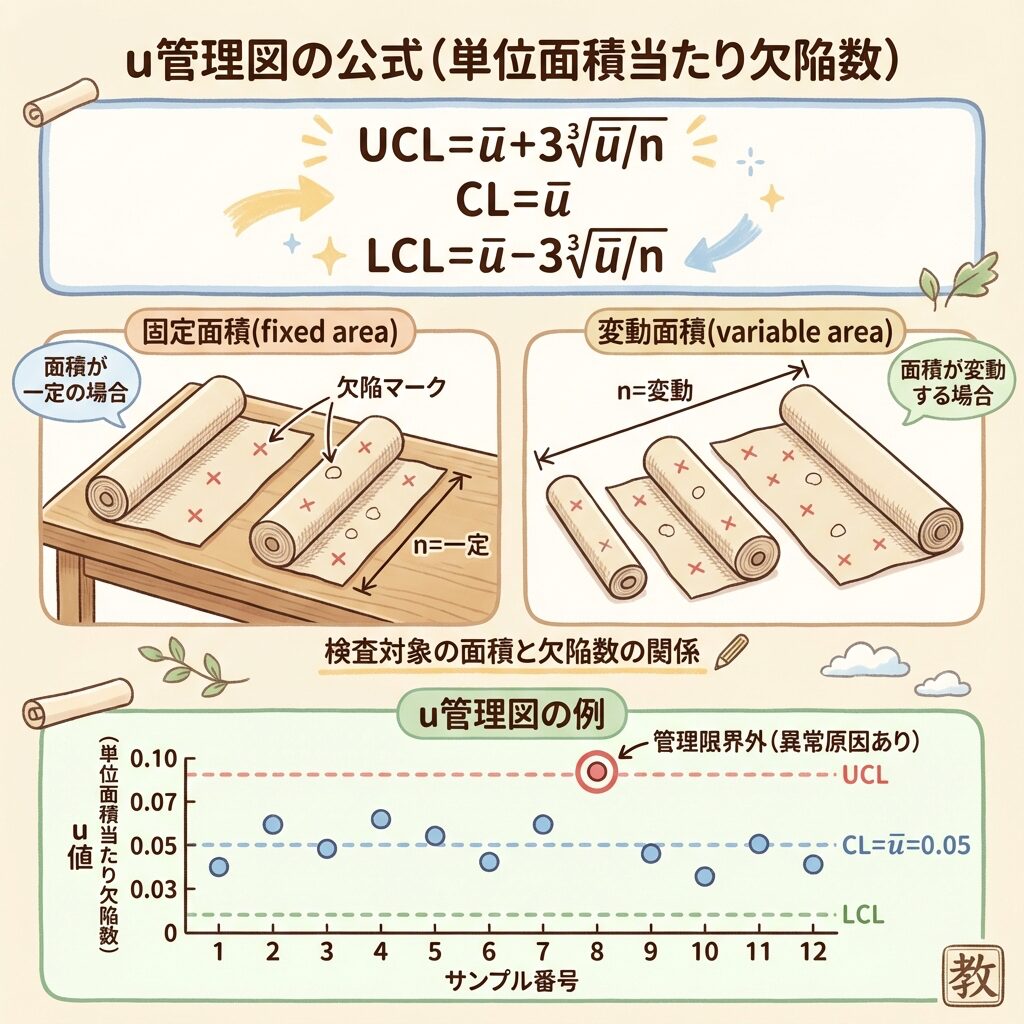
| u管理図 | ū + 3√(ū/n) | ū | ū − 3√(ū/n) | 不適合数(面積変動) |
- 計量値:係数(A₂、D₃、D₄)を使う → 係数表が必要
- 計数値:3σの公式(±3√〜)を使う → ルート計算が必要
- LCLが負になったら「0」とする(不良率や欠点数はマイナスにならない)
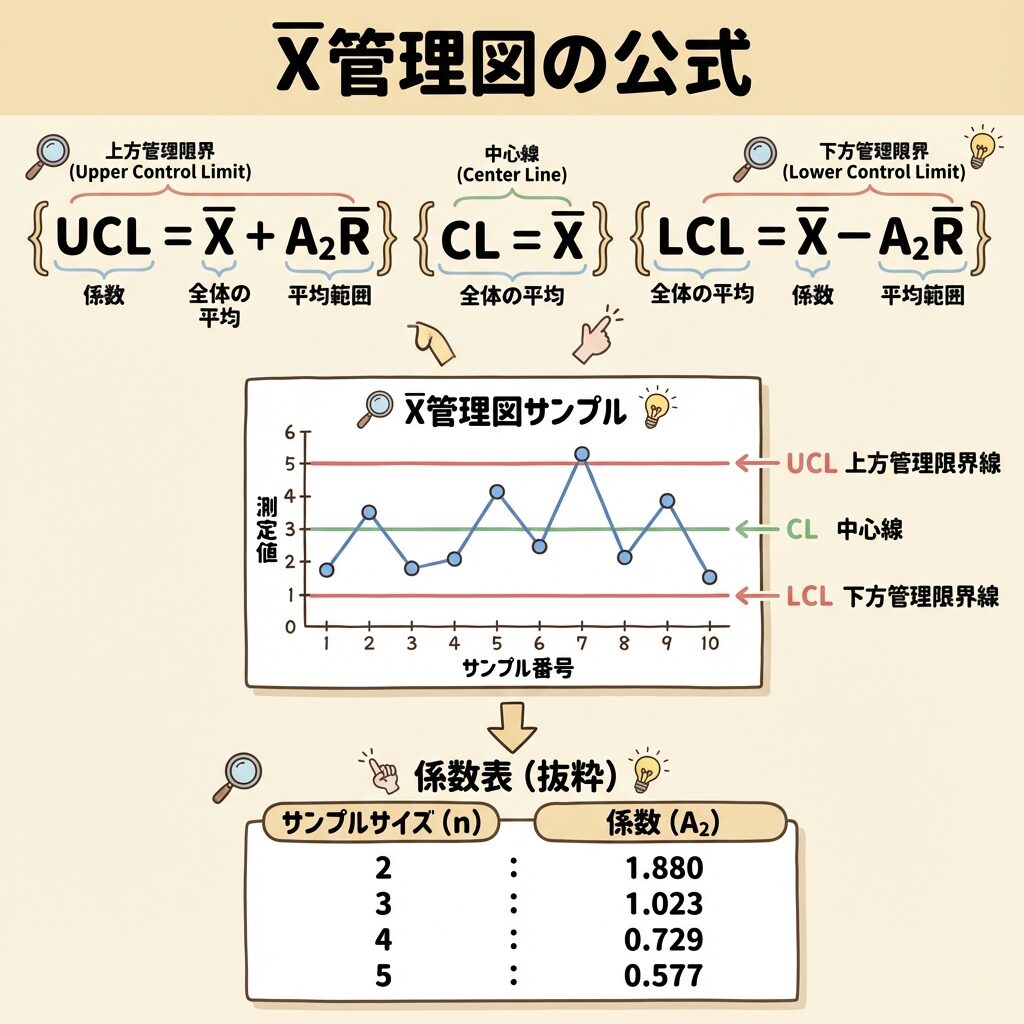
【計量値①】X̄管理図のUCL・LCLの求め方
X̄(エックスバー)管理図は、サンプルの「平均値」を管理するための図です。QC検定で最も出題頻度が高い管理図なので、確実にマスターしましょう。
X̄管理図の公式
記号の意味
| 記号 | 読み方 | 意味 |
|---|---|---|
| X̿ | エックスダブルバー | 全サンプル平均値の平均(総平均) |
| R̄ | アールバー | 範囲(最大−最小)の平均 |
| A₂ | エーツー | 係数(サンプルサイズnで決まる) |
【例題】X̄管理図のUCL・LCLを求める
ある工程で、サンプルサイズn=5で25群のデータを取った結果、以下の値が得られた。X̄管理図のUCL、CL、LCLを求めよ。
- 総平均 X̿ = 50.0
- 範囲の平均 R̄ = 4.0
- 係数 A₂ = 0.577(n=5のとき)
解答
Step 1:CLを求める
CL = X̿ = 50.0
Step 2:UCLを求める
UCL = X̿ + A₂R̄
= 50.0 + 0.577 × 4.0
= 50.0 + 2.308 = 52.308
Step 3:LCLを求める
LCL = X̿ − A₂R̄
= 50.0 − 0.577 × 4.0
= 50.0 − 2.308 = 47.692
X̄管理図では、A₂R̄の部分を先に計算しておくと、UCLとLCLの計算がラクになります。「X̿ ± A₂R̄」と覚えましょう。
【QC検定】X̄-R管理図の作り方|計算方法を例題で完全理解 →
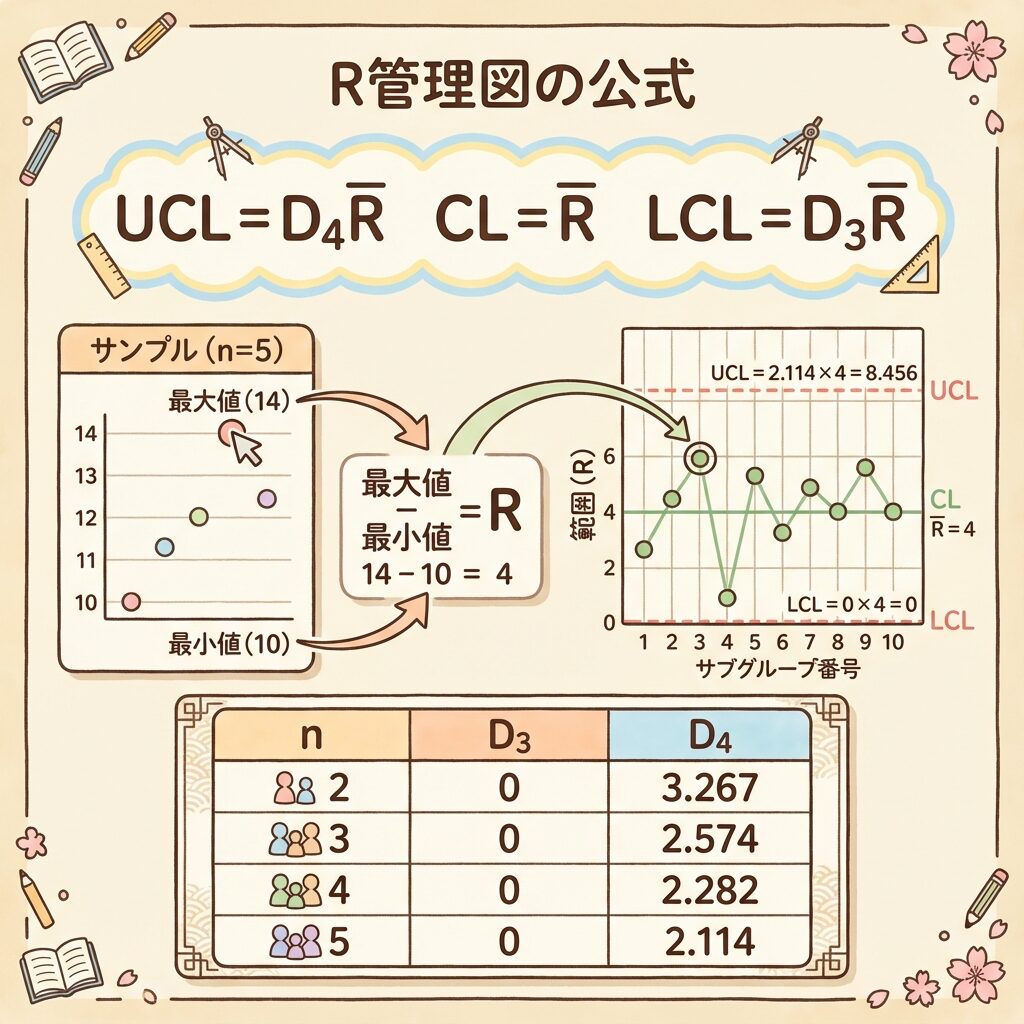
【計量値②】R管理図のUCL・LCLの求め方
R管理図は、サンプルの「範囲(バラつき)」を管理するための図です。X̄管理図とセットで使い、「平均値」と「バラつき」の両方を監視します。
R管理図の公式
係数D₃・D₄の値(よく使う範囲)
| n(サンプルサイズ) | D₃ | D₄ |
|---|---|---|
| 2 | − | 3.267 |
| 3 | − | 2.575 |
| 4 | − | 2.282 |
| 5 | − | 2.115 |
| 6 | − | 2.004 |
| 7 | 0.076 | 1.924 |
n≦6のときはD₃が「−」(存在しない)ため、LCLは計算しません(LCLなし、または0とする)。これはR管理図特有の性質で、試験でもよく問われます。
【例題】R管理図のUCL・LCLを求める
先ほどと同じデータ(n=5、R̄=4.0)を使って、R管理図のUCL、CL、LCLを求めよ。
解答
n=5なので、係数表より D₃=−(なし)、D₄=2.115
UCL = D₄R̄ = 2.115 × 4.0 = 8.46
CL = R̄ = 4.0
LCL = D₃R̄ = なし(または0)
【QC検定】管理図の係数表A₂・D₃・D₄とは?意味と使い方を完全解説 →
【計量値③】X-Rs管理図(個々のデータ用)
X-Rs管理図は、サンプルサイズn=1(1個ずつ測定)の場合に使う管理図です。化学プラントなど、連続的に1点ずつデータを取る工程で使われます。
X-Rs管理図の公式
記号の意味
| 記号 | 読み方 | 意味 |
|---|---|---|
| X̄ | エックスバー | 個々のデータの平均値 |
| Rs̄ | アールエスバー | 移動範囲(隣り合うデータの差)の平均 |
| 2.66 | − | X管理図用の係数(= 3/d₂、n=2のとき) |
| 3.27 | − | Rs管理図用の係数(= D₄、n=2のとき) |
移動範囲とは、隣り合う2つのデータの差の絶対値のこと。
例:データが 10, 12, 9, 11 の場合
Rs₁ = |12−10| = 2
Rs₂ = |9−12| = 3
Rs₃ = |11−9| = 2
Rs̄ = (2+3+2)/3 = 2.33
【計数値①】p管理図のUCL・LCLの求め方
ここからは計数値の管理図です。計数値とは「不良品の個数」や「欠点の数」など、数えて得られるデータのこと。
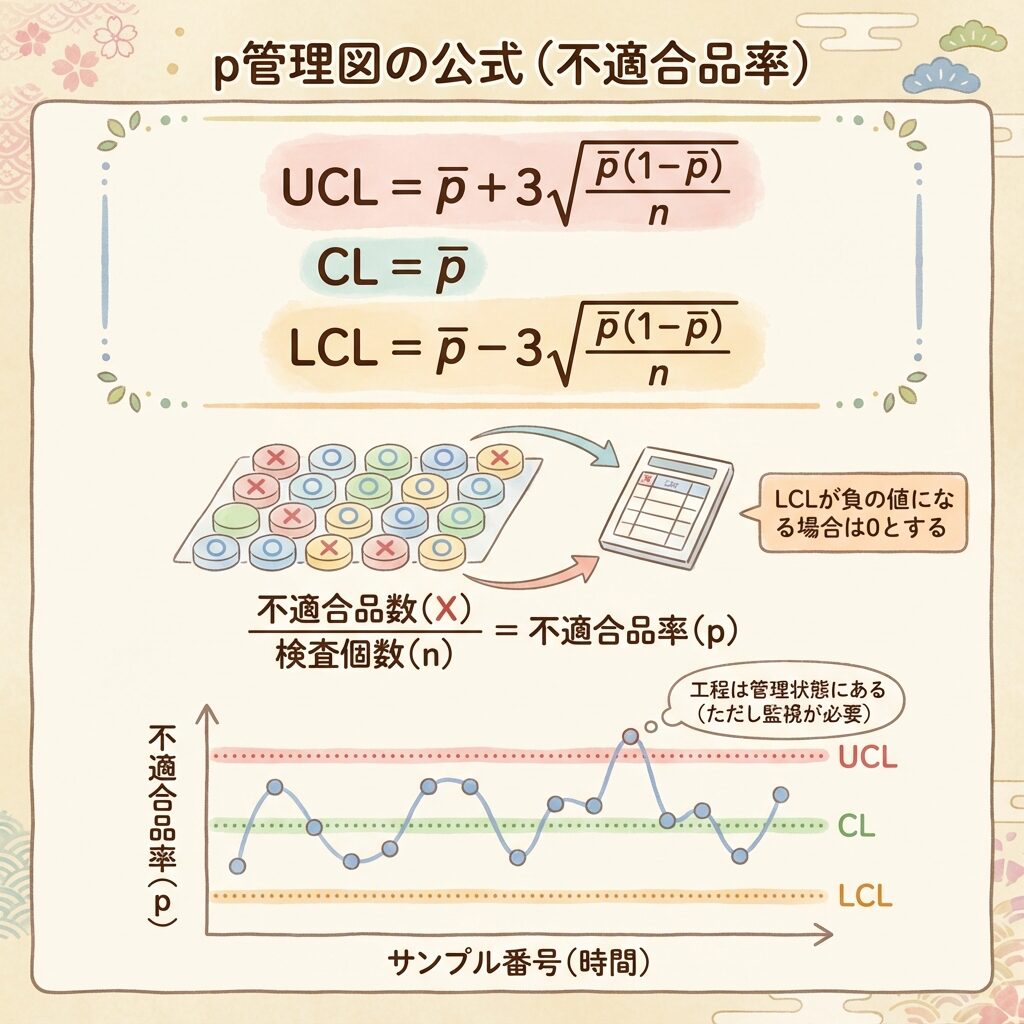
p管理図は、不適合品率(不良率)を管理するための図です。「100個検査して3個不良 → 不良率3%」のように、率(割合)で管理します。
p管理図の公式
※ LCLが負になる場合は LCL = 0 とする
記号の意味
| 記号 | 読み方 | 意味 |
|---|---|---|
| p̄ | ピーバー | 平均不適合品率(= 総不適合品数 / 総検査数) |
| n | エヌ | 1回あたりのサンプルサイズ(検査数) |
【例題】p管理図のUCL・LCLを求める
毎日100個ずつ検査を行い、20日間のデータを集計したところ、不適合品の合計は60個だった。p管理図のUCL、CL、LCLを求めよ。
解答
Step 1:p̄(平均不適合品率)を求める
p̄ = 60 / (100 × 20) = 60 / 2000 = 0.03(3%)
Step 2:√{p̄(1−p̄)/n}を計算する
= √{0.03 × 0.97 / 100}
= √{0.0291 / 100}
= √0.000291
= 0.01706
Step 3:UCL・CL・LCLを求める
UCL = 0.03 + 3 × 0.01706 = 0.03 + 0.0512 = 0.0812(8.12%)
CL = 0.03(3%)
LCL = 0.03 − 0.0512 = −0.0212 → 0(負なので0)
不良率や欠点数はマイナスにならないため、計算結果が負になった場合はLCL = 0とします。これは計数値管理図(p、np、c、u)すべてに共通するルールです。
【QC検定】np管理図・p管理図の作り方|不適合品数・不適合品率の管理 →
【計数値②】np管理図のUCL・LCLの求め方
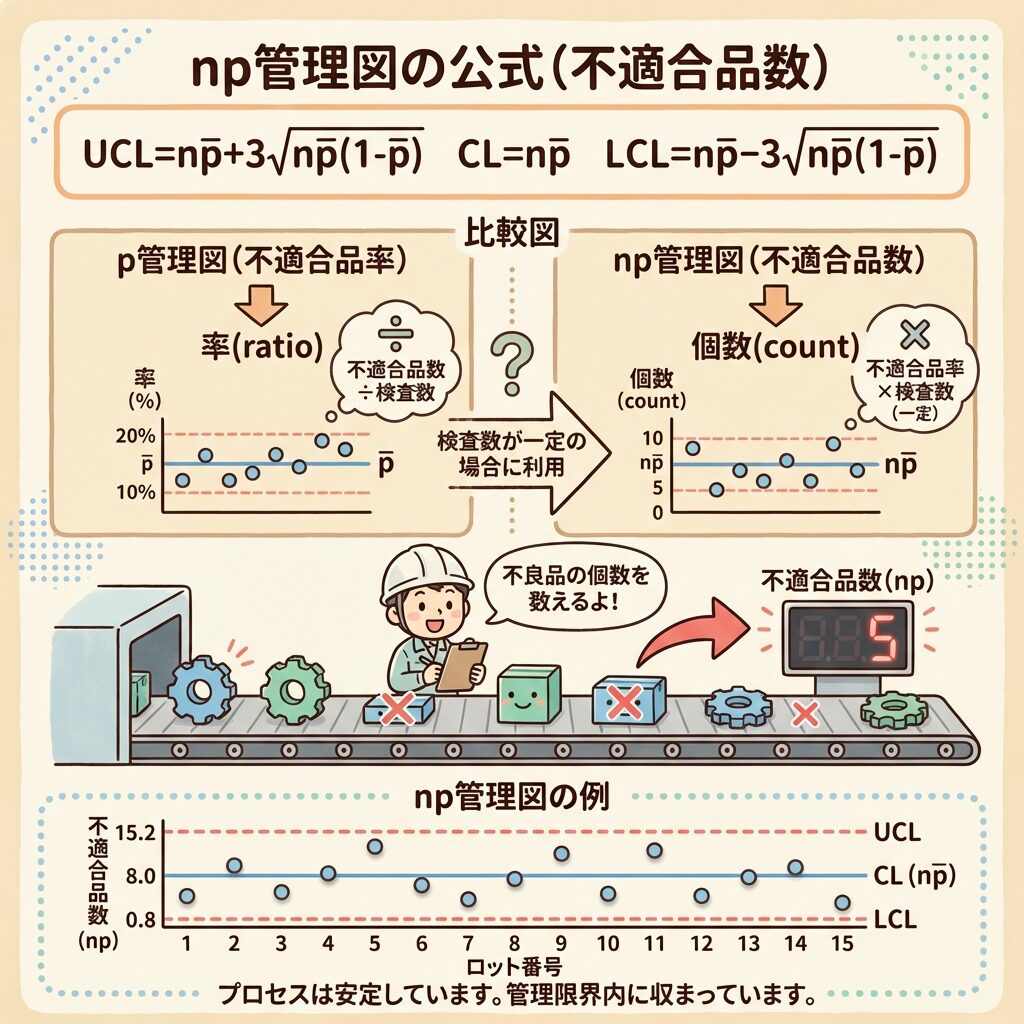
np管理図は、不適合品数(不良品の個数)を管理するための図です。p管理図が「率」で管理するのに対し、np管理図は「個数」で管理します。
- p管理図:サンプルサイズnが変動する場合(例:日によって検査数が違う)
- np管理図:サンプルサイズnが一定の場合(例:毎日100個検査)
np管理図の公式
※ LCLが負になる場合は LCL = 0 とする
【例題】np管理図のUCL・LCLを求める
先ほどと同じデータ(n=100、p̄=0.03)を使って、np管理図のUCL、CL、LCLを求めよ。
解答
Step 1:np̄(平均不適合品数)を求める
np̄ = 100 × 0.03 = 3(個)
Step 2:√{np̄(1−p̄)}を計算する
= √{3 × 0.97}
= √2.91
= 1.706
Step 3:UCL・CL・LCLを求める
UCL = 3 + 3 × 1.706 = 3 + 5.12 = 8.12(個)
CL = 3(個)
LCL = 3 − 5.12 = −2.12 → 0(個)
公式をよく見ると、np管理図の値はp管理図の値をn倍したものになっています。
- p管理図のCL = 0.03 → np管理図のCL = 0.03 × 100 = 3
- p管理図のUCL = 0.0812 → np管理図のUCL = 0.0812 × 100 ≈ 8.12
【計数値③】c管理図のUCL・LCLの求め方
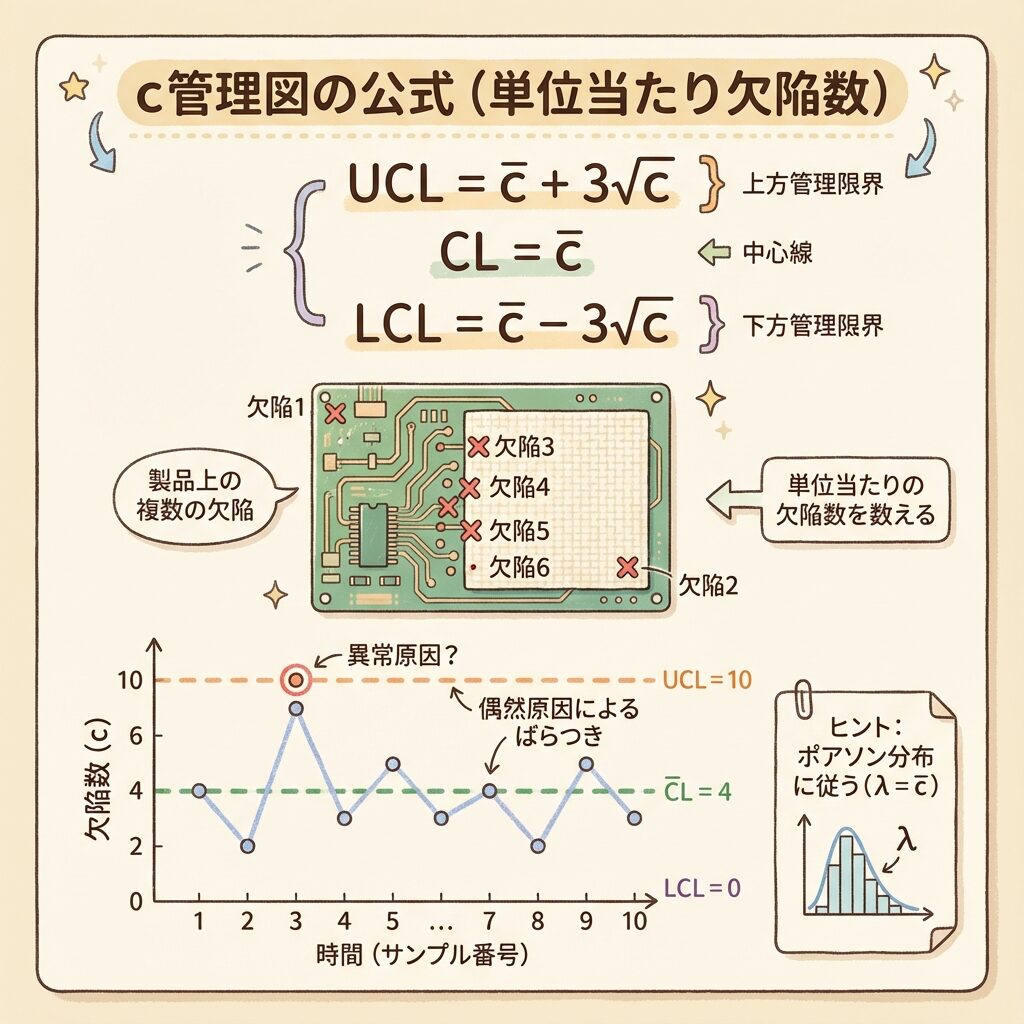
c管理図は、不適合数(欠点数)を管理するための図です。「不適合品」ではなく「不適合(欠点)」であることに注意してください。
- 不適合品:欠点が1つでもある製品のこと(良品 or 不良品)
- 不適合(欠点):製品1つあたりの欠点の数(傷の数、気泡の数など)
例:1枚の布に傷が3箇所ある → 不適合品は1枚、不適合数は3
c管理図の公式
※ LCLが負になる場合は LCL = 0 とする
c管理図はポアソン分布に基づいています。ポアソン分布では「平均=分散」という性質があるため、分散の平方根(標準偏差)は√c̄となり、公式がシンプルになります。
【例題】c管理図のUCL・LCLを求める
一定面積の布を20枚検査したところ、欠点数の合計は80個だった。c管理図のUCL、CL、LCLを求めよ。
解答
Step 1:c̄(平均欠点数)を求める
c̄ = 80 / 20 = 4(個/枚)
Step 2:√c̄を計算する
√c̄ = √4 = 2
Step 3:UCL・CL・LCLを求める
UCL = 4 + 3 × 2 = 10(個)
CL = 4(個)
LCL = 4 − 3 × 2 = −2 → 0(個)
【QC検定】c管理図・u管理図の作り方|不適合数の管理方法 →
【計数値④】u管理図のUCL・LCLの求め方
u管理図は、単位あたりの不適合数を管理するための図です。c管理図との違いは、検査する面積(単位)がサンプルごとに異なる場合に使う点です。
- c管理図:検査単位(面積・長さなど)が一定の場合
- u管理図:検査単位が変動する場合
例:布の検査で「今日は10m²、明日は15m²」のように面積が異なる → u管理図
u管理図の公式
※ LCLが負になる場合は LCL = 0 とする
※ nはサンプルごとに異なるため、管理限界線は階段状になることがある
記号の意味
| 記号 | 読み方 | 意味 |
|---|---|---|
| ū | ユーバー | 平均単位欠点数(= 総欠点数 / 総検査単位数) |
| n | エヌ | 各サンプルの検査単位数(サンプルごとに異なる場合あり) |
【例題】u管理図のUCL・LCLを求める
布の検査で、単位欠点数の平均がū=2.0(個/m²)だった。検査面積n=4m²のサンプルに対するUCL、CL、LCLを求めよ。
解答
Step 1:√(ū/n)を計算する
= √(2.0 / 4)
= √0.5
= 0.707
Step 2:UCL・CL・LCLを求める
UCL = 2.0 + 3 × 0.707 = 2.0 + 2.12 = 4.12(個/m²)
CL = 2.0(個/m²)
LCL = 2.0 − 2.12 = −0.12 → 0(個/m²)
u管理図では、サンプルごとに検査単位数nが異なる場合、管理限界線もサンプルごとに変わります(階段状の管理限界線になる)。計算問題では「n=○のとき」と指定されることが多いです。
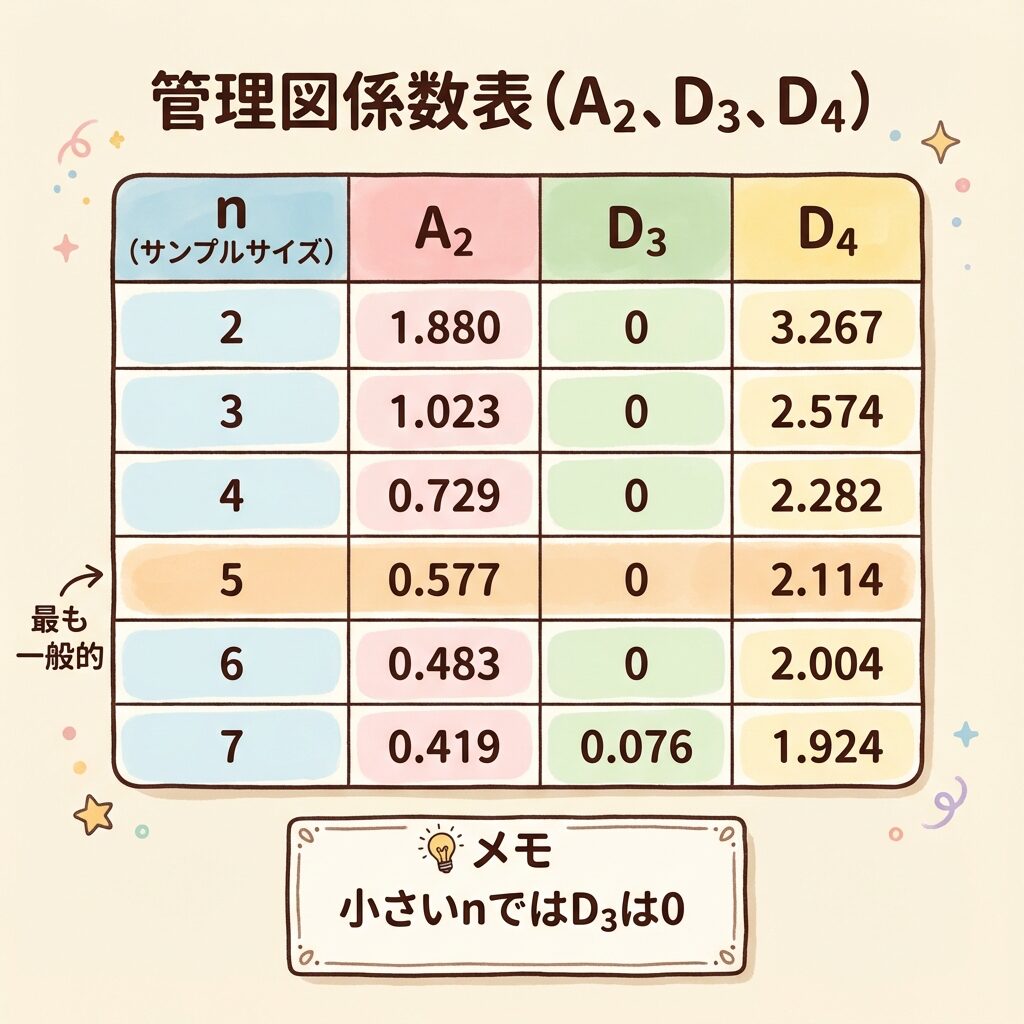
管理図の係数表(A₂・D₃・D₄)完全版
計量値の管理図(X̄-R管理図)で使う係数表です。QC検定では問題文中に与えられることが多いですが、どの係数をどこで使うかは覚えておく必要があります。
管理図用係数表
| n | A₂ | D₃ | D₄ | d₂ |
|---|---|---|---|---|
| 2 | 1.880 | − | 3.267 | 1.128 |
| 3 | 1.023 | − | 2.575 | 1.693 |
| 4 | 0.729 | − | 2.282 | 2.059 |
| 5 | 0.577 | − | 2.115 | 2.326 |
| 6 | 0.483 | − | 2.004 | 2.534 |
| 7 | 0.419 | 0.076 | 1.924 | 2.704 |
| 8 | 0.373 | 0.136 | 1.864 | 2.847 |
| 9 | 0.337 | 0.184 | 1.816 | 2.970 |
| 10 | 0.308 | 0.223 | 1.777 | 3.078 |
係数の使い分け早見表
| 係数 | 使う場面 | 公式での使い方 |
|---|---|---|
| A₂ | X̄管理図の管理限界 | UCL/LCL = X̿ ± A₂R̄ |
| D₃ | R管理図のLCL | LCL = D₃R̄(n≦6では存在しない) |
| D₄ | R管理図のUCL | UCL = D₄R̄ |
| d₂ | σの推定 | σ̂ = R̄ / d₂(工程能力指数の計算などで使用) |
QC検定ではサンプルサイズn=5の問題が頻出です。以下の値だけは覚えておくと便利です:
- A₂ = 0.577(約0.58)
- D₄ = 2.115(約2.1)
- D₃ = −(存在しない → LCLなし)
【QC検定】管理図の係数表A₂・D₃・D₄とは?意味と使い方を完全解説 →
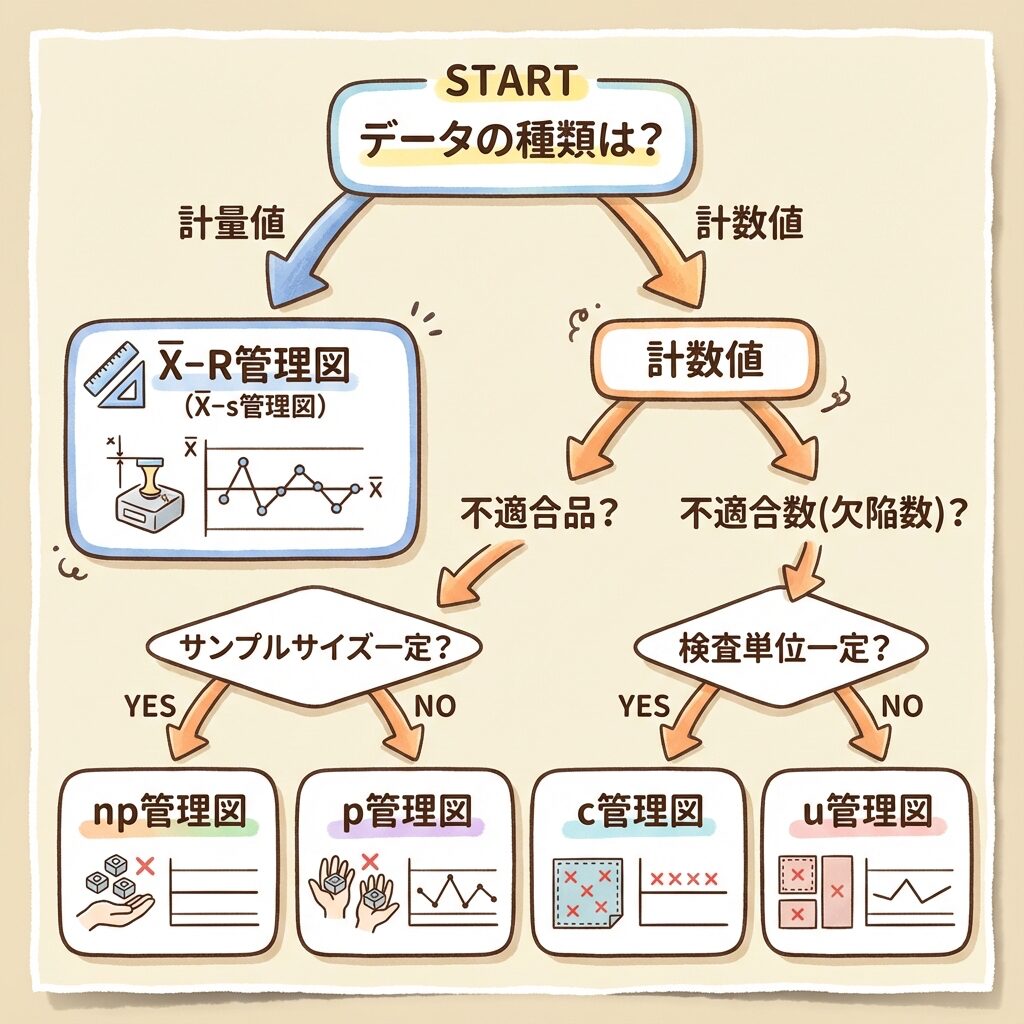
【フローチャート】どの管理図を使えばいい?
管理図の選択で迷ったときは、以下のフローチャートに従って判断しましょう。
(長さ・重さ・時間など測定値)
(個数・欠点数など数えた値)
- p = proportion(割合)→ 不適合品率
- np = n × p(サンプル数 × 割合)→ 不適合品数
- c = count(数える)→ 不適合数(一定面積)
- u = unit(単位あたり)→ 単位あたりの不適合数