Cp=Cpkのとき平均は問題ない？工程能力指数の「かたより度k」で改善ポイントを見抜く方法

工程能力指数CpとCpkを計算したあと、こんな経験はありませんか？

「Cp = 0.90、Cpk = 0.90 か…。どちらも1未満だから工程能力不足なのはわかる。でも、平均とばらつき、どっちを改善すればいいの？」

あるいは、

「Cp = 2.27、Cpk = 0.72 って、Cpは高いのにCpkは低い。これって結局、何が悪いの？」

実は、CpとCpkの「関係性」を見れば、改善すべきポイントは一発でわかります。

この記事では、「かたより度k」という概念を使って、CpとCpkの関係から「平均を直すべきか、ばらつきを直すべきか」を判断する方法を、初心者向けにやさしく解説します。

まずは復習：CpとCpkは「何を見ているか」が違う

改善ポイントを見抜く前に、CpとCpkの違いを改めて整理しておきましょう。

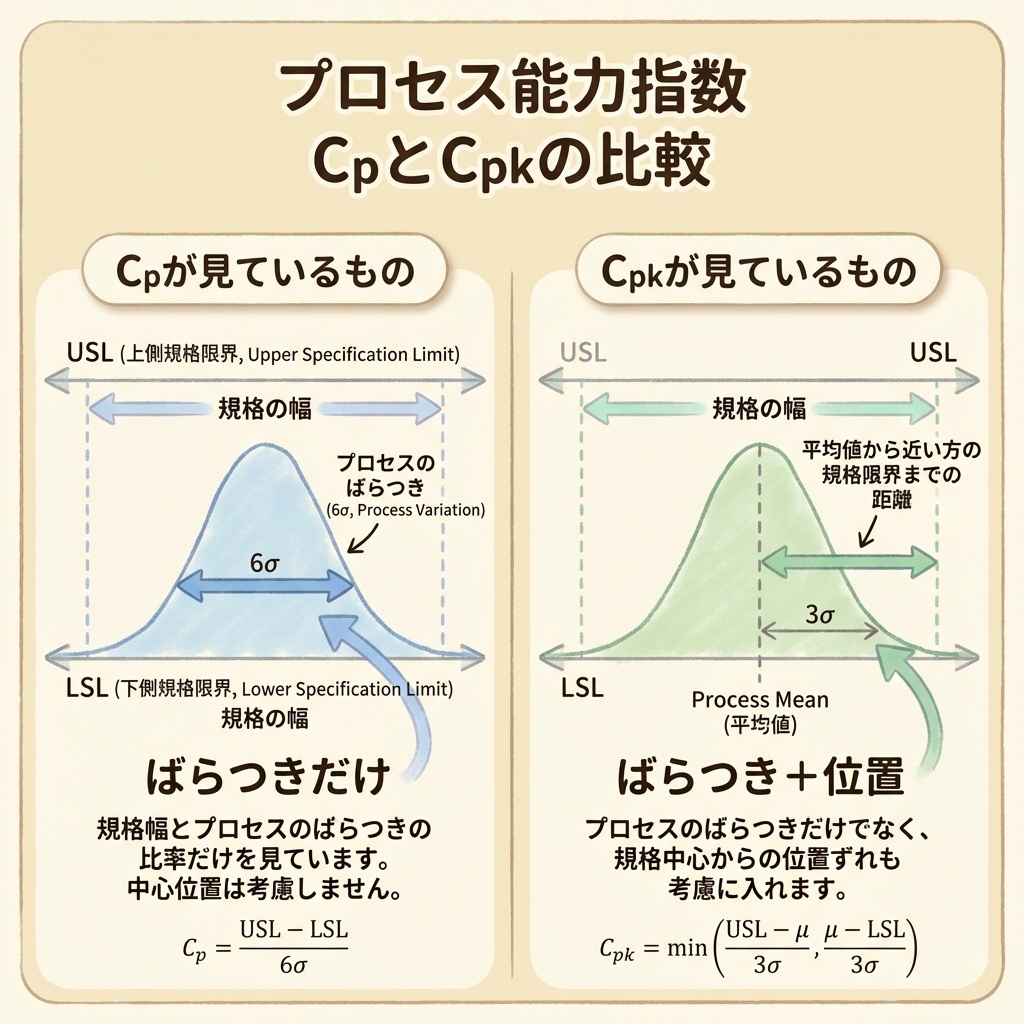
🎯 Cpは「ばらつき」だけを見ている

Cpの公式を思い出してください。

この式には「平均（μ̂）」が登場しません。つまり、Cpは「データが規格幅に対してどれだけ散らばっているか」だけを評価しています。

平均が規格の中心にあろうが、端に寄っていようが、Cpの値は変わりません。

🎯 Cpkは「ばらつき」と「平均のずれ」の両方を見ている

一方、Cpkの公式はこうです。

Cpkの式には「平均（μ̂）」が入っています。つまり、Cpkは「ばらつき」だけでなく、「平均が規格の中心からどれだけずれているか」も評価しているのです。

📊 CpとCpkの違いを表で整理

指標	何を評価するか	平均のずれを考慮するか
Cp	ばらつきのみ	❌ しない
Cpk	ばらつき＋平均のずれ	✅ する

「かたより度k」を理解する──的当てゲームでイメージ

CpとCpkの関係を理解するカギは、「かたより度k」という指標です。

これを「的当てゲーム」でイメージしてみましょう。

🎯 的当てゲームで考える

ダーツの的をイメージしてください。

• 的の中心 = 規格の中心（理想の値）
• 矢が刺さった位置 = 実際の製品データ
• 矢の散らばり具合 = ばらつき（σ）
• 矢の中心と的の中心のずれ = かたより（平均のずれ）

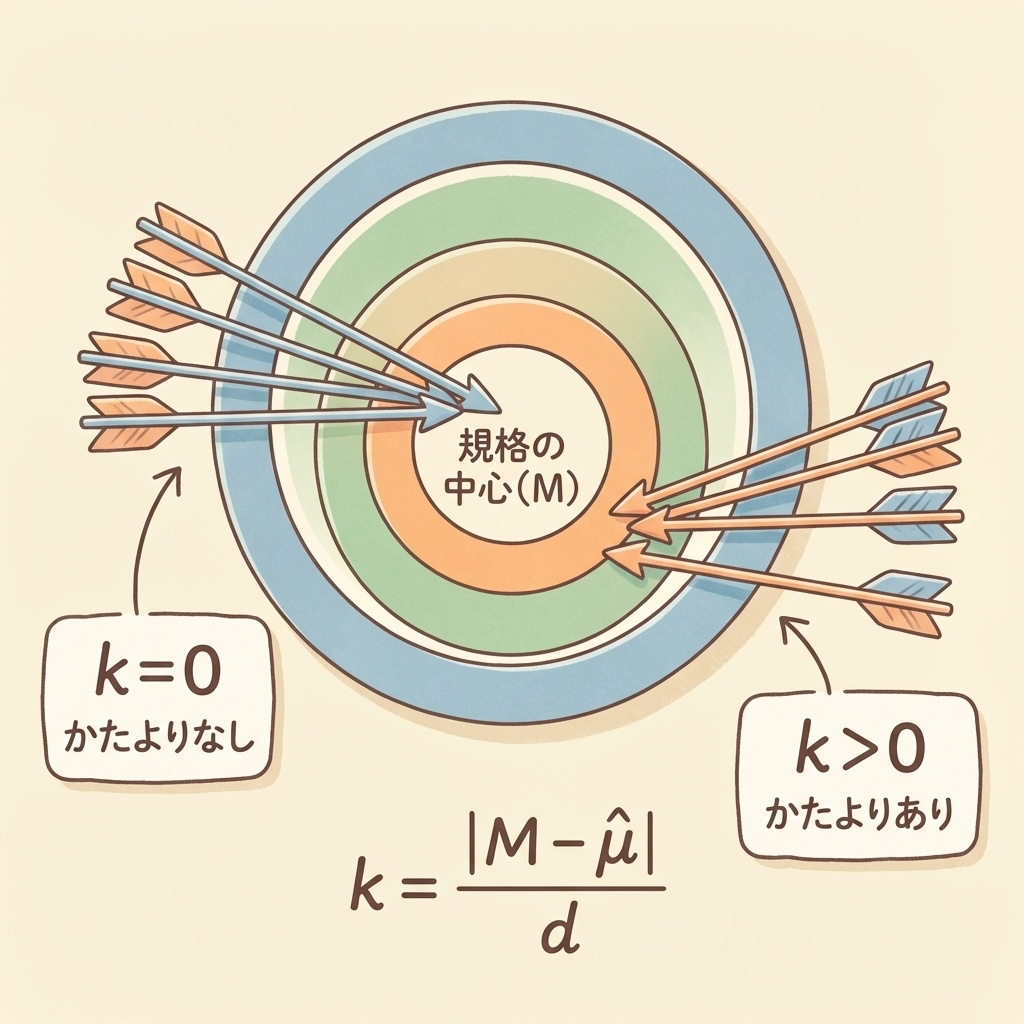
パターンA：矢が的の中心に集まっている（k = 0）

矢がすべて的の真ん中付近に刺さっている状態。これは「平均が規格の中心にある」ことを意味します。

このとき、かたより度 k = 0 です。

パターンB：矢がまとまっているが、中心からずれている（k > 0）

矢は小さくまとまっているけど、的の中心ではなく右上に集中している状態。これは「ばらつきは小さいが、平均がずれている」ことを意味します。

このとき、かたより度 k > 0 です。

📐 かたより度kの公式

かたより度kは、次の式で計算します。

つまり、kは「平均が規格の中心からどれだけずれているか」を0〜1の範囲で表した指標です。

kの値	意味
k = 0	平均が規格の中心にピッタリ（かたよりなし）
0 < k < 1	平均が規格の中心からずれている
k = 1	平均が規格の上限または下限と一致（最悪）

CpとCpkをつなぐ魔法の公式：Cpk = (1−k) × Cp

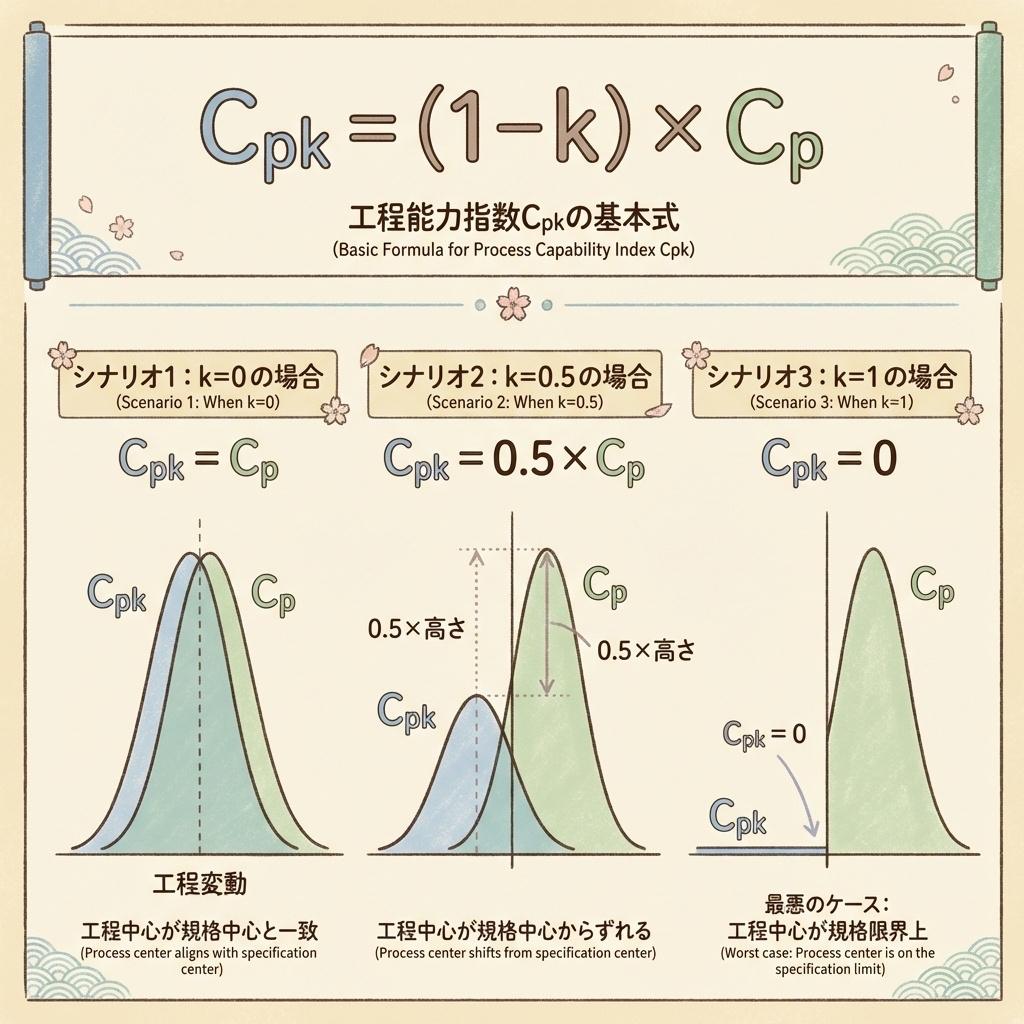
ここからが本題です。CpとCpkには、次の関係式が成り立ちます。

この式は、「Cpkは、Cpから"かたより分"を引いたもの」という意味です。

🔢 3つのパターンで理解する

パターン①：k = 0 のとき（かたよりなし）

k = 0 を式に代入すると：

Cpk = (1 − 0) × Cp = Cp

つまり、平均が規格の中心にあるとき、Cp = Cpk になります。

パターン②：k = 0.5 のとき（中程度のかたより）

k = 0.5 を式に代入すると：

Cpk = (1 − 0.5) × Cp = 0.5 × Cp

Cpkは、Cpの半分になります。

パターン③：k = 1 のとき（最大のかたより）

k = 1 を式に代入すると：

Cpk = (1 − 1) × Cp = 0

平均が規格の限界値と一致すると、Cpkは0になります。いくらばらつきが小さくても（Cpが高くても）、平均がずれていると工程能力は失われます。

🔄 逆算でkを求める

CpとCpkの値がわかれば、かたより度kを逆算できます。

この式を使えば、CpとCpkの値を見るだけで、平均のずれ具合を数値で把握できます。

【ケーススタディ①】Cp = Cpk のとき：ばらつきを改善せよ

それでは、具体的な数値で考えてみましょう。

📊 ケース①のデータ

特性	Cp	Cpk
重量	0.90	0.90

🔍 分析してみよう

Step 1：CpとCpkを比較する

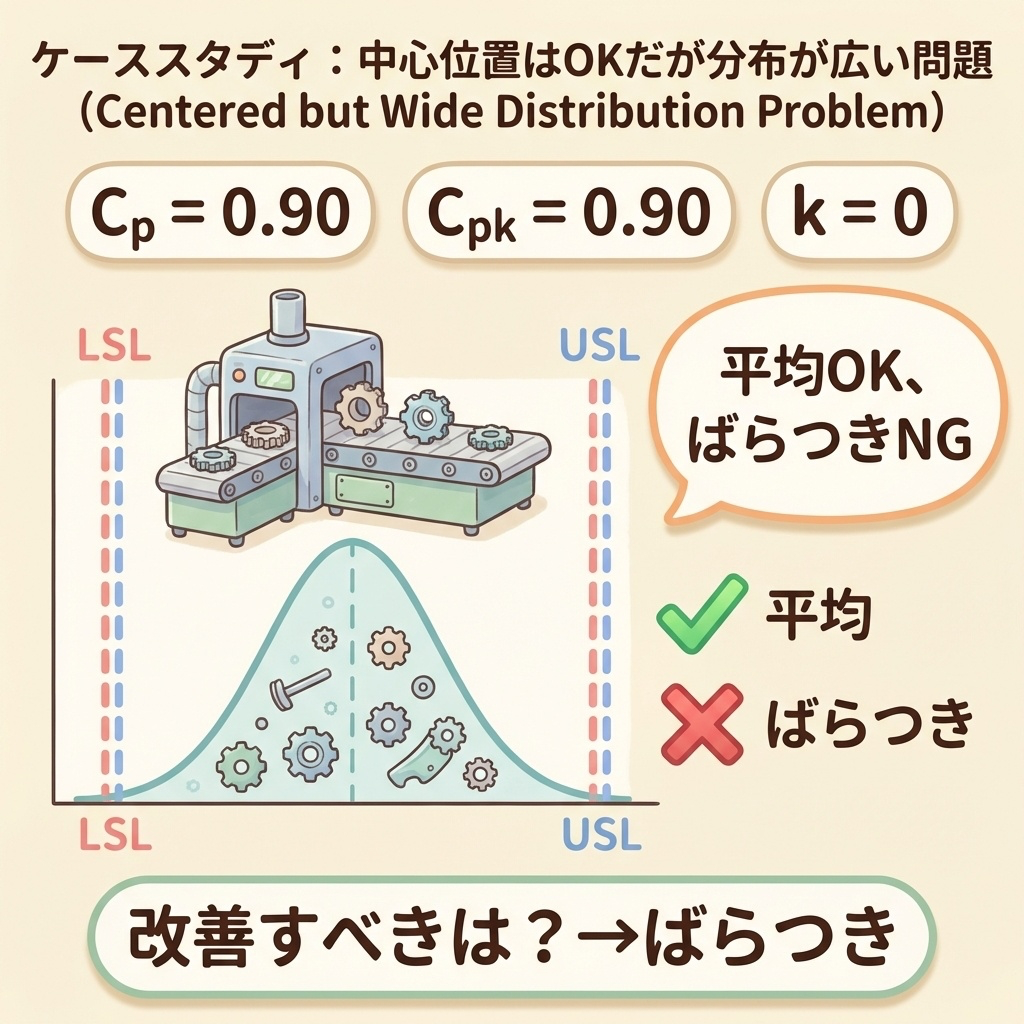
Cp = 0.90、Cpk = 0.90 なので、Cp = Cpk です。

Step 2：かたより度kを計算する

k = 1 − (Cpk / Cp) = 1 − (0.90 / 0.90) = 1 − 1 = 0

Step 3：診断結果

🛠️ 改善すべきポイント

平均は問題ないので、「ばらつき」を小さくすることに集中すべきです。

具体的には：

• 製造条件のばらつき要因を特定する（4M分析）
• 設備の精度を上げる
• 作業の標準化を徹底する
• 原材料のばらつきを抑える

【ケーススタディ②】Cp > Cpk のとき：平均を改善せよ

次に、CpとCpkが異なるケースを見てみましょう。

📊 ケース②のデータ

特性	Cp	Cpk
厚み	2.27	0.72

🔍 分析してみよう

Step 1：CpとCpkを比較する

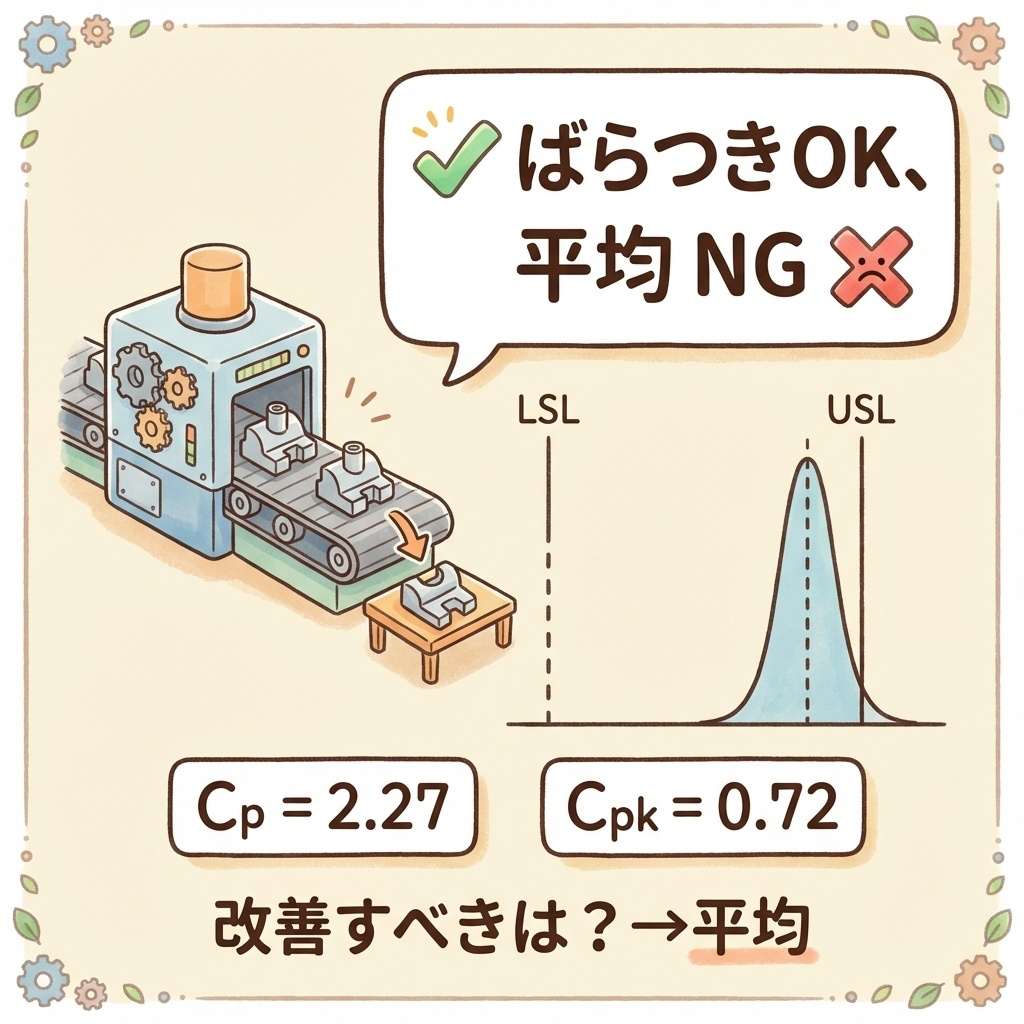
Cp = 2.27、Cpk = 0.72 なので、Cp >> Cpk（Cpの方がずっと大きい）です。

Step 2：かたより度kを計算する

k = 1 − (Cpk / Cp) = 1 − (0.72 / 2.27) = 1 − 0.317 ≈ 0.68

Step 3：診断結果

🛠️ 改善すべきポイント

ばらつきは問題ないので、「平均」を規格の中心に近づけることに集中すべきです。

具体的には：

• 設備の設定値（温度、圧力など）を調整する
• 工程の狙い値を見直す
• 測定器の校正を確認する

平均を調整するだけで、Cpkは大幅に改善します。ばらつきを小さくする（難しい）よりも、平均を調整する（比較的簡単）方が効率的です。

【判断フローチャート】改善ポイントを一発で見抜く

ここまでの内容を、判断フローチャートにまとめました。

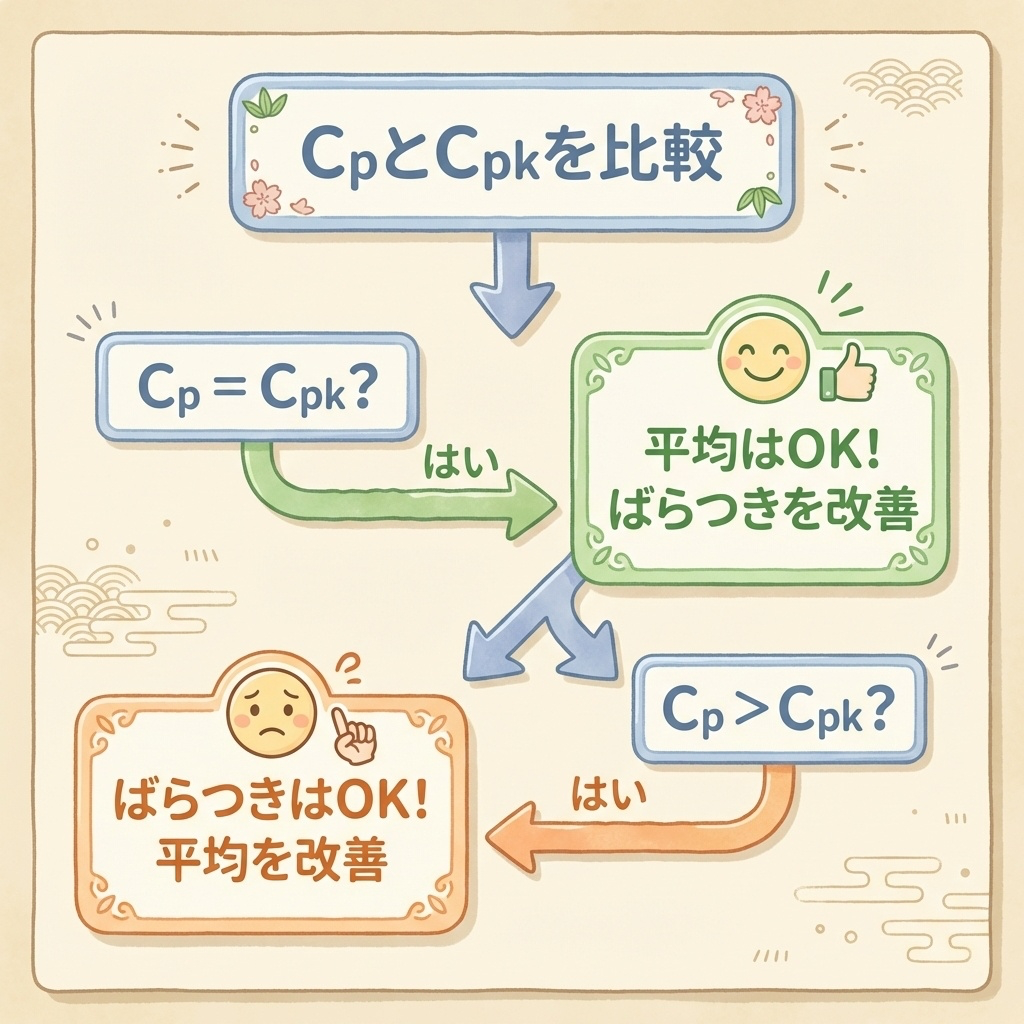
📋 CpとCpkから改善ポイントを判断するフロー

📊 判断基準の早見表

CpとCpkの関係	かたより度k	平均の状態	ばらつきの状態	改善ポイント
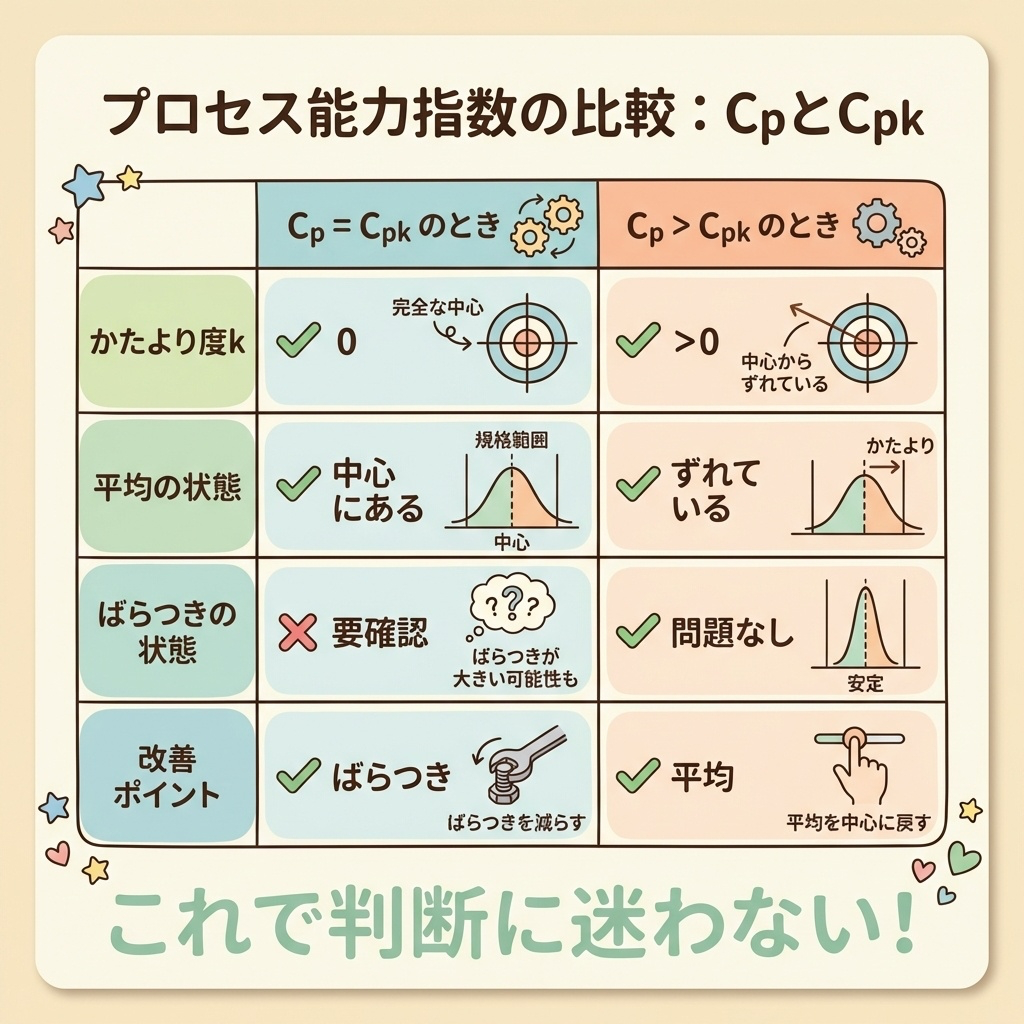
Cp = Cpk	0	✅ 中心にある	❌ 要確認	ばらつき
Cp > Cpk	> 0	❌ ずれている	✅ 問題なし	平均

まとめ：CpとCpkの関係から改善ポイントを見抜く

この記事の内容を整理します。

CpとCpkの値を見たときに、「両方低いから両方改善」と短絡的に考えないことが重要です。

特に、Cp = Cpk のときは「平均は規格の中心にある」ことを意味します。この場合、平均を調整しても効果はありません。ばらつきを小さくすることに集中すべきです。

逆に、Cpが高いのにCpkが低い場合は、平均を調整するだけで大幅な改善が見込めます。ばらつきを小さくする（難しい・コストがかかる）よりも効率的です。