- スナバ回路の抵抗値とコンデンサ容量、どうやって決めればいいの?
- 計算式は見たことあるけど、なぜその値になるのかわからない…
- 部品を選ぶとき、何を基準にすればいいのか知りたい
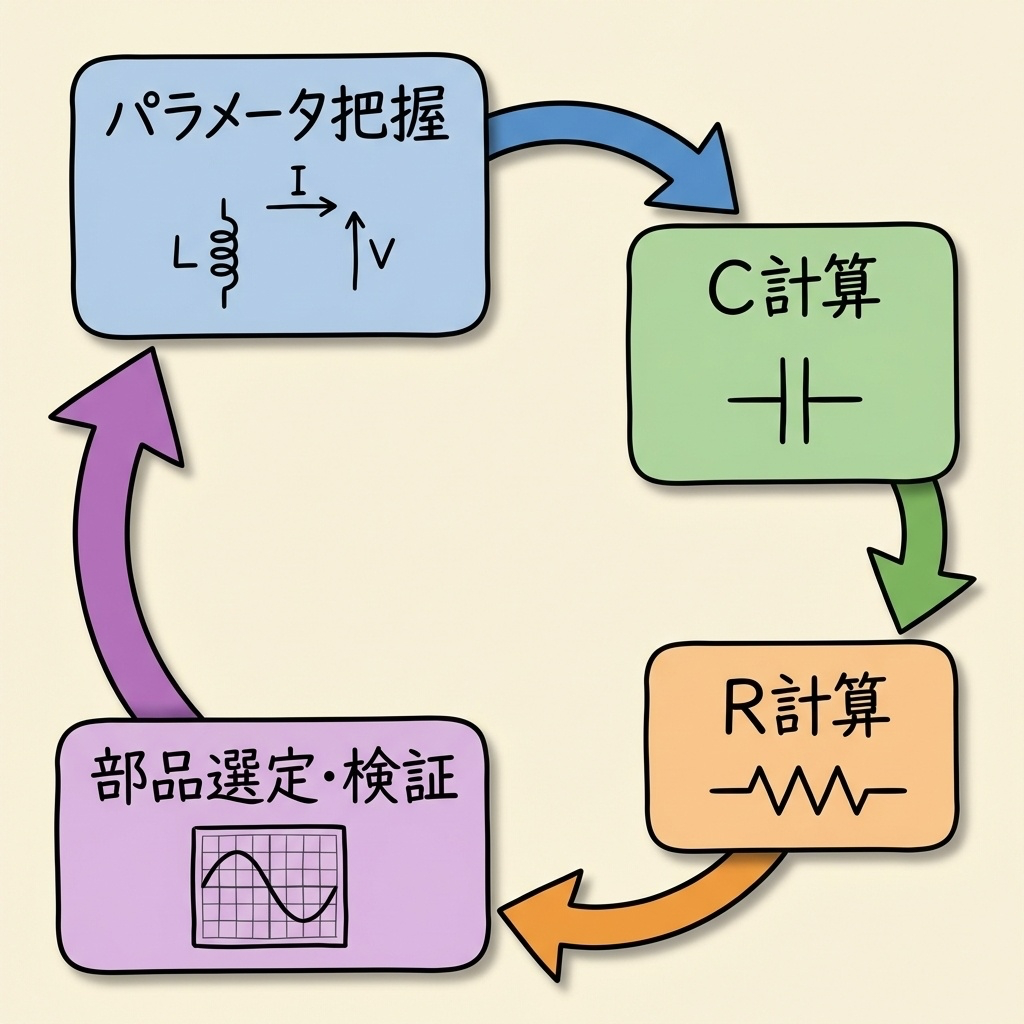
- RCスナバ回路がサージ電圧を抑える「仕組み」
- 抵抗値R・コンデンサ容量Cの計算式と導出過程
- 実務で使える部品選定のチェックポイント
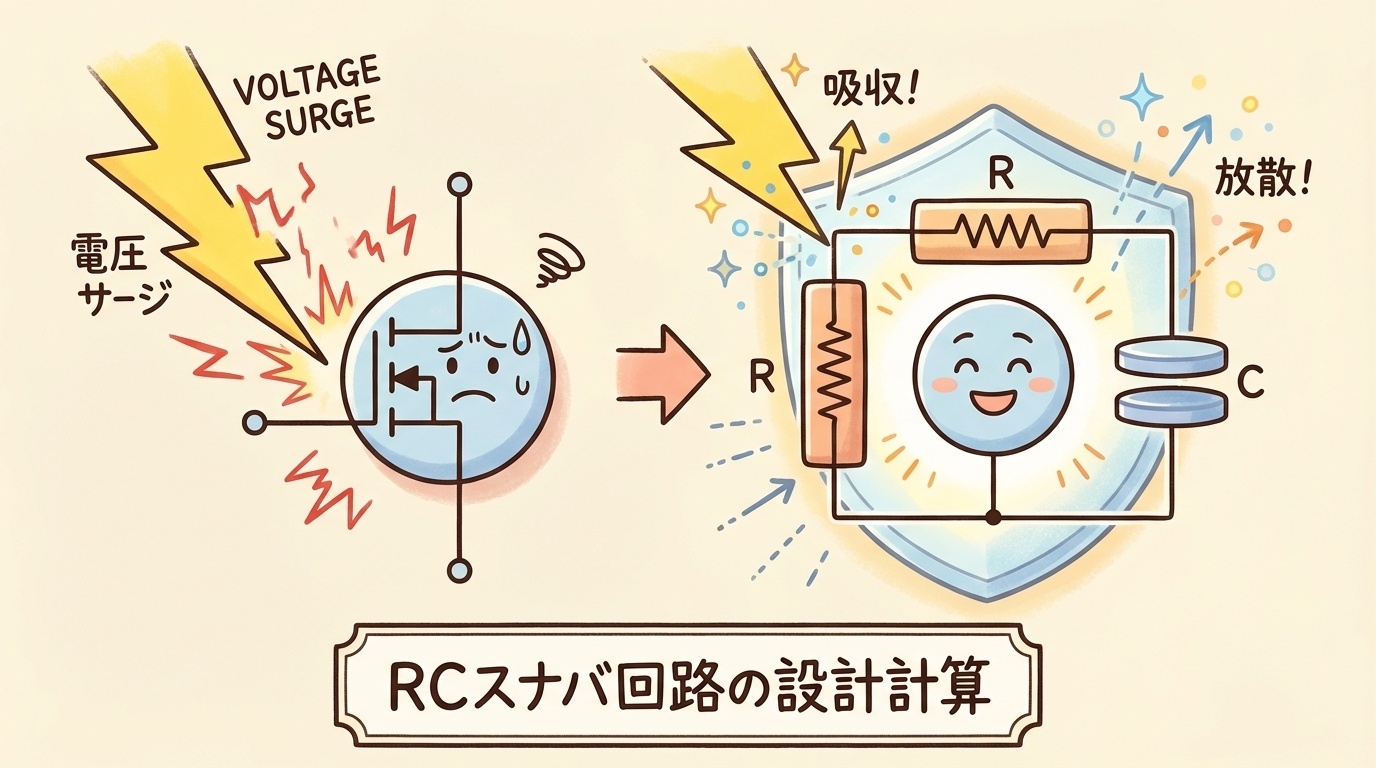
パワーエレクトロニクス回路を設計していると、必ず直面するのが「スイッチングサージ」の問題です。MOSFETやIGBTがOFFになる瞬間、配線のインダクタンスによって急激な電圧スパイクが発生し、素子を破壊してしまうことがあります。
この問題を解決するのが「RCスナバ回路」です。しかし、「抵抗とコンデンサを付ければいい」とわかっていても、その値をどう決めるかで悩む方が多いのではないでしょうか。
この記事では、RCスナバ回路の設計計算を「なぜその式になるのか」から丁寧に解説します。公式を暗記するのではなく、原理を理解して自分で設計できるようになりましょう。
目次
RCスナバ回路の役割をおさらい
まず、RCスナバ回路が何をしているのかを簡単におさらいしましょう。
サージ電圧が発生するメカニズム
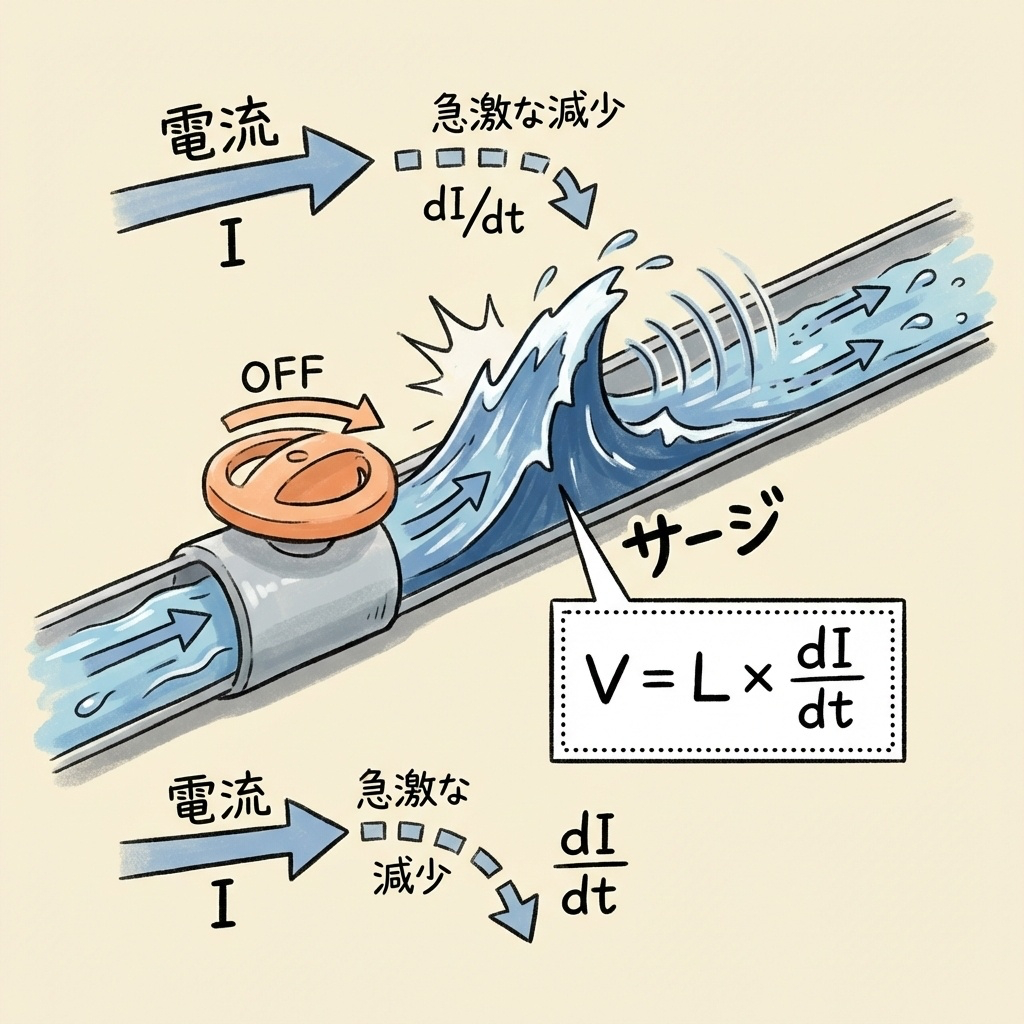
MOSFETやIGBTなどのスイッチング素子がOFFになると、それまで流れていた電流が急激に遮断されます。このとき、配線やプリント基板のパターンには寄生インダクタンス(L)が存在するため、以下の式でサージ電圧が発生します。
L:寄生インダクタンス [H]、dI/dt:電流の変化率 [A/s]
これを「水道管」で例えると、蛇口を急に閉めたときに「ドン!」と衝撃が来る現象(ウォーターハンマー)と同じです。流れていた水(電流)が急に止まると、その勢い(エネルギー)が行き場を失い、圧力スパイク(電圧スパイク)として現れます。
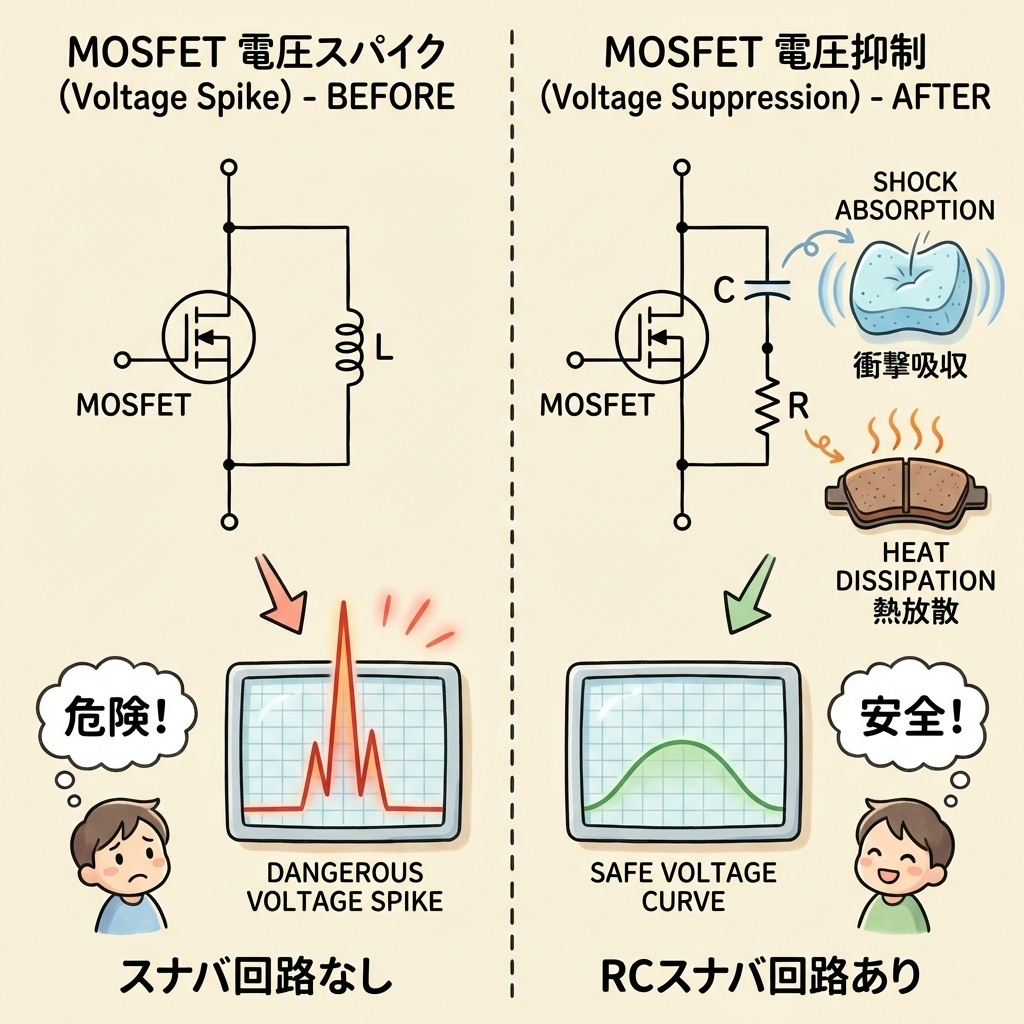
RCスナバ回路の「吸収」メカニズム
RCスナバ回路は、スイッチング素子と並列に接続します。素子がOFFになる瞬間、サージエネルギーはスナバコンデンサ(C)に吸収され、抵抗(R)で熱として消費されます。
コンデンサ(C)の役割
- サージエネルギーを一時的に「貯める」
- 電圧上昇の速度をゆっくりにする
- dV/dtを抑制する「クッション」
抵抗(R)の役割
- コンデンサに貯まったエネルギーを「消費」
- LC共振による振動を減衰させる
- ダンピング(制振)の役割
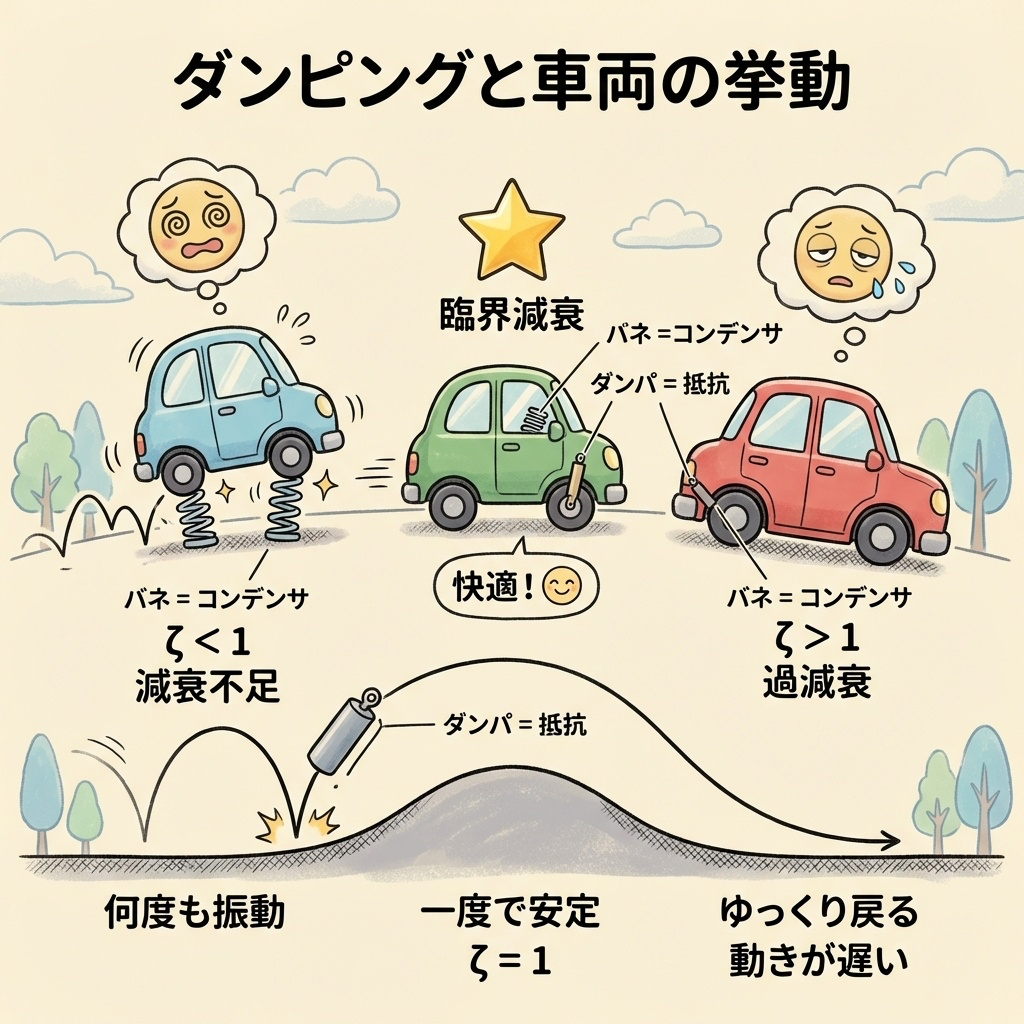
コンデンサは「衝撃吸収材(スポンジ)」、抵抗は「摩擦で熱に変える装置」と考えましょう。車のサスペンションに例えると、コンデンサがバネ、抵抗がショックアブソーバーです。両方がないと、いつまでも揺れ続けてしまいます。
RCスナバ回路の設計手順|全体の流れ
RCスナバ回路の設計は、以下の4ステップで進めます。最初に全体像を把握しておきましょう。
寄生インダクタンスL、スイッチング電流I、電源電圧Vなどを確認
サージエネルギーを吸収できる容量を算出
振動を適切に減衰させる抵抗値を算出
定格確認、損失計算、実機での動作確認
では、それぞれのステップを詳しく見ていきましょう。
STEP 1:回路パラメータの把握
設計を始める前に、以下のパラメータを把握する必要があります。
| パラメータ | 記号 | 単位 | 確認方法 |
|---|---|---|---|
| 寄生インダクタンス | L | nH〜μH | 実測 or 経験値(10〜100nH/cm) |
| スイッチング電流 | I | A | 回路仕様から |
| 電源電圧 | VDC | V | 回路仕様から |
| 素子の耐圧 | VDSS | V | データシートから |
| スイッチング周波数 | fsw | kHz | 回路仕様から |
| 許容サージ電圧 | Vmax | V | VDSS × 0.8 程度 |
寄生インダクタンスLは実測が難しいため、経験値を使うことが多いです。プリント基板のパターンは約10nH/cm、リード線は約10〜20nH/cmが目安です。主回路ループの総配線長から概算しましょう。
STEP 2:コンデンサ容量Cの計算
コンデンサ容量Cの設計には、2つのアプローチがあります。どちらの考え方も理解しておきましょう。
アプローチ①:エネルギー保存則から求める
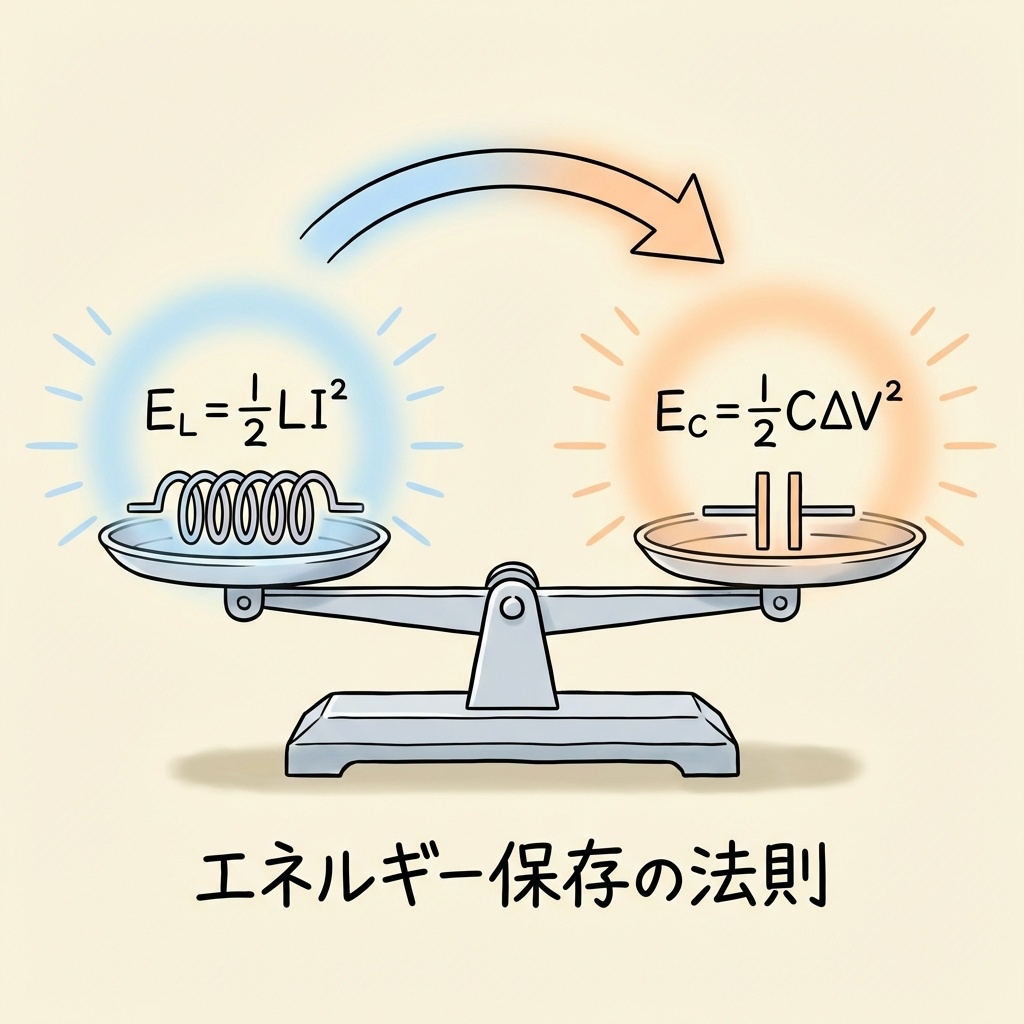
最も基本的な考え方は、「インダクタンスに蓄えられたエネルギーを、コンデンサで受け止める」というものです。
スイッチング素子がOFFになる瞬間、寄生インダクタンスLには以下のエネルギーが蓄えられています。
このエネルギーがすべてコンデンサに移動すると、コンデンサの電圧は上昇します。電圧上昇分を ΔV とすると、
エネルギー保存則 EL = EC から、コンデンサ容量Cは次のように求まります。
ΔV = Vmax − VDC(許容サージ電圧 − 電源電圧)
計算例①:エネルギー保存則
以下の条件でコンデンサ容量を計算してみましょう。
| 寄生インダクタンス L | 100 nH |
| スイッチング電流 I | 10 A |
| 電源電圧 VDC | 300 V |
| 許容サージ電圧 Vmax | 400 V |
【計算】
ΔV = 400 − 300 = 100 V
C = (100 × 10⁻⁹ × 10²) / 100²
C = (100 × 10⁻⁹ × 100) / 10000
C = 10 × 10⁻⁶ / 10⁴ = 1 × 10⁻⁹
∴ C = 1 nF(= 1000 pF)
アプローチ②:特性インピーダンスから求める(推奨)
実務でより一般的に使われるのが、LCの特性インピーダンスを基準にする方法です。
寄生インダクタンスLとスナバコンデンサCは、LC共振回路を形成します。この回路の特性インピーダンス Z₀は次のように定義されます。
スイッチング時のサージ電圧は、この特性インピーダンスと電流の積で決まります。
この式をCについて解くと、以下のようになります。
※アプローチ①と同じ式に帰着します(当然ですね!)
実は、LC共振回路ではエネルギーがLとCの間を行き来します。EL = EC(エネルギー保存)と Z₀ = √(L/C)(特性インピーダンス)は、同じ物理現象を異なる視点で見ているだけなのです。
STEP 3:抵抗値Rの計算
次に、スナバ抵抗Rの値を決めます。Rの役割は「LC共振の振動を減衰させる」ことです。
減衰の度合いを決める「減衰係数ζ」
RLC回路の振動の収まり具合は、減衰係数ζ(ゼータ)で表されます。
この減衰係数ζの値によって、回路の振動特性が大きく変わります。
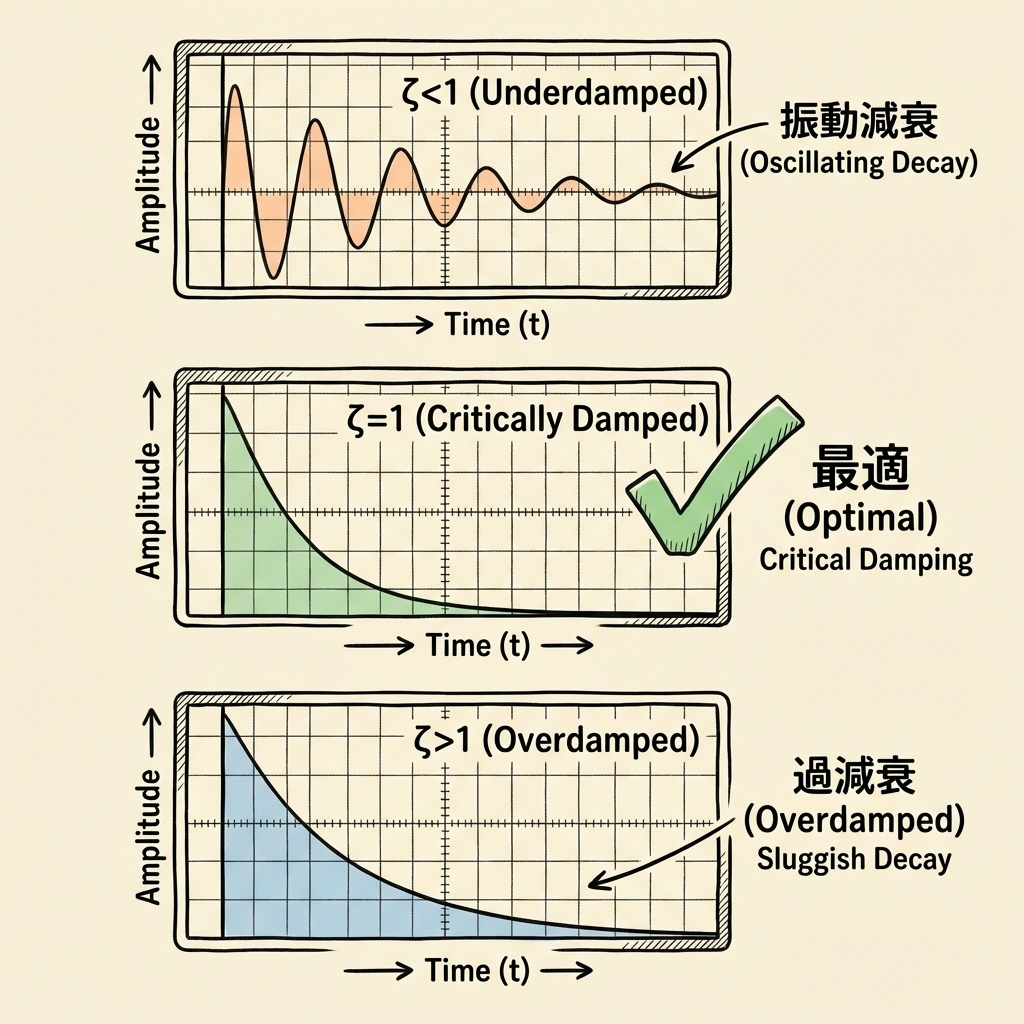
| 減衰係数 ζ | 状態 | 特徴 |
|---|---|---|
| ζ < 1 | 不足減衰 | 振動しながら収束(リンギングあり) |
| ζ = 1 | 臨界減衰 | 振動なしで最速収束(理想状態) |
| ζ > 1 | 過減衰 | 振動なしだが収束が遅い |
ζ < 1(不足減衰):段差を越えると、ボヨンボヨン揺れ続ける
ζ = 1(臨界減衰):段差を越えても、スッと1回で収まる(高級車の乗り心地)
ζ > 1(過減衰):ゆっくりしか戻らず、次の段差に対応できない
抵抗値Rの設計式
スナバ回路では、臨界減衰(ζ = 1)を目標に設計するのが一般的です。ζ = 1 の式をRについて解くと、
※ R = 2 × Z₀(特性インピーダンスの2倍)とも表現できます
実務では、臨界減衰の値を中心に0.5〜2倍の範囲で調整します。
| 調整方針 | Rの調整 | 効果 |
|---|---|---|
| リンギングを抑えたい | R を大きく | 減衰が強くなる(ζ↑) |
| スナバ損失を減らしたい | R を小さく | 損失は減るがリンギング増加 |
計算例②:抵抗値の算出
先ほどの計算例(L = 100nH、C = 1nF)で抵抗値を求めます。
【計算】
R = 2 × √(L / C)
R = 2 × √(100 × 10⁻⁹ / 1 × 10⁻⁹)
R = 2 × √100
R = 2 × 10
∴ R = 20 Ω
計算で R = 20Ω と出ても、実際にはオシロスコープで波形を見ながら10Ω〜47Ω 程度の範囲で微調整します。机上計算だけで完璧な値は出せないため、最終的には実測で詰めることが重要です。
STEP 4:部品の選定と検証
RとCの値が決まったら、実際の部品を選定します。ここで定格を間違えると部品が壊れるので、慎重に確認しましょう。
コンデンサの選定ポイント
| チェック項目 | 確認内容 | 推奨 |
|---|---|---|
| 定格電圧 | Vmax以上か | Vmax × 1.5倍以上 |
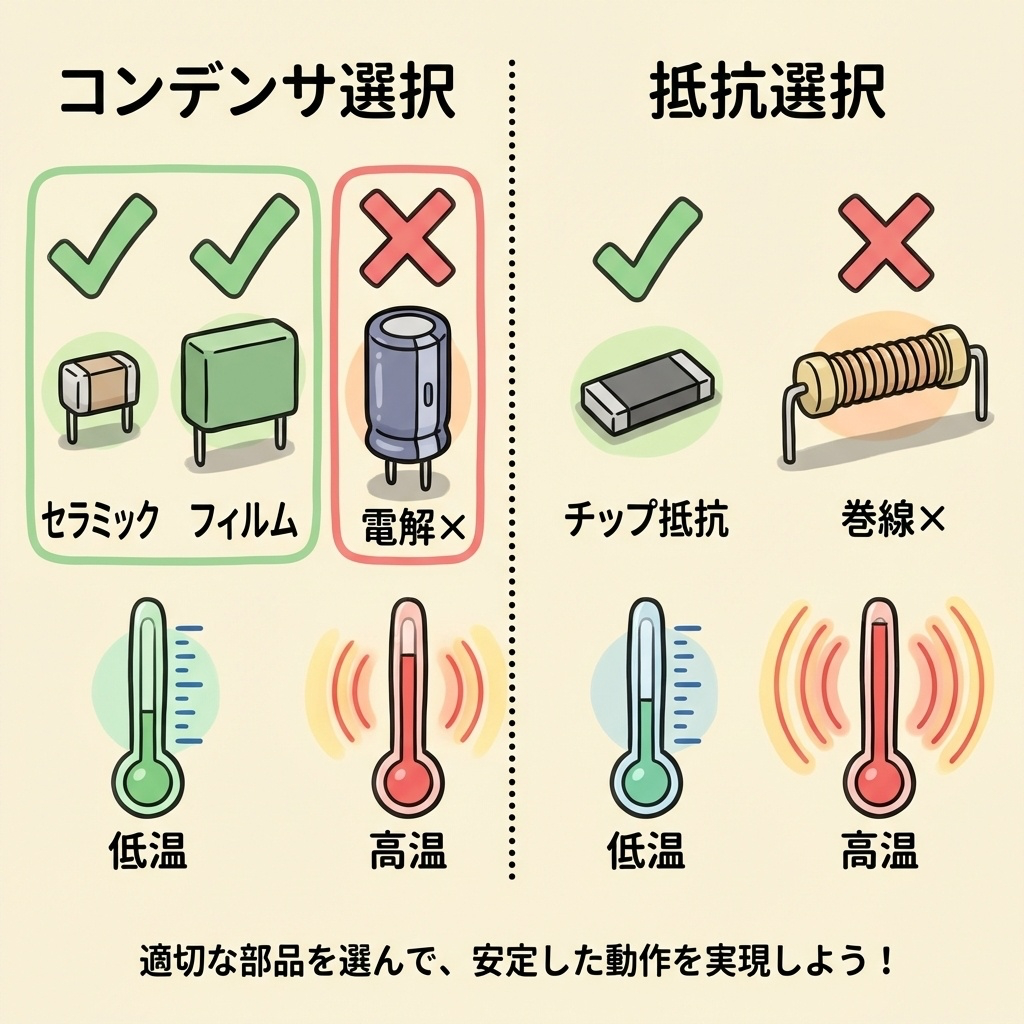
| 種類 | 高周波特性が良いか | セラミック or フィルム |
| ESR / ESL | 内部インピーダンスが低いか | 低ESR品を選定 |
| リップル電流 | 許容リップル電流以下か | データシートで確認 |
スナバ回路には電解コンデンサは不向きです。高周波でESRが高く、急峻な電流に対応できません。必ずセラミックコンデンサかフィルムコンデンサを使用してください。
抵抗の選定ポイント
抵抗の選定で最も重要なのは損失(発熱)です。スナバ抵抗は毎回のスイッチングでエネルギーを消費するため、発熱量を計算して定格電力を決める必要があります。
fsw:スイッチング周波数 [Hz]
計算例③:抵抗の損失計算
スイッチング周波数 fsw = 100kHz の場合の損失を計算します。
【条件】
C = 1nF、Vmax = 400V、fsw = 100kHz
【計算】
Psnub = 0.5 × 1 × 10⁻⁹ × 400² × 100 × 10³
Psnub = 0.5 × 1 × 10⁻⁹ × 160000 × 100000
Psnub = 0.5 × 16 × 10⁻⁹ × 10⁹
Psnub = 0.5 × 16 = 8
∴ Psnub = 8 W
8Wもの損失があるため、定格電力は最低でも2倍の16W以上の抵抗を選ぶ必要があります。小さな抵抗では発熱で壊れてしまいます。
| チェック項目 | 確認内容 | 推奨 |
|---|---|---|
| 定格電力 | Psnub 以上か | 計算値の2倍以上 |
| 種類 | 高周波・高電力対応か | 無誘導タイプ推奨 |
| インダクタンス | ESLが低いか | 巻線型は避ける |
巻線型(ワイヤーワウンド)抵抗は、コイルのようにインダクタンス成分を持っています。高周波で使うと、抵抗として機能しなくなるため、チップ抵抗や厚膜抵抗などの無誘導タイプを使用してください。
設計計算のまとめ|公式一覧
ここまでの設計計算を整理します。実務で使えるよう、公式をまとめておきましょう。
📋 RCスナバ回路 設計公式チートシート
コンデンサ容量 C
ΔV = Vmax − VDC
抵抗値 R(臨界減衰)
実務では 0.5R 〜 2R の範囲で調整
特性インピーダンス Z₀
R = 2 × Z₀ で臨界減衰
スナバ損失 Psnub
抵抗の定格は Psnub × 2倍以上
設計時の注意点とトラブルシューティング
よくある失敗パターンと対策
❌ 失敗①:Cが小さすぎる
症状:サージ電圧が十分に抑えられない
対策:Cを大きくする(ΔVを小さくする)
❌ 失敗②:Cが大きすぎる
症状:損失が増大、抵抗が過熱
対策:Cを小さく、または抵抗の定格を上げる
❌ 失敗③:Rが小さすぎる
症状:リンギング(振動)が収まらない
対策:Rを大きくする(減衰を強める)
❌ 失敗④:Rが大きすぎる
症状:スナバが効かない(Cに電荷が溜まらない)
対策:Rを小さくする
机上計算はあくまで「出発点」です。最終的にはオシロスコープで波形を見ながらR・Cを調整してください。特にLの見積もりは誤差が大きいため、計算通りにいかないことが多いです。
まとめ
RCスナバ回路の設計計算について、原理から実務のポイントまで解説しました。
📌 この記事のポイント
- コンデンサ C はサージエネルギーを吸収する(C = L × I² / ΔV²)
- 抵抗 R は振動を減衰させる(R = 2√(L/C) で臨界減衰)
- 損失計算 を忘れずに(P = ½ × C × V² × fsw)
- 部品選定では定格と種類に注意(セラミックC、無誘導R)
- 最終調整はオシロスコープで実測しながら行う
スナバ回路は「付ければ終わり」ではなく、適切な設計と調整が必要です。この記事の計算式を出発点として、実機で波形を確認しながら最適化してください。
パワーエレクトロニクス設計は奥が深いですが、一つずつ理解していけば必ず身につきます。ぜひ関連記事も参考にして、設計スキルを磨いていってください。
📚 次に読むべき記事
スナバ回路の基本原理を復習したい方はこちら
スイッチング素子の駆動回路について学ぶ
基板設計でノイズを抑える配線テクニック