「管理図の勉強を始めたけど、そもそも"バラつき"って何?」
「標準偏差とか正規分布とか、いきなり出てきて混乱する…」
管理図や工程能力指数を学ぶ前に、こんな壁にぶつかっていませんか?
大丈夫です。この記事を読めば、品質管理の「超基本」がスッキリ分かります。
📌 この記事で分かること
- バラつきとは何か(お菓子工場でイメージ)
- バラつきがなぜ問題なのか
- 平均・標準偏差の意味(中学レベルでおさらい)
- 正規分布と3σの意味
- 管理図・工程能力指数へのつながり
品質管理の世界では、「バラつき」が最大の敵です。
でも、「バラつき」って言われても、ピンとこないですよね。
この記事では、お菓子工場を例に、バラつきの意味と、それを数値で表す方法を中学生でもわかるレベルで解説します。
ここを押さえておけば、管理図の勉強がグッと楽になりますよ!
目次
🍪 バラつきとは?|お菓子工場でイメージしよう
結論から言うと、バラつき = 「同じはずなのに、違いが出ること」です。
🔹 たとえ話:クッキー工場
あなたがクッキー工場の工場長だとしましょう。
このクッキーは「1枚10g」で販売しています。
でも、実際に作ってみると…
🍪 9.8g 🍪 10.2g 🍪 9.5g 🍪 10.1g 🍪 10.4g
↑ 同じ機械で作っているのに、重さがバラバラ!
これが「バラつき」です。
同じ機械、同じ材料、同じ作り方なのに、完全に同じ製品は作れないのです。
これは避けられない事実で、どんな工場でも必ず起こります。

🔹 バラつきはなぜ起こる?
バラつきの原因は、大きく2種類に分けられます。
| 種類 | 意味 | クッキー工場での例 |
|---|---|---|
| 偶然原因 | 避けられない小さな変動 | 気温のわずかな変化、材料の微妙な違い |
| 異常原因 | 取り除ける特定の原因 | 機械の故障、作業者のミス、材料の不良 |
偶然原因によるバラつきは「仕方ない」もの。ゼロにはできません。
異常原因によるバラつきは「見つけて取り除く」もの。
品質管理の目的は、異常原因を早く見つけて対処することです。
😱 バラつきが大きいと何が困る?
「多少バラついても、大体10gなら問題ないのでは?」
そう思うかもしれません。
でも、バラつきが大きくなると、大変なことが起こります。
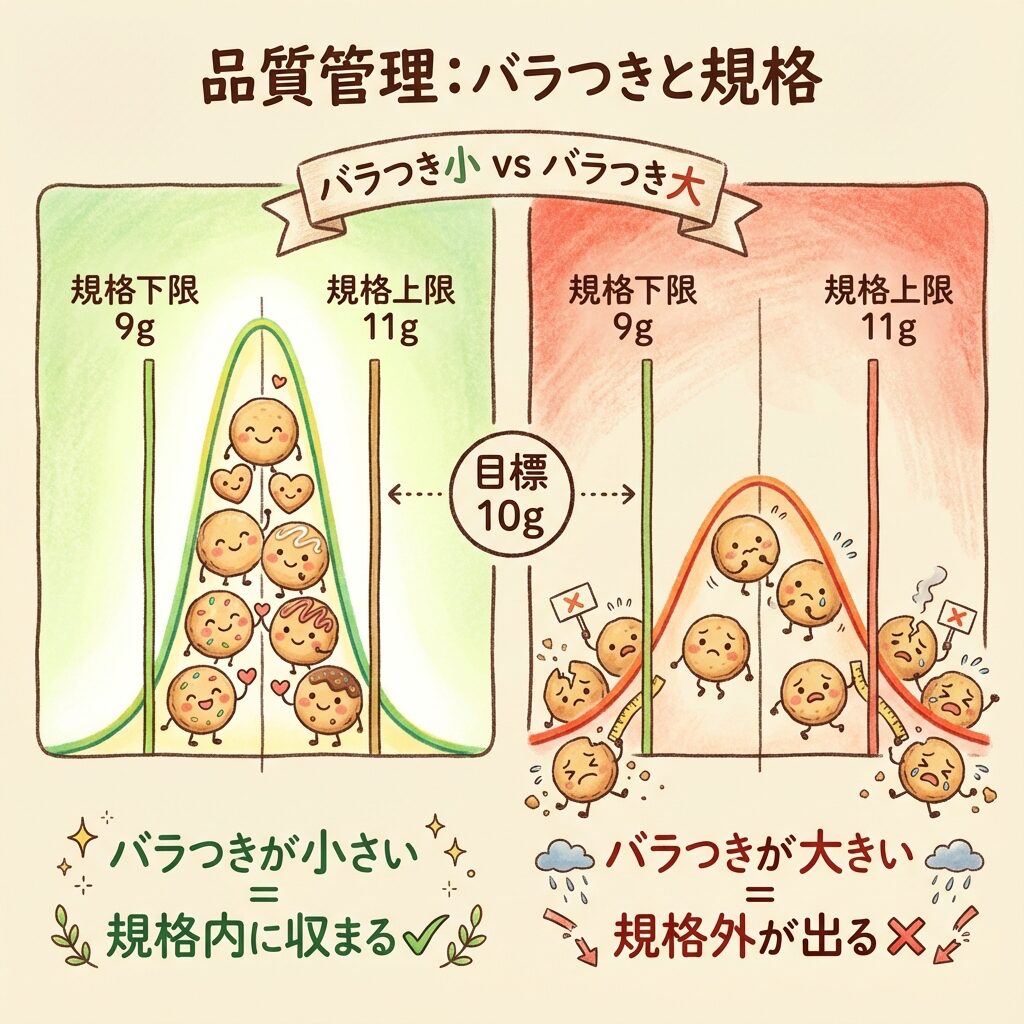
🔹 困ること①:規格を外れる製品が出る
クッキーには「規格」があります。
たとえば、「9g〜11gの範囲に収まること」という基準。
バラつきが小さい工場
→ ほとんどのクッキーが9g〜11gに収まる ✅
バラつきが大きい工場
→ 8gや12gのクッキーが混ざってしまう ❌
→ 規格外品として廃棄 → コスト増!
🔹 困ること②:お客様からのクレーム
バラつきが大きいと、お客様が買うたびに「なんか違う…」と感じます。
🙁「前に買ったときより小さい気がする…」
🙁「1枚だけ焦げてる…」
🙁「品質にムラがあるなぁ…」
→ 信頼を失う → 売上ダウン!
だから、品質管理では「バラつきを小さくする」「バラつきを監視する」ことが超重要なのです。
📊 バラつきを「数値」で表す|平均と標準偏差
「バラつきが大きい」「小さい」と言葉で言っても、あいまいですよね。
だから、数値で表す必要があります。
そこで登場するのが「平均」と「標準偏差」です。
🔹 平均(へいきん)= 真ん中の値
平均は、データの「中心」がどこにあるかを示します。
クッキー5枚の重さ:9.8g, 10.2g, 9.5g, 10.1g, 10.4g
平均 = (9.8 + 10.2 + 9.5 + 10.1 + 10.4) ÷ 5 = 10.0g
平均が10.0gなら、「だいたい目標通りに作れている」ということ。
でも、平均だけではバラつきの大きさは分かりません。
🔹 標準偏差(ひょうじゅんへんさ)= バラつきの大きさ
標準偏差は、データが平均からどれだけ散らばっているかを示します。
記号は「σ(シグマ)」または「s」を使います。
標準偏差が小さい → データが平均の近くに集まっている → バラつき小
標準偏差が大きい → データが平均から離れて散らばっている → バラつき大
🎯 たとえ話:的当てゲーム
的当てゲームで、AさんとBさんが10回ずつ投げました。
Aさん:全部が的の中心付近に集まっている → 標準偏差 小
Bさん:あちこちにバラバラに散らばっている → 標準偏差 大
2人とも平均は「的の中心」かもしれませんが、安定感が全然違いますよね。
平均・分散・標準偏差を詳しく学ぶ →
📈 正規分布と「3σ」の意味
クッキーをたくさん作って、重さを測ってグラフにすると…
不思議なことに、いつも「山」のような形になります。
これが「正規分布(せいきぶんぷ)」です。
別名「ベルカーブ」とも呼ばれます。鐘(ベル)の形に似ているからです。
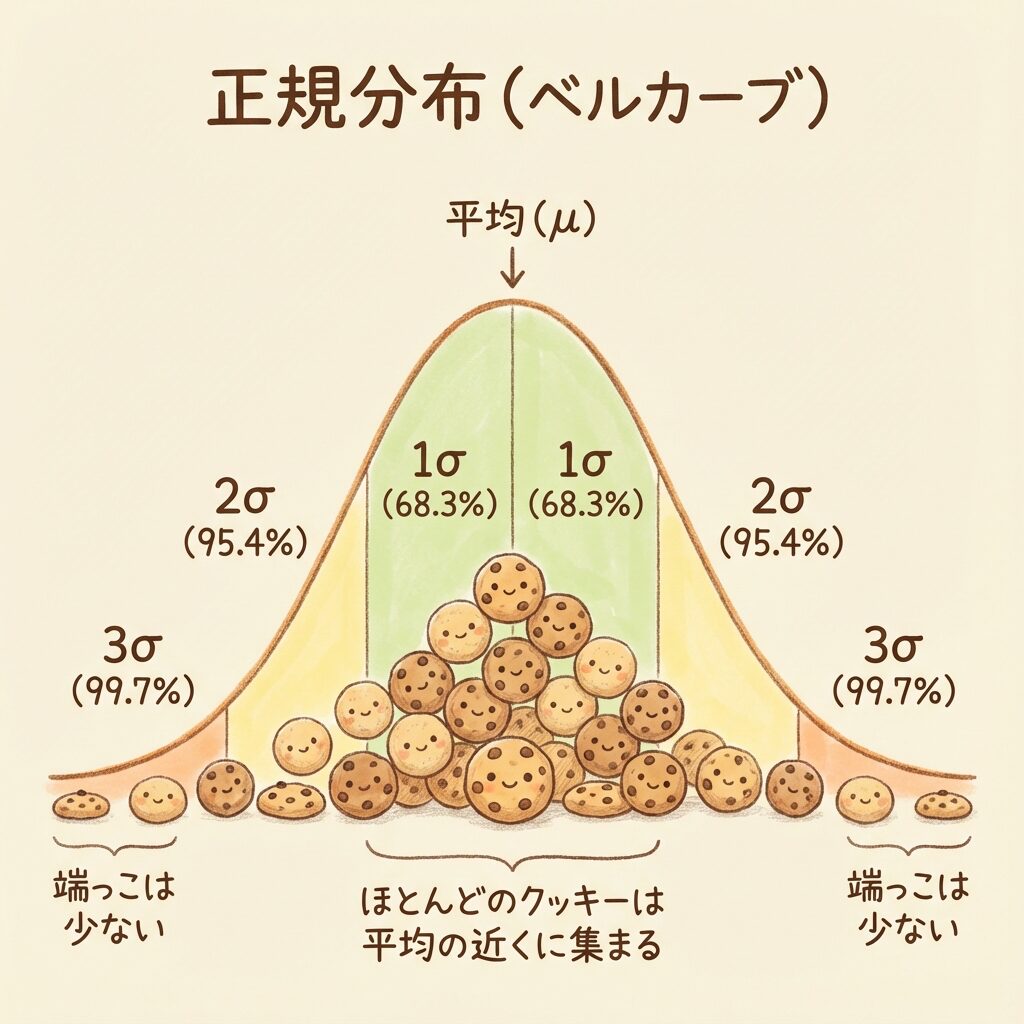
🔹 正規分布の特徴
- 中心(平均)が一番高く、左右対称の山型
- 平均の近くにデータが集まり、端にいくほど少なくなる
- 自然界や工業製品のバラつきは、だいたい正規分布になる
🔹 「3σ(スリーシグマ)」の魔法
正規分布には、とても便利な法則があります。
「平均から±3σの範囲に、99.7%のデータが収まる」という法則です。
| 範囲 | 収まるデータの割合 | イメージ |
|---|---|---|
| 平均 ± 1σ | 約68.3% | 約3分の2 |
| 平均 ± 2σ | 約95.4% | ほとんど |
| 平均 ± 3σ | 約99.7% | ほぼ全部 |
平均 = 10g、標準偏差 = 0.3g のとき
平均 ± 3σ = 10 ± 0.9 = 9.1g 〜 10.9g
つまり、99.7%のクッキーが9.1g〜10.9gに収まるということ。
1000枚作っても、この範囲を外れるのは3枚だけ!
正規分布をもっと詳しく学ぶ →
🔗 管理図・工程能力指数との「つながり」
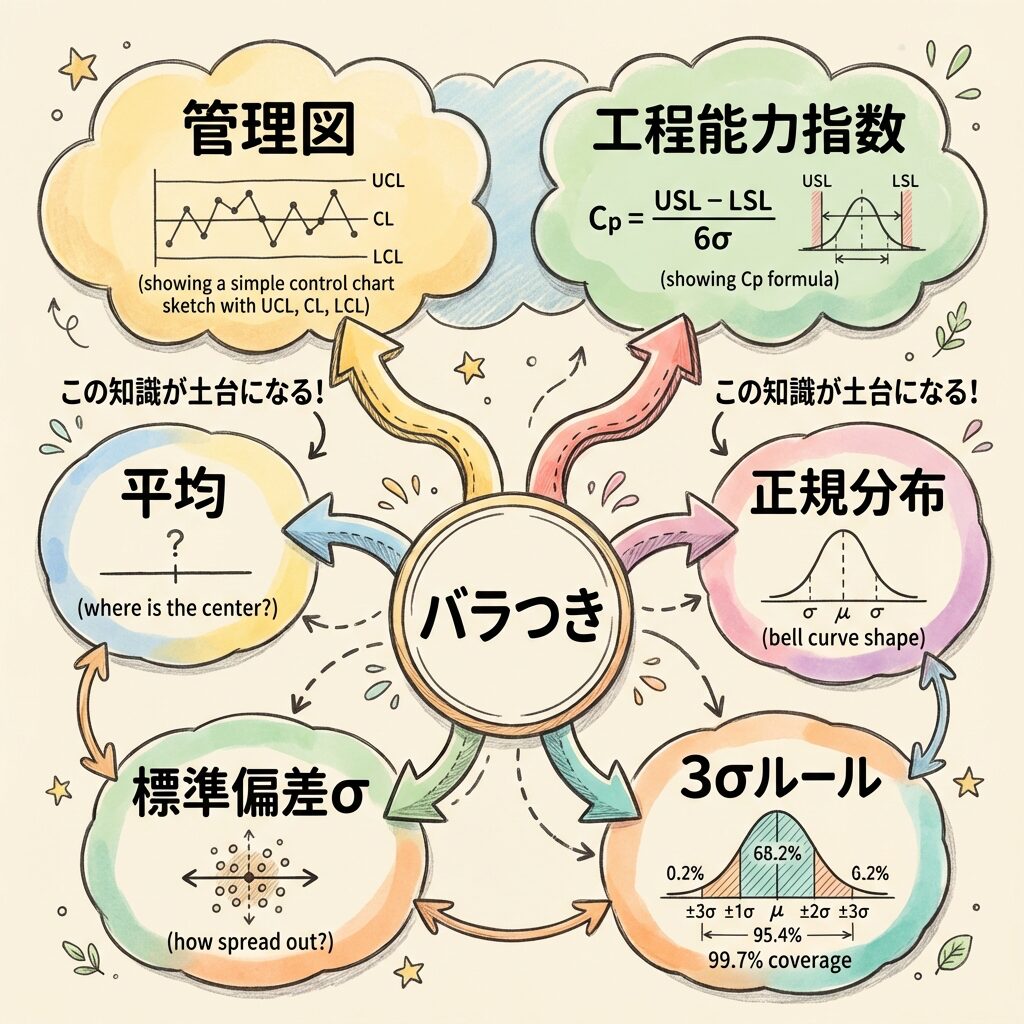
ここまでで学んだ「バラつき」「平均」「標準偏差」「正規分布」「3σ」。
これらは、管理図と工程能力指数の土台になります。
🔹 管理図との関係
管理図の上方管理限界線(UCL)と下方管理限界線(LCL)は、
実は「平均 ± 3σ」の考え方で計算されています。
UCL(上方管理限界) ≒ 平均 + 3σ
CL(中心線) = 平均
LCL(下方管理限界) ≒ 平均 − 3σ
→ 99.7%のデータはUCLとLCLの間に収まるはず
→ もし超えたら「異常」の可能性!
🔹 工程能力指数との関係
工程能力指数(Cp・Cpk)は、
「規格の幅」と「6σ(バラつきの幅)」を比較するものです。
Cp = 規格の幅 ÷ 6σ
→ Cpが大きい = 規格に対してバラつきが小さい = 優秀な工程 ✅
→ Cpが小さい = 規格に対してバラつきが大きい = 改善が必要 ❌
📝 まとめ|バラつきの基礎はこれでOK!
この記事では、管理図を学ぶ前に知っておくべき「バラつき」の基礎を解説しました。
✅ この記事のポイント
| バラつき | 同じはずなのに、違いが出ること |
| なぜ問題? | 規格外品が出る、クレームにつながる |
| 平均 | データの「中心」がどこか |
| 標準偏差(σ) | データがどれだけ散らばっているか |
| 正規分布 | バラつきは山型(ベルカーブ)になる |
| 3σルール | 平均±3σに99.7%が収まる |
これらの知識があれば、管理図の「UCL・CL・LCL」や、工程能力指数の「Cp・Cpk」が何を計算しているのかがスッと理解できるようになります。
準備は整いました!
次は、いよいよ管理図の本格的な学習に進みましょう。
🔗 このシリーズの記事一覧
📍 今ここ
【超入門】品質管理の"バラつき"って何?
📗 管理図の基礎
📘 管理図の計算方法
📙 工程能力指数
管理図と工程能力指数の完全ロードマップ →
