※本記事にはプロモーション（広告）が含まれています。
- t分布がどんな形をしているかイメージでわかる
- なぜデータが少ないと判定基準が厳しくなるのか理解できる
- 自由度とt分布の形の関係がスッキリわかる
- t分布が正規分布に近づいていく仕組みがわかる
この記事を読む前に
この記事はt検定（一標本）の続きです。
t分布の基礎を先に学びたい方は、こちらの記事がおすすめです。
前回、t検定の計算方法を学びましたね。
その中で、こんな疑問を持ちませんでしたか？
「なんでZ検定は1.96なのに、t検定は2.262とか違う値なの？」
「自由度が変わると、なんで判定基準が変わるの？」
「データが少ないと厳しくなるって、どういう意味？」
この疑問の答えは、t分布の「形」を見れば一発でわかります。
今回は、t分布と自由度の関係を、イメージで徹底的に理解していきましょう。
t分布のイメージ｜「自信がない分、広く構える」
まず、t分布がどんな形をしているか、イメージで掴みましょう。
正規分布とt分布を並べてみよう
正規分布とt分布、どちらも「釣鐘型（ベルカーブ）」の形をしています。
でも、よく見ると違いがあります。
t分布の特徴は、「裾野が広い」ことです。
これを別の言い方をすると、「極端な値が出やすい」ということになります。
たとえ話で理解しよう｜「慎重なアーチャー」
t分布と正規分布の違いを、弓矢の的当てでたとえてみましょう。
「的当てゲーム」でたとえると…
神様（正規分布・Z検定）
「的の位置を完璧に知っている」
→ 自信を持って的の中心を狙える
→ 矢は中心付近に集中する
人間（t分布・t検定）
「的の位置をだいたいしか知らない」
→ ちょっと不安なので、広めに狙う
→ 矢は中心からズレやすい（裾野が広い）
t分布の「裾野が広い」とは、「不確実さを反映している」ということなんです。
自由度とは？｜「自信の度合い」を表す数字
t検定では、自由度という数字が登場しますね。
一標本t検定の場合、自由度 = n − 1（データ数 − 1）です。
この「自由度」は、t分布の「形」を決めるパラメータです。
自由度が変わると、t分布の形はどう変わる？
ここが今日の最重要ポイントです。
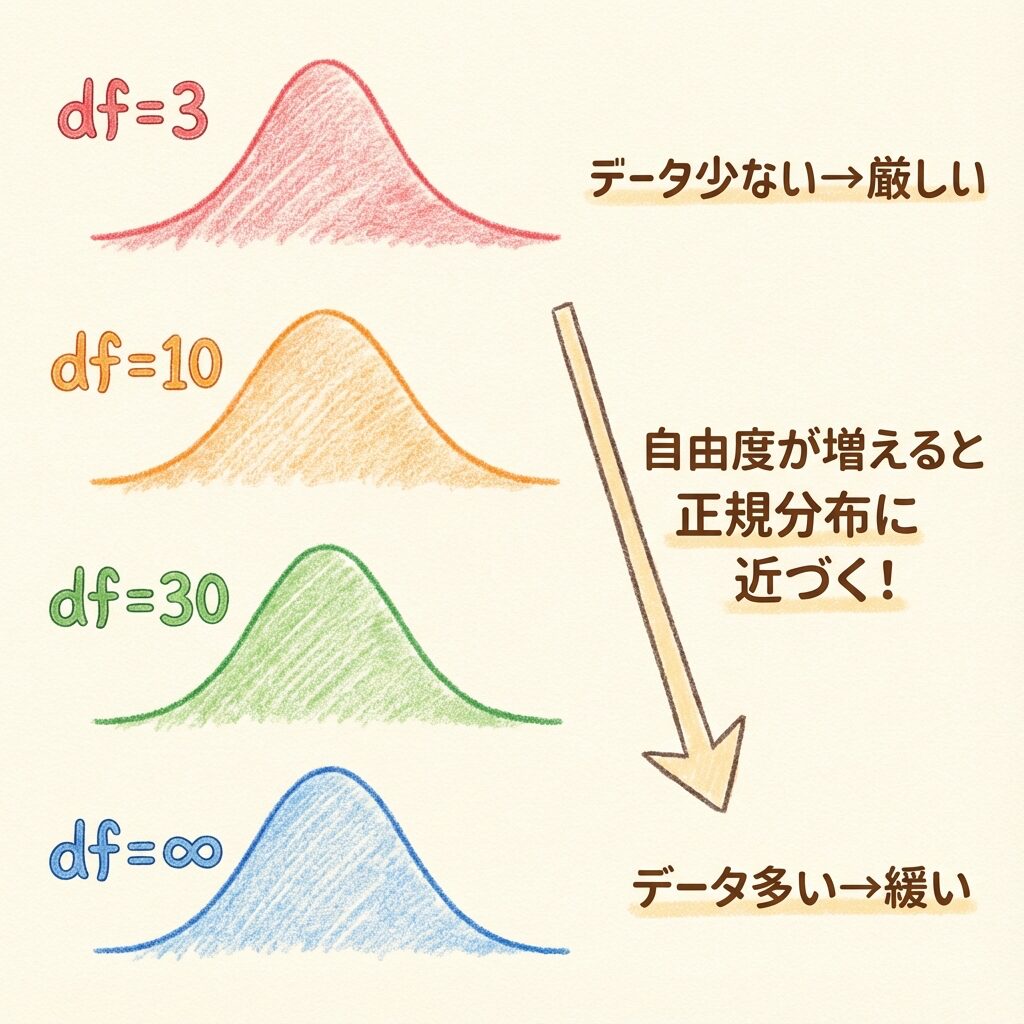
自由度が変わると、t分布の形はこう変わる！
自由度が小さい（データが少ない）
裾野がとても広い → 極端な値が出やすい → 判定基準がかなり厳しい
自由度が中くらい
裾野がやや広い → まだ正規分布より不確実 → 判定基準がやや厳しい
自由度が大きい（データが多い）
裾野が狭くなる → 正規分布に近づく → 判定基準が緩くなる
自由度が無限大
正規分布と一致！ → 判定基準は1.96（Z検定と同じ）
自由度が大きくなる → t分布は正規分布に近づく
つまり、データ数が増えれば増えるほど、
t検定はZ検定に近づいていくのです。
たとえ話で理解しよう｜「経験を積んだ職人」
「寿司職人」でたとえると…
新人職人（自由度が小さい＝データが少ない）
「まだ3回しか握ってない…」
→ 自分の腕に自信がない
→ お客さんも「この人大丈夫？」と厳しい目で見る
ベテラン職人（自由度が大きい＝データが多い）
「10000回握ってきた」
→ 自分の腕に自信がある
→ お客さんも「この人なら安心」と信頼する
経験（データ）が少ないうちは、「たまたまうまくいった」可能性を疑われる。
だから、より厳しい基準で判定される必要があるのです。
臨界値の変化を数字で確認しよう
「裾野が広い」「判定基準が厳しい」という話を、実際の数字で確認しましょう。
有意水準α = 5%（両側検定）のときの臨界値を見てください。
| 自由度 (df = n-1) |
データ数 (n) |
臨界値 (α=5%, 両側) |
判定の厳しさ |
|---|---|---|---|
| 3 | 4 | 3.182 | かなり厳しい |
| 5 | 6 | 2.571 | 厳しい |
| 9 | 10 | 2.262 | やや厳しい |
| 19 | 20 | 2.093 | 普通 |
| 29 | 30 | 2.045 | ほぼ正規分布 |
| ∞ | ∞ | 1.960 | 正規分布と一致 |
- 自由度3（データ4個）では、臨界値が3.182（かなり厳しい！）
- 自由度が増えると、臨界値はだんだん小さくなる
- 自由度∞では、臨界値が1.960（Z検定と同じ！）
- 一般的に、自由度30以上なら正規分布とほぼ同じとみなせる
図でイメージしよう｜「ゴールラインの位置」
臨界値の違いを、「ゴールラインの位置」でたとえてみましょう。
「有意差を出す」＝「ゴールラインを超える」
0 ─────────────────────── │ 3.182 (df=3)
0 ───────────────────── │ 2.571 (df=5)
0 ─────────────────── │ 2.262 (df=9)
0 ───────────────── │ 1.960 (df=∞)
データが少ないと、ゴールラインが遠くにある（超えるのが大変）
データが多いと、ゴールラインが近くにある（超えやすい）
なぜ「厳しく」する必要があるのか？
「データが少ないから厳しくする」というのは、感覚的には理解できますよね。
でも、なぜ統計学的にそうなるのか、もう少し深掘りしてみましょう。
理由①：標本標準偏差の「ブレ」が大きい
t検定では、母分散の代わりに標本標準偏差（s）を使います。
でも、この「s」はサンプルから計算した推定値です。
データが少ない場合
サンプルが少ない
→ sの計算が不安定
→ 「たまたま」の影響を受けやすい
データが多い場合
○
サンプルが多い
→ sの計算が安定
→ 真の値に近づく
データが少ないと、標本標準偏差sが真の値からズレやすいんです。
そのズレを考慮して、判定基準を厳しくしておく必要があるのです。
詳しくは不偏分散の記事で解説しています。
品質保証の現場では、試作品の評価や破壊試験のように「サンプルが3個や5個しか取れない」場面が日常的にあります。本記事のとおり自由度が小さいほど臨界値が大きくなる（判定が厳しくなる）ので、少サンプルの試験では「差があるはずなのに有意にならない」ことが頻発します。これは検出力が低いせいで、t検定が正しく機能している証拠でもあります。ここで「有意差なし＝差がない」と結論づけてしまうのが一番多いミスです。正しくは「このサンプル数では差を検出できなかった」であって、差がないことの証明にはなりません。
実務で効いてくるのが、本記事の「自由度30が境界」という目安です。30個もデータが取れればt検定はほぼZ検定と同じになり、サンプル数の少なさを気にする必要がなくなります。逆に言えば、評価計画を立てる段階で「何個測れば狙った差を有意にできるか」をサンプルサイズ設計で先に決めておくと、試験後に「データが足りなくて判定できなかった」という手戻りを防げます。測ってから考えるのではなく、測る前にnを決めるのが現場の鉄則です。
もう一つの落とし穴が、少サンプルでの正規性の前提です。データが多ければ多少分布が崩れても問題になりにくいのですが、n=4や5では1個の外れ値が平均も標準偏差も大きく動かし、t検定の結果を簡単にひっくり返します。少サンプルのときほど、検定にかける前に必ず生データと外れ値を目で確認するクセが重要になります。
理由②：「たまたま」のリスクを抑える
データが少ないと、「たまたま」極端な結果が出やすいんです。
「コイン投げ」でたとえると…
コインを4回投げた場合
「4回中4回とも表が出た！」 → 表の確率100%？
いやいや、たまたまでしょ…と疑う余地がある
コインを100回投げた場合
「100回中52回表が出た」 → 表の確率約50%
これなら信頼できそうと思える
データが少ない状態で「有意差あり！」と判定すると、第1種の過誤（あわてんぼうのミス）のリスクが高まります。
そのリスクを抑えるために、判定基準を厳しくするのです。
実務での目安｜「自由度30」がひとつの境界線
統計学の世界では、こんな目安があります。
実務での目安
- 自由度 ≤ 30（データ31個以下）：t分布を使う
- 自由度 ＞ 30（データ32個以上）：正規分布で近似してもOK
※ 厳密には、常にt分布を使う方が正確です。
Excelなどの統計ソフトは自動的にt分布で計算してくれます。
t分布誕生の物語 〜ビール会社の品質管理〜
ここで、t分布がどのように生まれたのか、その歴史を見てみましょう。
1908年、アイルランドのダブリン
ギネスビールで有名なギネス社で働く統計学者、ウィリアム・シーリー・ゴセットさんには、大きな悩みがありました。
ゴセットさんの悩み
「ビールの品質をチェックしたいけど、毎日何百本も検査するわけにはいかない…。せいぜい10〜20本が限界だ」
当時、品質管理といえば正規分布を使うのが常識でした。でも、正規分布は「データがたくさんある」ことが前提。少ないデータで使うと、信頼性に問題が…。
画期的な発見
そこでゴセットさんは考えました。
「少ないデータでも使える、新しい分布を作れないかな？」
研究の結果、ついに「データ数が少ない時の不確かさを考慮した分布」を発見！これが現在のt分布です。
なぜ「Student」なのか？
でも、ギネス社は社員の研究成果を外部発表することを禁止していました。
そこでゴセットさんは、「Student（学生）」という偽名で論文を発表したのです！
だから今でも…
t分布 → 「Student's t-distribution」
t検定 → 「Student's t-test」と呼ばれる
普段飲んでいるビールの品質管理から生まれた分布が、今では世界中で使われているなんて、素敵な話ですよね！
t分布が活躍する場面
t分布は、実は私たちの身近なところで大活躍しています。
場面①：製品の品質管理
「新製品の試作品が10個しかない。この品質は基準を満たしている？」
→ t分布で信頼区間を計算し、品質保証ができる。
場面②：医薬品の効果測定
「治験参加者が20人だけ。この薬は効果がある？」
→ t検定で「効果あり」かどうかを統計的に判断できる。
場面③：マーケティング効果測定
「A/Bテストの各グループが25人ずつ。どっちの広告が効果的？」
→ t検定で2つのグループを比較できる。
場面④：教育効果の測定
「新しい教材を試したクラスが18人。成績は上がった？」
→ 対応のあるt検定で「ビフォー・アフター」を比較できる。
まとめ｜t分布は「不確実さの反映」
この記事のまとめ
- t分布は正規分布より裾野が広い（極端な値が出やすい形）
- 自由度が小さいほど裾野が広く、判定基準が厳しくなる
- 自由度が大きくなると、t分布は正規分布に近づく
- 自由度∞で正規分布と一致（臨界値1.96）
- これは「データが少ない＝不確実」を数学的に反映している
覚え方のコツ
自由度が小さい ＝ 自信がない ＝ 厳しく判定
新人は厳しく評価される、ベテランは信頼されるのと同じ！
t分布と自由度の関係を理解したら、次は「2つのグループを比較するt検定」を学びましょう。
「A組とB組の平均に差はあるか？」のような、2標本の比較ができるようになります。
ここまで読んでくださった方へ
「なぜ自由度で判定基準が変わるのか？」
この疑問が、イメージで理解できましたね！
データが少ない＝不確実＝厳しく判定
この感覚を身につけておくと、
t検定の結果を正しく解釈できるようになります！
製造業の品質保証の現場で、試作評価や破壊試験など「サンプルが数個しか取れない」状況でt検定を実際に使ってきました。少サンプルだと有意差が出にくいこと、それを「差がない」と取り違えないこと、測る前にサンプル数を決めることといった、現場でつまずきやすい点を自分の経験を踏まえて解説しています。
「t分布と自由度」の土台になる統計学を、本でじっくり学び直したいときに向いています。統計学を独学で学べるように書かれた入門書です（ダイヤモンド社、小島寛之 著）。
QC検定2級の受験を考えているなら、過去問で出題のされ方を確かめておきましょう。QC検定2級の過去問題を、解説つきで学べる問題集です（日本規格協会、2026年版）。
「t分布と自由度」の土台になる統計学を、検定まで含めて1冊で学びたいときに向いています。検定から多変量解析・実験計画法・ベイズ統計学までを扱う、統計学の入門書です（オーム社、栗原伸一 著、第2版）。
メーカーで電気設計と品質保証に携わってきた経験をもとに執筆しています。むずかしい専門用語をできるだけ使わず、はじめて学ぶ人がつまずかないように、図とたとえで説明することを大切にしています。
次に読むべき記事
この記事の内容がわかったら、検定と推定の次のテーマに進みましょう。続けて読むと、現場でそのまま使える知識になります。
テーマ別に、もっと深く学ぶ
気になるところから読んでも大丈夫です。どの記事も、はじめて学ぶ人向けにやさしく書いています。
