- ハートレーの検定が「何のための検定か」がイメージでわかる
- コクランの検定との違いがスッキリ理解できる
- 計算式の意味を「クラスの体力差」で直感的に理解できる
- Fmax(エフマックス)という統計量の意味がわかる
前回、「コクランの検定」を学びましたね。
コクランは「最大のバラつきが、全体の中でどれくらいの割合を占めるか」を調べる検定でした。
今回紹介する「ハートレーの検定(Hartley's test)」は、もっとシンプルです。
ハートレーの検定は、
「一番バラついている群」と「一番揃っている群」の差
を調べる検定です。
計算式は超シンプル。最大の分散 ÷ 最小の分散、これだけ!
目次
ハートレーの検定のイメージ|「両端の差」を見る
ハートレーの検定を理解するために、「クラスの体力テスト」をイメージしてみましょう。
3クラスの体力テスト結果
A組・B組・C組で体力テストを行いました。
各クラスの「点数のバラつき(分散)」を見てみると…
10
バラつき:小
25
バラつき:中
50
バラつき:大
ハートレーが見るのは「両端」
ハートレーの検定は、「最もバラついているクラス」と「最も揃っているクラス」だけに注目します。
50
(C組)
10
(A組)
5.0
「一番バラついているクラスは、一番揃っているクラスの5倍もバラついている!」
「この差は許容範囲? それとも大きすぎ?」
この「何倍か」を調べるのがハートレーの検定です。

コクランとハートレーの違い|「割合」vs「倍率」
コクランの検定とハートレーの検定、どちらも「等分散性」を調べる検定ですが、見ているポイントが違います。
比較表で整理しよう
| コクランの検定 | ハートレーの検定 | |
|---|---|---|
| 計算式 | Vmax / ΣVi (最大÷合計) |
Vmax / Vmin (最大÷最小) |
| 見ているもの | 割合 「全体の何%?」 |
倍率 「何倍違う?」 |
| イメージ | 🍰 ケーキの取り分 「1人だけ取りすぎ?」 |
📏 身長差 「一番と最下位の差は?」 |
| 統計量の名前 | G | Fmax |
| 計算の簡単さ | 合計を計算する必要あり | 超簡単! 割り算1回だけ |
例え話で理解しよう
「3人でケーキを分けて、
1人だけ70%も取ってない?」
→ 全体に対する「割合」を見る
「クラスで一番背が高い子と低い子、
何倍も違わない?」
→ 両端の「倍率」を見る
実務ではどちらを使っても大きな差はありません。
ただし、ハートレーの方が計算が簡単なので、
手計算が必要な場面(試験など)では重宝します。
QC検定では両方とも出題されるので、両方覚えておきましょう!

ハートレーの検定の計算式|最大÷最小
計算式は統計学の中でもトップクラスにシンプルです。
ハートレーの統計量 Fmax
Vmin:各群の分散の中で最小のもの
これだけです。割り算1回で終わり!
Fmaxの意味を直感的に理解する
Fmaxは「最大のバラつきが、最小のバラつきの何倍か」を表しています。
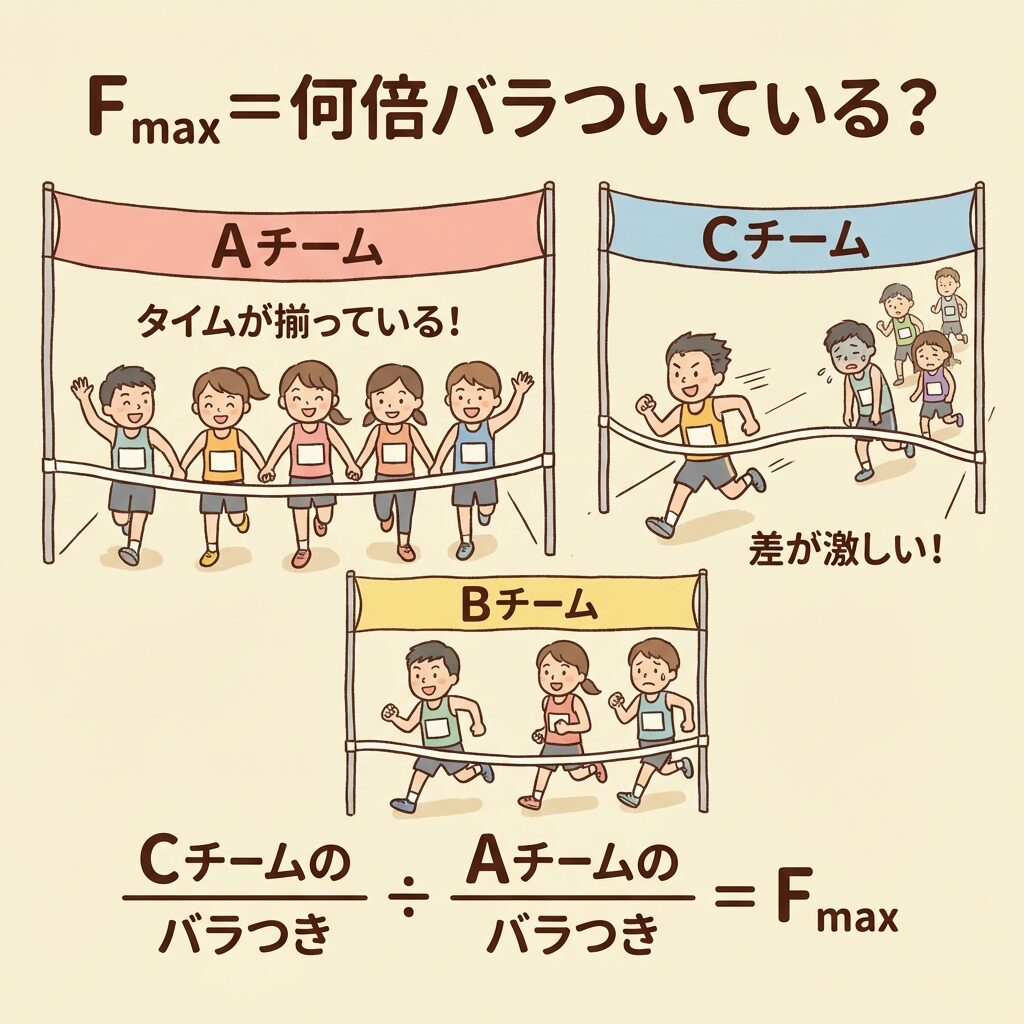
3チームでマラソン大会をしました。
Aチーム:全員が近いタイムでゴール(バラつき小)
Bチーム:まあまあバラバラ(バラつき中)
Cチーム:速い人と遅い人の差が激しい(バラつき大)
Fmax = Cチームのバラつき ÷ Aチームのバラつき
もしFmaxが10倍なら…
「Cチームの実力差は、Aチームの10倍もバラバラってこと!?
これはさすがに差がありすぎでは?」
Fmax ≈ 1:最大と最小がほぼ同じ → 等分散(理想的!)
Fmax = 3:最大は最小の3倍 → まだ許容範囲かも?
Fmax = 10:最大は最小の10倍 → 等分散とは言えない!
具体例で計算してみよう
実際にデータを使って計算してみましょう。
ケーススタディ:3台の機械の精度比較
3台の機械(A・B・C)で製品を各5回ずつ作り、寸法のバラつき(分散)を計算した。
| 機械 | 分散 V | 備考 |
|---|---|---|
| A | 4 | ← 最小 |
| B | 9 | |
| C | 16 | ← 最大 |
→ 最大の分散は、最小の分散の4倍!
計算はこれで完了。あとは臨界値と比較するだけです。
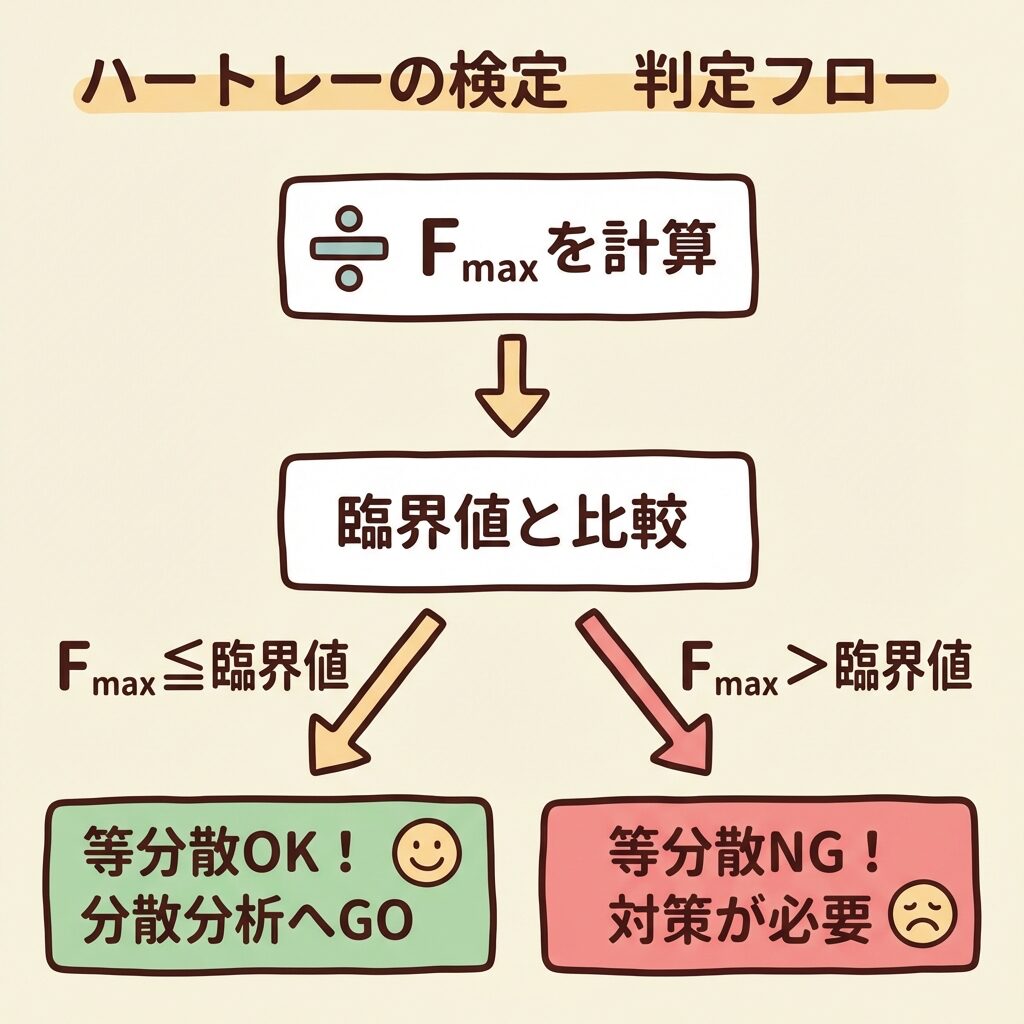
判定方法|Fmaxを臨界値と比較する
計算したFmaxを、ハートレーの臨界値表と比較して判定します。
判定ルール
(帰無仮説を棄却しない)
→ 分散分析に進んでOK!
(帰無仮説を棄却)
→ そのまま分散分析するのは危険!
ハートレーの臨界値表(抜粋)
有意水準 α = 0.05 の場合の臨界値を示します。
| 群の数 k |
各群の自由度 φ = n - 1 | ||||
|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 10 | |
| 2 | 39.0 | 15.4 | 9.60 | 7.15 | 4.85 |
| 3 | 87.5 | 27.8 | 15.5 | 10.8 | 6.34 |
| 4 | 142 | 39.2 | 20.6 | 13.7 | 7.11 |
| 5 | 202 | 50.7 | 25.2 | 16.3 | 7.80 |
| 6 | 266 | 62.0 | 29.5 | 18.7 | 8.38 |
k:比較する群の数(機械の台数など)
φ(ファイ):各群の自由度 = n - 1(データ数 - 1)
⚠️ コクランは「データ数 n」を使いますが、
ハートレーは「自由度 φ = n - 1」を使います!
例:3台の機械で、各5回ずつ測定した場合
→ k=3, φ=5-1=4 の交点 = 15.5 が臨界値
具体例で判定してみよう
先ほどの計算例で、実際に判定してみましょう。
ケーススタディの続き
- 機械の台数:k = 3
- 各機械のデータ数:n = 5 → 自由度 φ = 4
- 計算したFmax:4.0
- 有意水準:α = 0.05
表から k=3, φ=4 の値を探すと…
臨界値 = 15.5
Fmaxが臨界値以下なので、
等分散とみなせる
→ 分散分析(ANOVA)に進んでOK!
「C機のバラつき(16)はA機(4)の4倍だけど、
3群で自由度4なら、15.5倍までは許容範囲。
4倍程度なら誤差の範囲内だね」
という判断になります。
コクランとハートレー、どっちを使う?
両方とも等分散性を調べる検定ですが、使い分けの目安があります。
使い分けガイド
| 状況 | コクラン | ハートレー |
|---|---|---|
| データ数が等しい場合 | ○ 使える | ○ 使える |
| 計算の簡単さ | 合計を計算 | 割り算1回 |
| 「1つだけ突出」を見つけたい | ◎ 得意 | ○ できる |
| 「両端の差」を見たい | △ 苦手 | ◎ 得意 |
| 試験での出題頻度 | 高い | 高い |
正直なところ、どちらを使っても結論はほぼ同じになります。
ハートレー:計算が超簡単 → 手計算向き
コクラン:「突出」を見つけやすい → 問題児探し向き
試験では問題文で指定されることが多いので、
両方の計算方法と表の見方を覚えておきましょう!

まとめ|ハートレーは「両端の差」を見る
「最大のバラつき」と「最小のバラつき」の差(倍率)を調べる
→ 「何倍違うか」で等分散性を判定
Fmax = Vmax / Vmin(最大÷最小)
→ 割り算1回で終わり!
コクラン:最大 ÷ 合計(割合を見る)
ハートレー:最大 ÷ 最小(倍率を見る)
ハートレーは自由度 φ = n - 1 を使う
(コクランはデータ数 n を使う)
ハートレー = 「ハート(心)」の両端=両極端を比べる
最大と最小、両端だけを見て「何倍違う?」を調べる検定です。
次に学ぶべきこと
コクランとハートレーで「等分散性OK」と確認できたら、いよいよ分散分析(ANOVA)に進みましょう。
分散分析では、「3群以上の平均に差があるか?」を判定します。
💪 ここまで読んでくださった方へ
「ハートレーの検定」、
「両端の差を見る」というイメージで覚えられましたね!
計算は超シンプル、最大÷最小だけ。
コクランと合わせて、等分散性検定はこれで完璧です。
分散分析の「前座」として、
しっかり使いこなせるようになりましょう!
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


