数量化理論とは？｜Ⅰ類・Ⅱ類・Ⅲ類・Ⅳ類の違いをイメージでマスター

※本記事にはプロモーション（広告）が含まれています。

こんな疑問、ありませんか？

数量化理論って何？なぜ「数量化」というの？
Ⅰ類・Ⅱ類・Ⅲ類・Ⅳ類の違いがわからない…
どんな場面で使うの？回帰分析や主成分分析と何が違う？

○ この記事でスッキリ解決！
「アンケート調査」「顧客分類」など身近な例えで、数量化理論の全体像を完全マスターできます！

この記事の結論（先に知っておこう！）

数量化理論は「文字データ（カテゴリデータ）を数値に変換して分析する」ための手法です。日本の統計学者・林知己夫が開発した「Made in Japan」の分析手法。Ⅰ類〜Ⅳ類の4種類があり、目的変数の有無とデータの種類で使い分けます！

数量化理論って何？｜一言でいうと

数量化理論を一言で説明すると…

「男・女」「好き・嫌い」などの
文字データを数値に変換して分析する手法

なぜ「数量化」が必要なの？

統計分析の多くは「数値データ」を前提としています。

数値データ

身長：170cm
体重：65kg
年収：500万円

→ そのまま分析できる！

カテゴリデータ

性別：男・女
血液型：A・B・O・AB
満足度：満足・普通・不満

→ そのままでは分析できない…

アンケート調査や顧客データには、「男・女」「好き・嫌い」「購入する・しない」などのカテゴリデータがたくさん含まれています。

これらを数値に変換して分析できるようにしたのが、数量化理論です！

開発者は日本人！

数量化理論は、日本の統計学者林知己夫（はやしちきお）が1950年代に開発しました。海外では「Hayashi's Quantification Methods」として知られています。日本発の統計手法として、世界的に認められています。

4つの数量化理論｜全体マップ

数量化理論にはⅠ類・Ⅱ類・Ⅲ類・Ⅳ類の4種類があります。

選び方は2つの軸で決まります。

選び方の2つの軸

軸①：目的変数があるか？

ある：予測・判別したい
（Ⅰ類・Ⅱ類）

ない：構造を知りたい
（Ⅲ類・Ⅳ類）

軸②：目的変数の種類は？

数値：売上、点数など
（Ⅰ類）

カテゴリ：購入する/しない
（Ⅱ類）

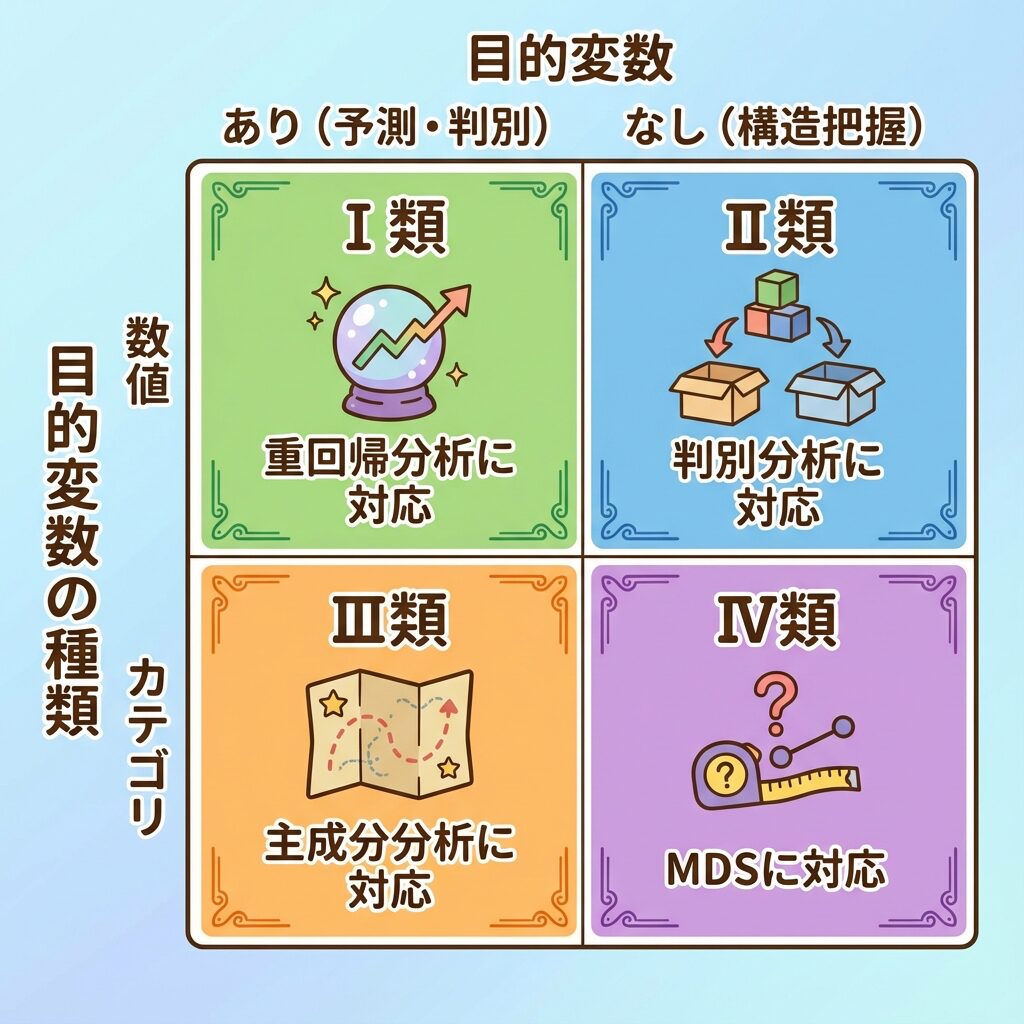
4つの数量化理論早見表

種類	目的変数	何をする？	対応する手法	イメージ
Ⅰ類	数値（あり）	カテゴリで数値を予測	重回帰分析	予測
Ⅱ類	カテゴリ（あり）	カテゴリでグループを判別	判別分析	分類
Ⅲ類	なし	カテゴリ間の関係を可視化	主成分分析コレスポンデンス分析	マップ化
Ⅳ類	なし	サンプル間の類似度を分析	多次元尺度構成法（MDS）	距離

覚え方のコツ：「Ⅰ類とⅡ類は予測・判別（目的変数あり）」「Ⅲ類とⅣ類は構造把握（目的変数なし）」とまず分けて覚えましょう！

数量化Ⅰ類｜カテゴリで数値を予測する

Ⅰ類

カテゴリデータで数値を予測

対応する手法：重回帰分析（説明変数がカテゴリ版）

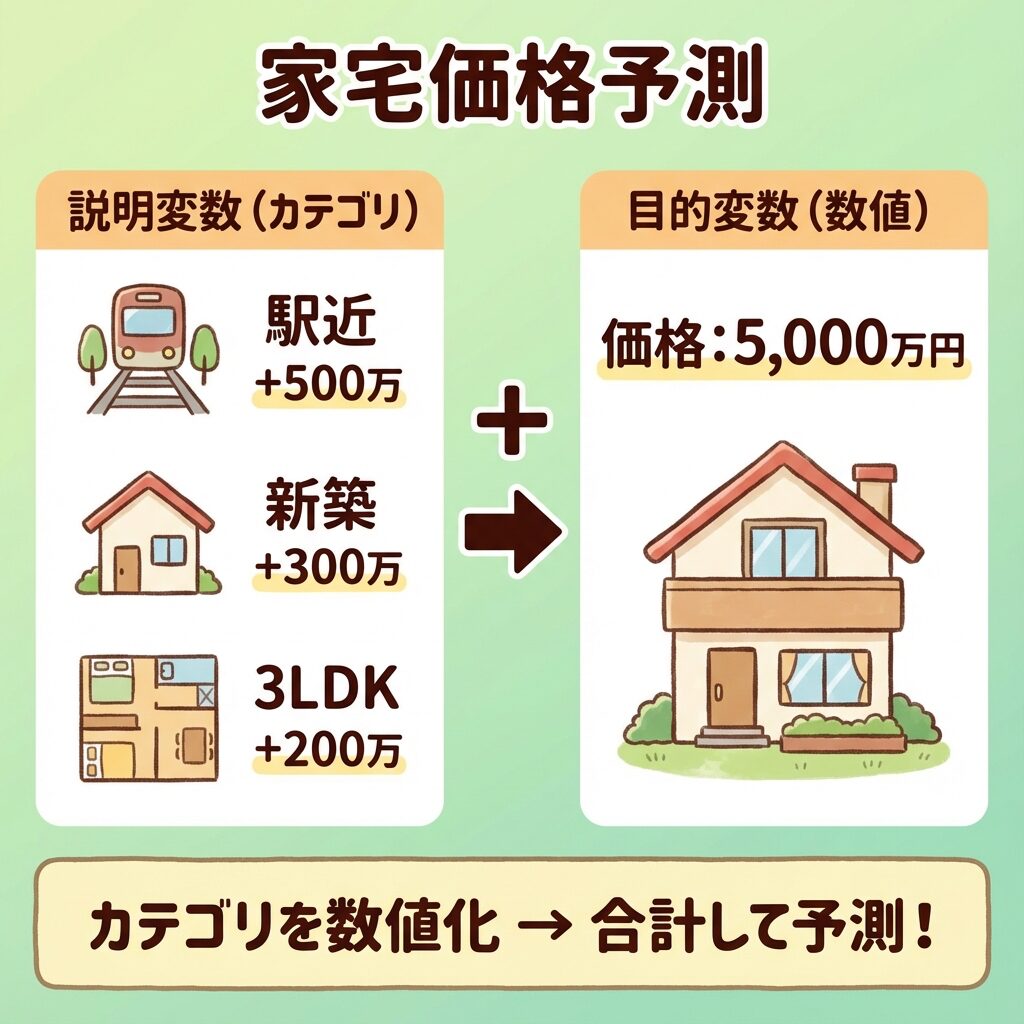
具体例：住宅価格の予測

こんなデータがあるとき…

物件	駅からの距離	築年数	間取り	価格（万円）
A	徒歩5分以内	新築	3LDK	5,000
B	徒歩10分以上	10年以上	2LDK	2,500

「駅からの距離」「築年数」「間取り」などのカテゴリデータから、価格（数値）を予測したい。

こんなときに使うのが数量化Ⅰ類です！

数量化Ⅰ類がやること

「徒歩5分以内」→ +500万円のように、各カテゴリに数値（カテゴリスコア）を割り当てる

各カテゴリのスコアを合計して、価格を予測する

どのカテゴリが価格に影響が大きいかもわかる

数量化Ⅰ類の活用例

住宅価格の予測（立地・築年数・間取りから）
アンケートから顧客満足度を予測
商品の売上を属性から予測
従業員のパフォーマンス予測

数量化Ⅱ類｜カテゴリでグループを判別する

Ⅱ類

カテゴリデータでグループを判別

対応する手法：判別分析（説明変数がカテゴリ版）

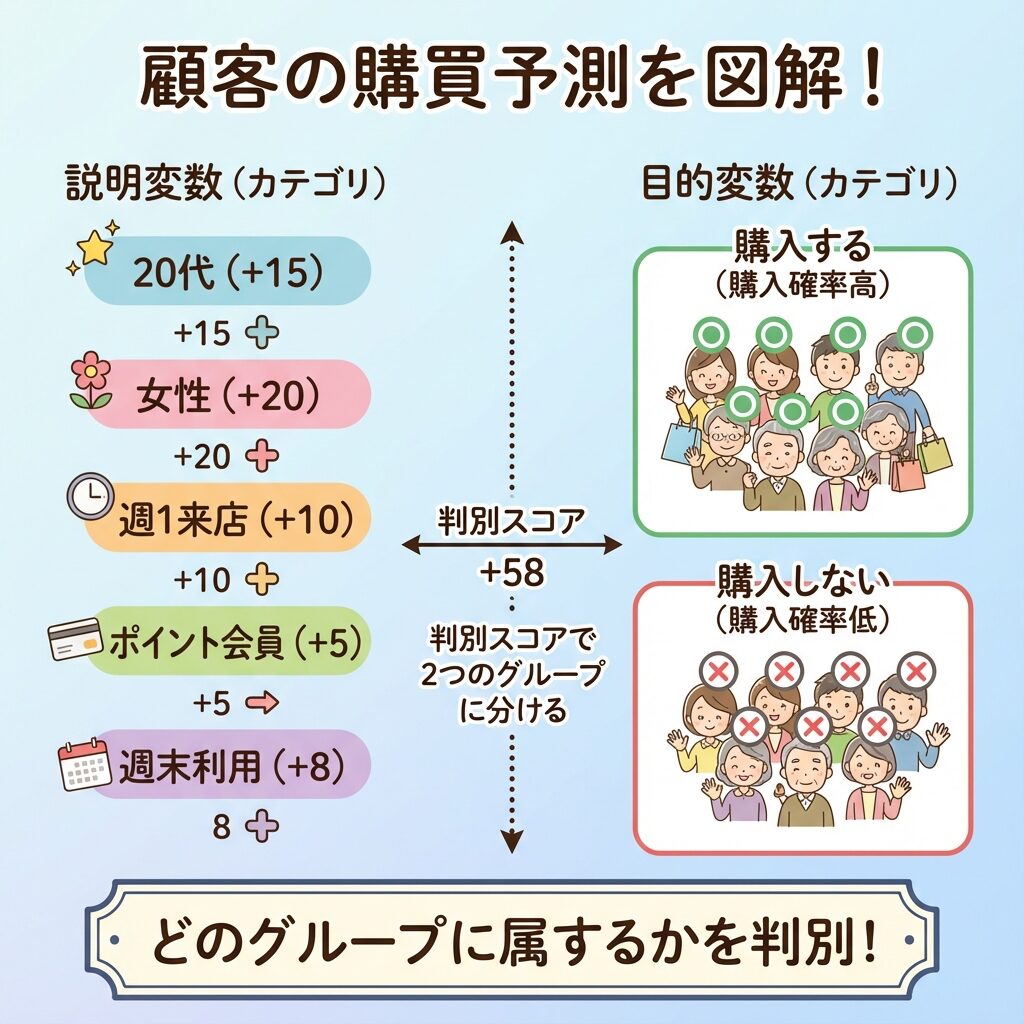
具体例：顧客の購買予測

こんなデータがあるとき…

顧客	年代	性別	来店頻度	購入する？
Aさん	20代	女性	週1以上	購入する
Bさん	50代	男性	月1以下	購入しない

「年代」「性別」「来店頻度」などのカテゴリデータから、「購入する・しない」というグループ（カテゴリ）を判別したい。

こんなときに使うのが数量化Ⅱ類です！

数量化Ⅱ類がやること

各カテゴリにスコアを割り当てる（Ⅰ類と同様）

スコアの合計から「購入する群」と「購入しない群」を最もよく分ける境界線を見つける

新しい顧客がどちらのグループに属するか予測できる

Ⅰ類との違い

Ⅰ類：数値を予測
（例：売上金額、点数）

Ⅱ類：カテゴリを判別
（例：購入する/しない）

活用例

顧客の購買予測
ローン審査の判定
疾患の診断予測
離職者の予測

数量化Ⅲ類｜カテゴリ間の関係を可視化する

Ⅲ類

カテゴリ間の関係を2次元マップで可視化

対応する手法：主成分分析、コレスポンデンス分析（カテゴリ版）

Ⅲ類は目的変数がありません。「予測」ではなく「構造の把握」が目的です。

具体例：テレビ番組と視聴者の関係

こんなデータがあるとき…

視聴者	ドラマA	バラエティB	ニュースC	スポーツD
20代女性	◯	◯	×	×
50代男性	×	×	◯	◯

「どの番組とどの視聴者層が似ているか？」を知りたい。

こんなときに使うのが数量化Ⅲ類です！

数量化Ⅲ類がやること

カテゴリ（番組）とサンプル（視聴者）を同じ2次元マップ上にプロットします。

近くにあるものは「似ている」、遠くにあるものは「似ていない」という関係がわかります。

結果のイメージ

　　　　　↑
　ドラマA ● 　● 20代女性
　バラエティB ●
←─────────────────→
　　　　　　　● ニュースC
　　　　● 50代男性 ● スポーツD
　　　　　↓

近くにあるもの同士は「似ている」！

数量化Ⅲ類の活用例

ブランドイメージと消費者の関係を可視化
アンケート回答パターンの分析
商品と購買者層の対応関係
Webサイトとユーザー属性のマッピング

数量化Ⅳ類｜サンプル間の類似度を分析する

Ⅳ類

類似度データから位置関係を復元する

対応する手法：多次元尺度構成法（MDS：Multidimensional Scaling）

Ⅳ類は他の3つとは少し異なり、「類似度」や「距離」のデータを使います。

具体例：都市間の心理的距離

こんなデータがあるとき…

「東京と大阪は似ている（距離：2）」「東京と札幌はあまり似ていない（距離：5）」のような類似度（距離）データがあるとき…

都市	東京	大阪	札幌	福岡
東京	0	2	5	4
大阪	2	0	6	3

※数字が小さいほど「似ている」

この「距離データ」から、2次元の地図のような配置を復元したい。

こんなときに使うのが数量化Ⅳ類です！

数量化Ⅳ類がやること

「類似度（距離）」のデータを入力とする

距離関係をなるべく再現する2次元座標を計算する

地図のように位置関係を可視化できる

Ⅲ類との違い

Ⅲ類：0/1データ（あり・なし）
→ カテゴリの対応関係

Ⅳ類：距離・類似度データ
→ 位置関係の復元

活用例

ブランドの知覚マップ作成
商品間の類似度分析
消費者の好みの構造分析
音や色の心理的距離の可視化

通常の分析手法との対応関係

数量化理論は、「カテゴリデータ版」の多変量解析と考えることができます。

数量化理論	対応する通常手法	説明変数	目的変数
Ⅰ類	重回帰分析	カテゴリ	数値
Ⅱ類	判別分析	カテゴリ	カテゴリ
Ⅲ類	主成分分析コレスポンデンス分析	カテゴリ	なし
Ⅳ類	多次元尺度構成法（MDS）	類似度データ	なし

現代の実務では…
数量化理論の考え方は、「ダミー変数」を使った回帰分析や、機械学習の「One-Hot Encoding」として広く普及しています。概念を理解しておくと、様々な分析手法の理解が深まります。

まとめ｜数量化理論のポイント

試験で覚えるべきこと

数量化理論とは？

カテゴリデータを数値に変換して分析する、日本発の統計手法

Ⅰ類

カテゴリ → 数値を予測（重回帰分析に対応）

Ⅱ類

カテゴリ → カテゴリを判別（判別分析に対応）

Ⅲ類

カテゴリ間の関係を可視化（主成分分析に対応）

Ⅳ類

類似度データから位置関係を復元（MDSに対応）

選び方のフローチャート

①目的変数はあるか？
　→ ある場合：Ⅰ類 or Ⅱ類
　→ ない場合：Ⅲ類 or Ⅳ類

②目的変数の種類は？（目的変数ありの場合）
　→ 数値：Ⅰ類
　→ カテゴリ：Ⅱ類

③データの種類は？（目的変数なしの場合）
　→ 0/1（あり・なし）：Ⅲ類
　→ 類似度・距離：Ⅳ類

QC検定での出題ポイント

数量化理論はQC検定1級・2級で出題されることがあります。特に以下の点を押さえておきましょう。