- 歪度(わいど)と尖度(せんど)って何?読み方すらわからない…
- 公式が複雑すぎて、何を計算しているのか意味がわからない
- 正規分布のときの値(0と3)を覚えても、なぜその値になるのかわからない
- グラフを見て歪度・尖度を判断する問題が解けない
- 歪度と尖度が「何を測っているのか」をイメージで理解
- 正規分布の基準値(0と3)の意味と覚え方
- グラフを見て一瞬で判断できるようになるコツ
- QC検定・統計検定で出題されるパターンと解き方
「歪度」「尖度」という言葉、なんだか難しそうですよね。
でも実は、これらは「分布の形が正規分布からどれくらいズレているか?」を測る、とてもシンプルな指標なんです。
この記事では、数式をできるだけ使わずに、イメージだけで歪度と尖度を完全理解できるように解説します。最後まで読めば、グラフを見ただけで「歪度はプラス」「尖度は3より大きい」と判断できるようになりますよ。
目次
そもそも歪度・尖度って何のために使うの?
統計学では、データの分布が「正規分布に近いかどうか」を確認することがとても重要です。
なぜなら、多くの統計手法(t検定、回帰分析など)は「データが正規分布に従う」という前提で作られているからです。
では、どうやって「正規分布に近いかどうか」を判断するのでしょうか?
グラフを目で見て「なんとなく釣鐘型だな」と判断するのも一つの方法ですが、それでは客観的・定量的な判断ができません。
そこで登場するのが歪度と尖度という2つの数値です。
| 歪度(わいど) | 分布の「左右の偏り」を数値化 |
| 尖度(せんど) | 分布の「山のとがり具合」を数値化 |
この2つの数値を使えば、「この分布は正規分布からどれくらいズレているか」を客観的な数字で表現できるんです。

歪度(Skewness)とは?─ 左右の偏りを測る
まずは歪度から理解しましょう。
歪度のイメージ:「どっちに裾が長いか?」
歪度は、分布が「左右対称か?」「どちらかに偏っているか?」を測る指標です。
イメージしやすいように、3つのパターンを見てみましょう。
パターン1:左右対称(歪度 = 0)
正規分布のように、真ん中を軸にして左右がピッタリ対称な分布です。
歪度 √b₁ = 0
きれいな釣鐘型
パターン2:右に裾が長い(歪度 > 0:正の歪み)
山のピークが左側にあり、右側に長い裾を引いている分布です。
歪度 √b₁ > 0(プラス)
右に尾を引く(例:年収分布)
パターン3:左に裾が長い(歪度 < 0:負の歪み)
山のピークが右側にあり、左側に長い裾を引いている分布です。
歪度 √b₁ < 0(マイナス)
左に尾を引く(例:寿命分布)
歪度の覚え方:「裾が長い方向」がプラスかマイナスか
「右に裾が長い → 正(プラス)」
「左に裾が長い → 負(マイナス)」
数直線をイメージしてください。右がプラス、左がマイナスですよね。
裾が伸びている方向と符号が一致すると覚えましょう。
身近な例で理解する歪度
| 例 | 分布の形 | 歪度 |
|---|---|---|
| 日本人の年収 | 多くの人は300〜500万円台、一部の高所得者が右に長い裾を作る | 正(+) |
| 製品の寿命 | 多くは長持ち、一部の初期不良品が左に長い裾を作る | 負(−) |
| 身長 | 平均付近に集中し、左右対称に広がる | ≒ 0 |
尖度(Kurtosis)とは?─ 山のとがり具合を測る
次は尖度です。歪度が「左右の偏り」なら、尖度は「上下のとがり具合」を測ります。
尖度のイメージ:「山がとがっているか?平べったいか?」
尖度は、分布の山が「尖っているか」「平べったいか」を測る指標です。
ただし、ここで超重要なポイントがあります。
正規分布の尖度 = 3
この「3」が基準値です。必ず覚えてください!
つまり、尖度は「3より大きいか小さいか」で判断します。
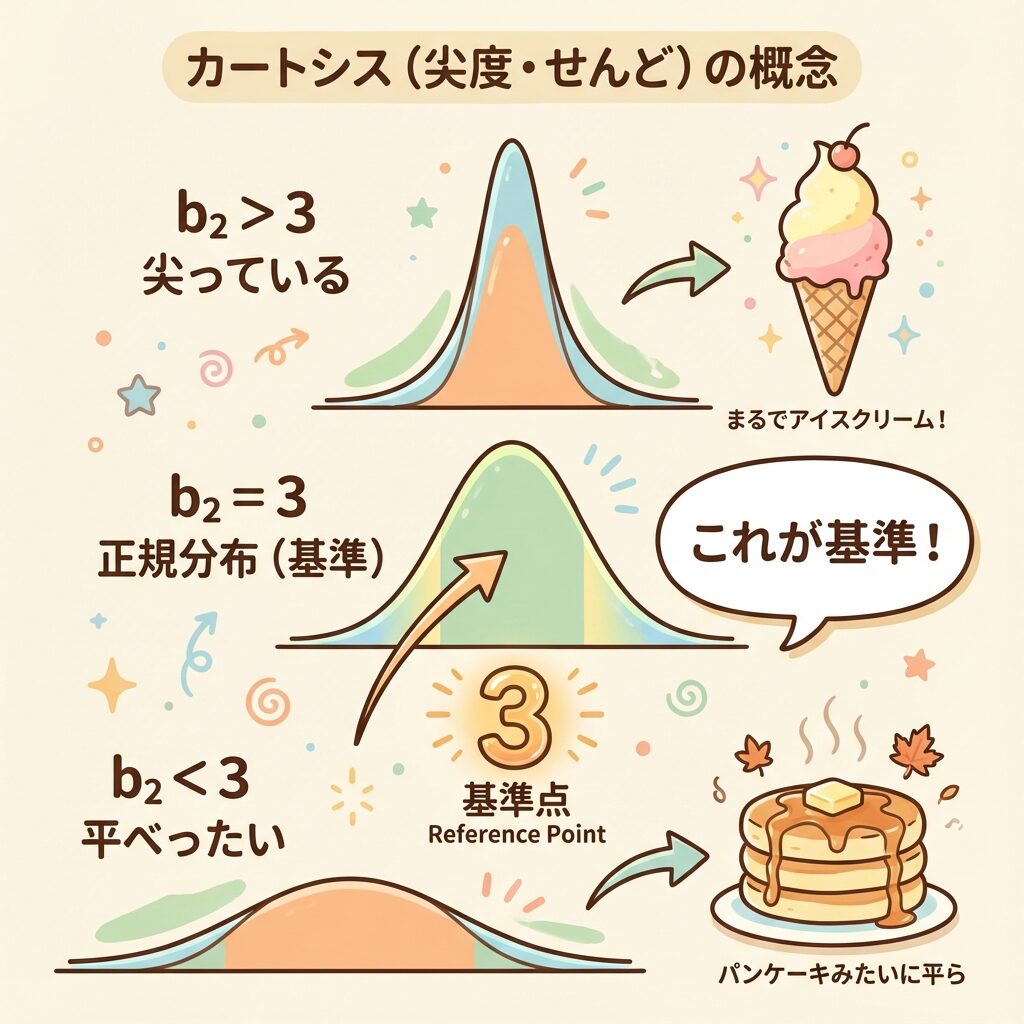
パターン1:正規分布と同じ(尖度 = 3)
正規分布のとがり具合が基準です。
尖度 b₂ = 3
標準的な山の形
パターン2:正規分布より尖っている(尖度 > 3)
山が鋭くとがっていて、裾が厚い(外れ値が出やすい)分布です。
尖度 b₂ > 3
ソフトクリームのように尖った形
パターン3:正規分布より平べったい(尖度 < 3)
山がなだらかで平べったく、裾が薄い(外れ値が出にくい)分布です。
尖度 b₂ < 3
パンケーキのように平べったい形
尖度の覚え方:「3」を基準に比較する
「尖度3 = 正規分布」をまず覚える!
- b₂ > 3 → 正規分布より尖っている(外れ値が出やすい)
- b₂ = 3 → 正規分布と同じ
- b₂ < 3 → 正規分布より平べったい(外れ値が出にくい)
なぜ「3」が基準なのか?(発展)
尖度の公式は「偏差の4乗の平均」を「標準偏差の4乗」で割ったものです。
正規分布でこの計算をすると、ちょうど3になることが数学的に証明されています。だから「3」が基準値なんです。
教科書によっては、「尖度 − 3」を使う場合があります。これを「超過尖度」と呼びます。
超過尖度の場合、正規分布 = 0 が基準になります。
QC検定では通常の尖度(正規分布 = 3)が使われることが多いので、問題文をよく確認しましょう。

正規分布の基準値を完璧に覚えよう
ここまでの内容を整理します。試験で絶対に覚えておくべき数値がこれです。
🔔 正規分布の基準値
| 歪度 √b₁ | 0 | 左右対称だから |
| 尖度 b₂ | 3 | これが基準値 |
語呂合わせで覚える
「歪度ゼロ、尖度サン(3)」
「わいどゼロ、せんどサン」とリズムで覚えましょう!
グラフから歪度・尖度を判断する方法
試験では、グラフを見て歪度・尖度を判断する問題がよく出ます。実際の問題を使って練習しましょう。
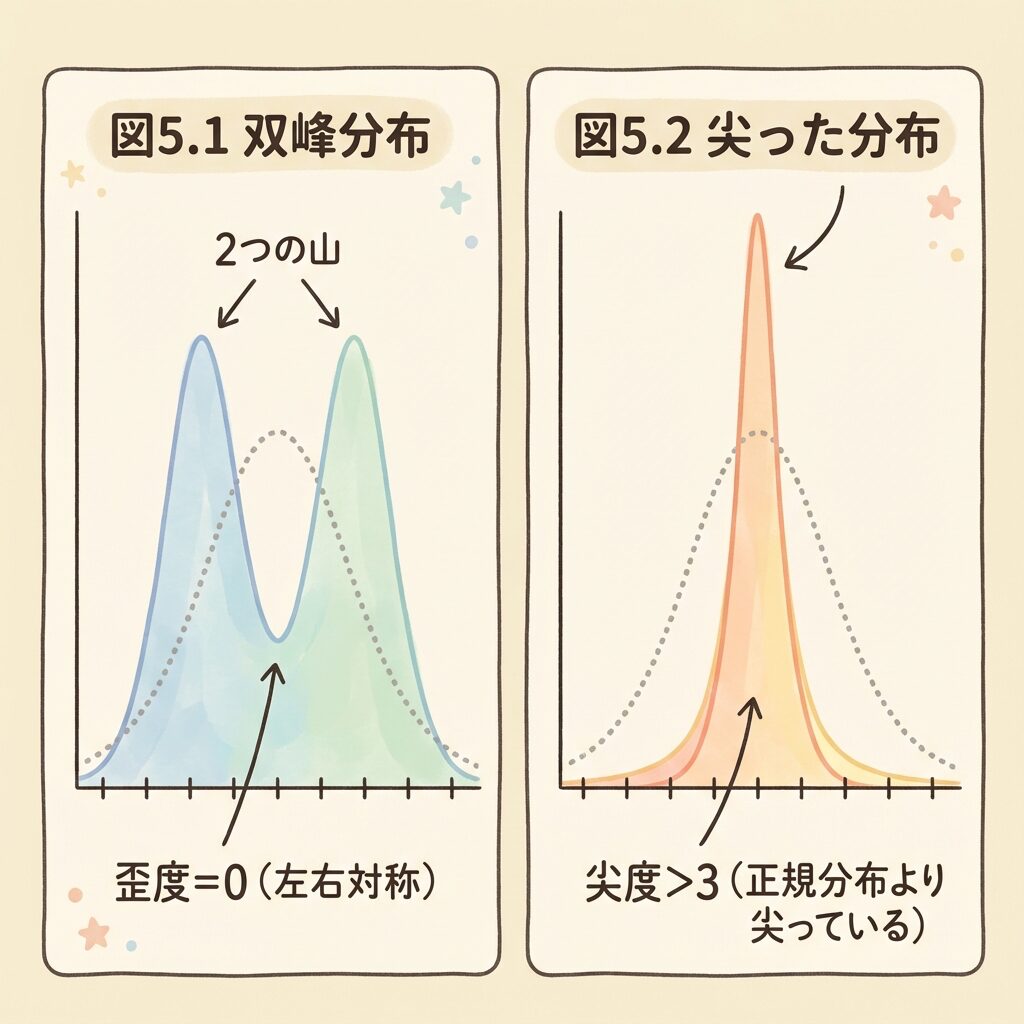
例題1:双峰分布(2つの山がある分布)
下図のような、2つの山がある分布(実線)の歪度はいくつ?
左の山 右の山
考え方:
- 2つの山が左右対称に配置されている
- 左右対称 → 歪度は0
答え:歪度 √b₁ = 0
例題2:尖った分布
下図のような、正規分布(点線)より尖っている分布(実線)の尖度は?
▲ ← 実線(尖っている)
/|\
/ | \
/ | \ ⌒ ← 点線(正規分布)
/ | \ / \
/ | \/ \
考え方:
- 実線は正規分布(点線)より尖っている
- 正規分布の尖度 = 3 が基準
- 尖っている → 尖度は3より大きい
答え:尖度 b₂ > 3(正規分布より大きな値)
グラフ判断のチェックリスト
| チェック項目 | 判断基準 |
|---|---|
| 歪度を判断するとき |
① 左右対称か? → 対称なら 0 ② どちらに裾が長い? → 右なら +、左なら − |
| 尖度を判断するとき |
① 正規分布(点線)と比較 ② 尖っている? → 3より大きい ③ 平べったい? → 3より小さい |
公式の意味を直感的に理解する(発展)
最後に、数式アレルギーの方でも理解できるように、公式の「意味」だけを解説します。
なぜ歪度は「3乗」を使うのか?
歪度の公式では、偏差(各データと平均の差)を3乗しています。
2乗だと符号が消えるからです。
- 2乗:(+3)² = 9、(-3)² = 9 → 同じ値になってしまう
- 3乗:(+3)³ = 27、(-3)³ = -27 → 符号が残る!
3乗することで、「右に偏っている(+)」「左に偏っている(−)」を区別できるんです。
なぜ尖度は「4乗」を使うのか?
尖度の公式では、偏差を4乗しています。
外れ値(平均から遠いデータ)を強調するためです。
- 偏差が2のデータ:2⁴ = 16
- 偏差が5のデータ:5⁴ = 625
4乗すると、外れ値の影響が極端に大きくなります。
だから、「裾が厚い(外れ値が多い)分布」を検出できるんです。
まとめ:歪度と尖度の完全攻略チェックリスト
✅ 歪度(√b₁)のポイント
| √b₁ = 0 | 左右対称 |
| √b₁ > 0 | 右に裾が長い(正の歪み) |
| √b₁ < 0 | 左に裾が長い(負の歪み) |
✅ 尖度(b₂)のポイント
| b₂ = 3 | 正規分布と同じ(基準) |
| b₂ > 3 | 正規分布より尖っている |
| b₂ < 3 | 正規分布より平べったい |
✅ 絶対に覚える数値
正規分布 → 歪度 = 0、尖度 = 3
- グラフ問題では、まず「正規分布(点線)と比較」することを意識
- 歪度は「裾がどちらに長いか」で符号を判断
- 尖度は「3と比較して大きいか小さいか」で判断
- 「歪度ゼロ、尖度サン」と覚えておけば、計算問題でも慌てない
📚 次に読むべき記事
歪度・尖度の基準となる正規分布を深く理解しましょう
歪度・尖度の計算に必要な分散の基礎を確認
正規性の確認後に行う検定の選び方を学ぶ

