- R²(決定係数)の意味がなんとなくしかわからない
- 「寄与率」「決定係数」「説明率」…呼び方が多すぎて混乱する
- 自由度調整済み寄与率がなぜ必要なのかわからない
- R²=0.8って「良い」の?「悪い」の?基準がわからない
- 公式を見ても、なぜその式になるのか理解できない
- 寄与率(R²)の直感的な意味と「バラつきの分解」という考え方
- 決定係数・寄与率・説明率など呼び方が複数ある理由
- 自由度調整済み寄与率(R̄²)がなぜ必要か
- R²の計算式の導出と「なぜその式になるか」
- R²の値の解釈と注意点
目次
結論:寄与率R²は「予測がどれだけ当たっているか」の指標
いきなり結論からお伝えします。
寄与率(R²)とは、「データ全体のバラつきのうち、回帰式(予測式)でどれだけ説明できているか」を0〜1の数値で表したものです。
R² = 0.85
「データのバラつきの85%は、この回帰式で説明できる」
「残り15%は、説明できない誤差(残差)」
つまり、R²が1に近いほど「予測が当たっている」、0に近いほど「予測が当たっていない」ということです。
この指標がなぜ重要なのか、なぜこの式になるのか、これから順を追って解説していきます。
まず「バラつきの分解」を理解しよう
寄与率R²を理解するには、「バラつきを分解する」という考え方が鍵になります。
🎯 回帰分析の目的を思い出す
回帰分析では、「yを予測したい」というのが目的です。例えば:
- 勉強時間(x)からテストの点数(y)を予測したい
- 広告費(x)から売上(y)を予測したい
- 気温(x)からアイスの売上(y)を予測したい
そして、最小二乗法で回帰直線 ŷ = a + bx を求めます。
でも、ここで疑問が生まれます。
「この回帰直線、どれくらい信頼できるの?」
「予測式を作ったけど、本当に当たるの?」
この疑問に答えるのが、寄与率R²です。
📊 yのバラつきを「2つの成分」に分解する
ここからが核心です。yのバラつき(変動)は、2つの成分に分解できます。
具体的に、あるデータ点を考えてみましょう。実際の値がyᵢ、回帰式による予測値がŷᵢ、全データの平均がȳだとします。
①「平均からのズレ」=全体のバラつき
yᵢ − ȳ(実際の値と平均の差)
②「平均から予測値までのズレ」=回帰で説明できる部分
ŷᵢ − ȳ(予測値と平均の差)
③「予測値から実際の値までのズレ」=説明できない部分(残差)
yᵢ − ŷᵢ(実際の値と予測値の差)
そして、この3つには以下の関係があります。
📐 平方和の分解:ST = SR + Se
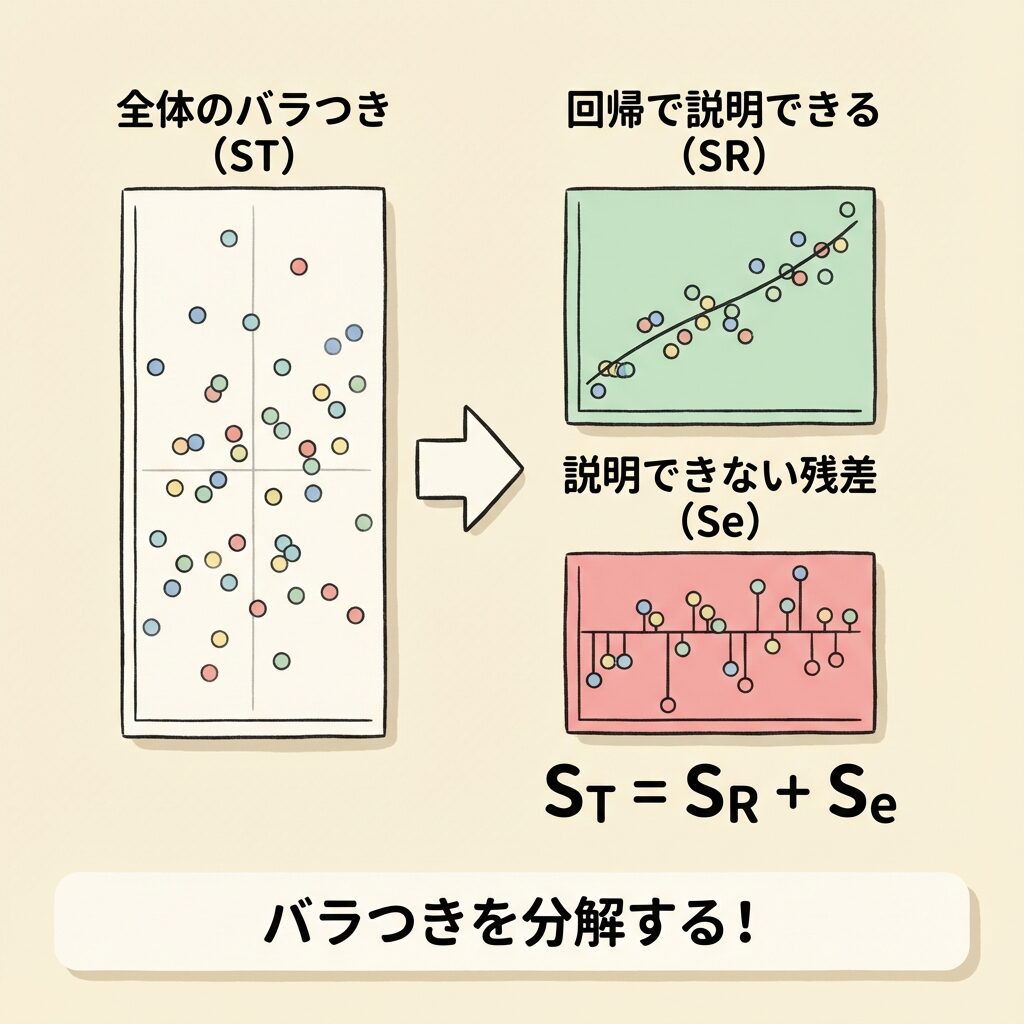
上の式を全データについて2乗して合計すると、平方和の分解式になります。
ST = SR + Se
| ST(総平方和) | Σ(yᵢ − ȳ)² | データ全体のバラつき |
| SR(回帰平方和) | Σ(ŷᵢ − ȳ)² | 回帰式で説明できるバラつき |
| Se(残差平方和) | Σ(yᵢ − ŷᵢ)² | 説明できないバラつき(誤差) |
つまり、「yの全体的なバラつき」は「回帰で説明できる部分」と「説明できない部分」に分けられるということです。
パイ(ST)を2つに切り分けるイメージです。
🥧 SR(緑の部分):「xのおかげでyを説明できた部分」
🥧 Se(赤の部分):「xだけでは説明できなかった部分」
SRの割合が大きいほど、「xでyをよく説明できている」ことになります。
寄与率R²の定義:「説明できた割合」
ここまで理解できれば、寄与率R²の定義は簡単です。
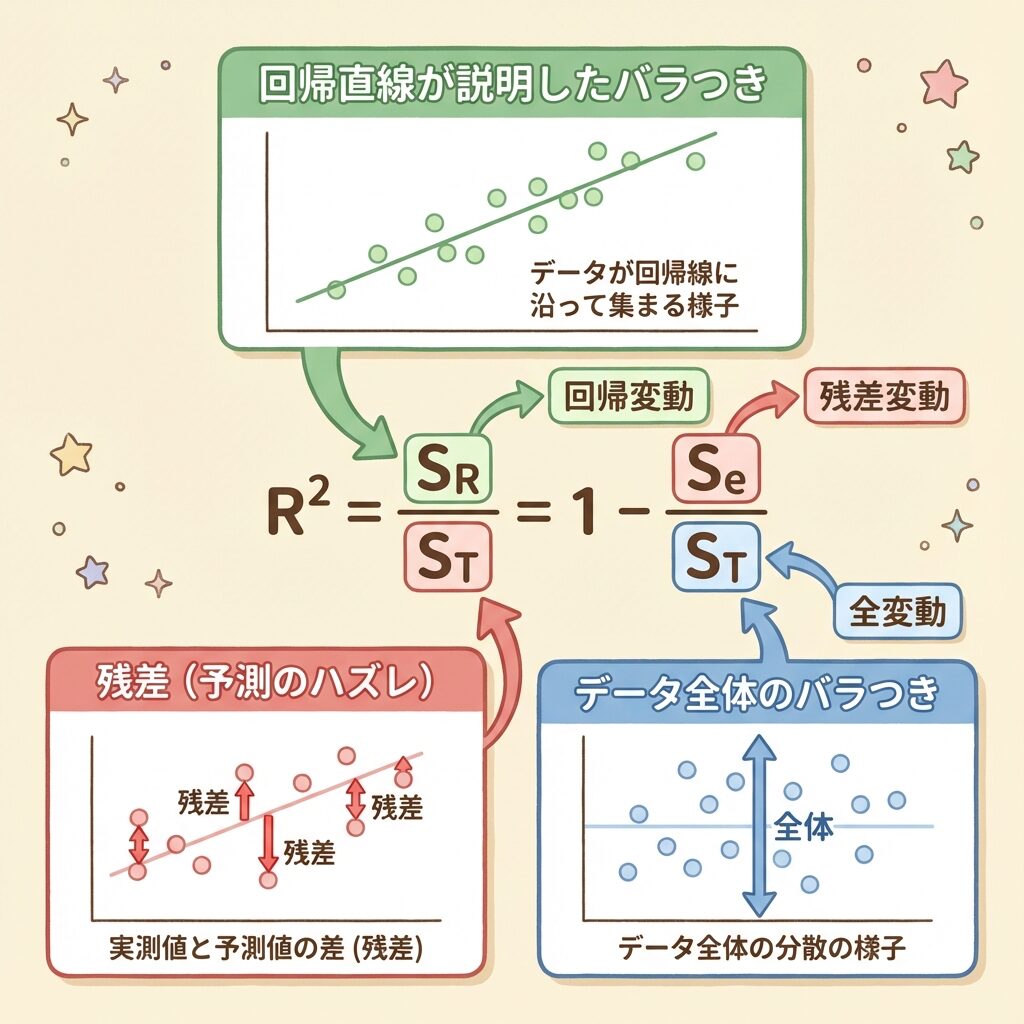
R² = 回帰で説明できたバラつき ÷ 全体のバラつき
この式の意味を言葉で表すと:
「yの全体的なバラつきのうち、xで説明できた割合」
または
「1 − 説明できなかった割合」
R²の値の解釈:0から1の間で「当てはまりの良さ」を表す
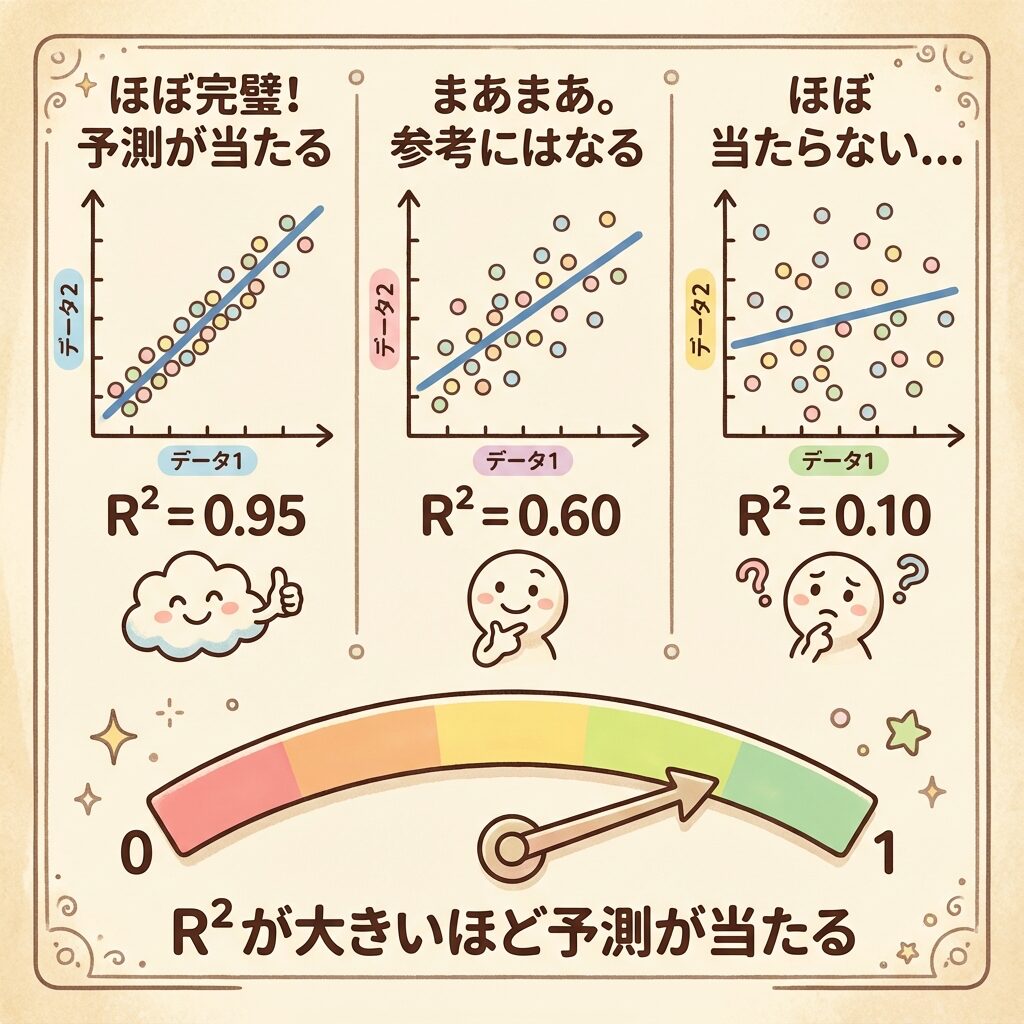
R²は0以上1以下の値を取ります。それぞれの意味を見てみましょう。
🎯 R²の値と意味
| R²の値 | 意味 | イメージ |
|---|---|---|
| R² = 1.00 | 完璧な予測。すべてのデータが回帰直線上にある | 🎯 100%的中 |
| R² = 0.90〜0.99 | 非常に高い説明力。予測がよく当たる | 😄 優秀 |
| R² = 0.70〜0.89 | 高い説明力。実用的に使える場合が多い | 🙂 良い |
| R² = 0.50〜0.69 | 中程度の説明力。参考にはなるが注意が必要 | 😐 まあまあ |
| R² = 0.00〜0.49 | 低い説明力。xとyの関係が弱い | 😢 改善が必要 |
| R² = 0.00 | xではyを全く説明できない | ❌ 関係なし |
上の表はあくまで目安です。
・物理実験:R² = 0.99以上が期待されることも
・社会科学:R² = 0.30でも「関係あり」と判断されることも
・品質管理:R² = 0.80以上が望ましいことが多い
分野や目的に応じて判断基準を変える必要があります。
「決定係数」「寄与率」「説明率」…呼び方が多い理由
ここで、多くの人が混乱するポイントを整理しておきましょう。R²には複数の呼び方があります。
| 呼び方 | 主に使われる分野 | 英語 |
|---|---|---|
| 決定係数 | 統計学、データサイエンス | Coefficient of Determination |
| 寄与率 | 品質管理、QC検定、実験計画法 | Contribution Ratio |
| 説明率 | 一部の教科書 | Explanation Ratio |
| R²(アールスクエア) | 共通 | R-squared |
呼び方が違うだけで、計算方法も意味も全く同じです。
・統計学の本を読むとき → 「決定係数」
・QC検定の勉強をするとき → 「寄与率」
・論文やソフトウェア → 「R²」
と呼ばれているだけなので、混乱しないでください。
🤔 なぜ呼び方が複数あるの?
歴史的な経緯と、分野ごとの文化の違いが原因です。
「決定係数」の由来:
英語の "Coefficient of Determination" の直訳。「yの値を決定する度合い」という意味合い。統計学の世界で広く使われる。
「寄与率」の由来:
日本の品質管理・実験計画法の分野で発展。「各因子がどれだけ寄与(貢献)しているか」を表す割合という意味。QC検定ではこちらが主流。
「R²」の由来:
相関係数rの2乗に等しいことから。単回帰分析では R² = r² が成り立つため、この表記が広まった。
R²の落とし穴:変数を増やすと必ず上がる問題
ここからは、R²の重大な欠点について説明します。これを知らないと、誤った判断をしてしまう可能性があります。
📈 説明変数を増やすとR²は「必ず」上がる
重回帰分析(説明変数が複数ある回帰分析)では、説明変数を増やせば増やすほど、R²は必ず大きくなります。絶対に下がりません。
売上(y)を予測したいとして…
・広告費(x₁)だけで予測 → R² = 0.60
・広告費 + 気温(x₂)で予測 → R² = 0.65
・広告費 + 気温 + 社長の年齢(x₃)で予測 → R² = 0.66
「社長の年齢」は売上と関係ないはずなのに、入れるとR²が上がってしまう!
なぜこうなるかというと、どんな変数でも「偶然の一致」で少しは説明できてしまうからです。
データが100個あれば、無関係な変数でも偶然yと少し相関することがあります。その「偶然の相関」もR²に加算されてしまうのです。
🤔 これの何が問題?
「R²が高い=良いモデル」と単純に考えると、以下の問題が起きます。
- 無意味な変数を入れてもR²が上がるので、本当に重要な変数がわからなくなる
- 過学習(オーバーフィッティング)が起きやすくなる
- 新しいデータに対する予測精度が落ちる
この問題を解決するために生まれたのが、自由度調整済み寄与率(R̄²)です。
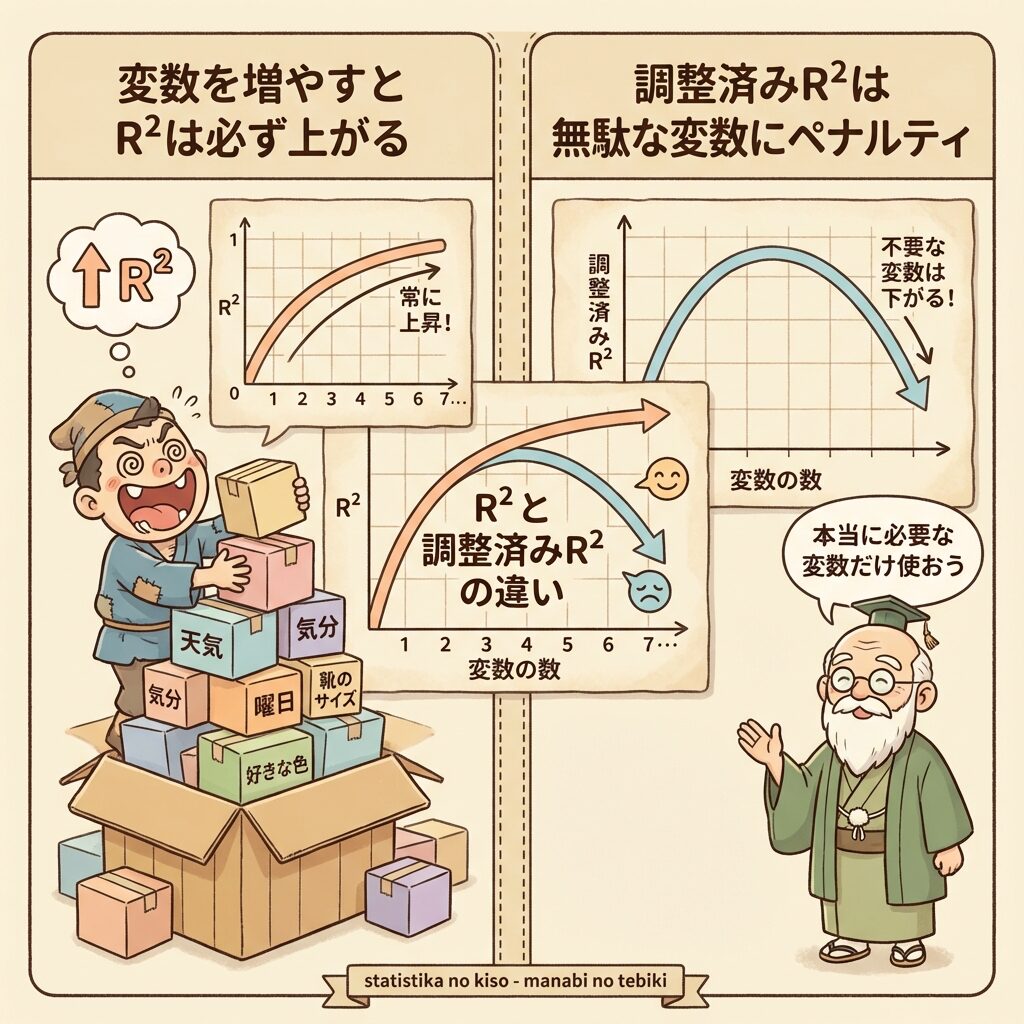
自由度調整済み寄与率(R̄²):無駄な変数にペナルティを与える
自由度調整済み寄与率(Adjusted R²、R̄²)は、「変数を増やすと必ずR²が上がる」問題を解決するために考案されました。
📐 自由度調整済みR²の公式
n:データ数 / p:説明変数の数
これを変形すると、以下の形にもなります。
🤔 この式の意味は?
普通のR²との違いを見てみましょう。
| 指標 | 分母で使う自由度 | 特徴 |
|---|---|---|
| R² | Se, ST をそのまま使う | 変数を増やすと必ず上がる |
| R̄² | Se÷(n−p−1), ST÷(n−1) | 無駄な変数を入れると下がることもある |
ポイントは、分母の (n − p − 1) の部分です。
説明変数pを増やすと、n − p − 1 が小さくなる。
すると Se÷(n−p−1) は大きくなる(分母が小さくなるから)。
つまり、「変数を増やすと、残差の"見かけ上の"減少分にペナルティがかかる」仕組みになっています。
本当に意味のある変数を追加すれば → Seの減少がペナルティを上回り → R̄²は上がる
無意味な変数を追加すると → Seの減少がペナルティを下回り → R̄²は下がる
📊 R²とR̄²の比較例
具体的な数値で見てみましょう。データ数n=100とします。
| モデル | 変数の数 p | R² | R̄² | 判断 |
|---|---|---|---|---|
| 広告費のみ | 1 | 0.600 | 0.596 | — |
| 広告費+気温 | 2 | 0.720 | 0.714 | ✅ 改善 |
| 広告費+気温+社長の年齢 | 3 | 0.722 | 0.713 | ❌ 悪化 |
R²だけ見ると「社長の年齢を入れた方が良い」ように見えますが、R̄²を見ると「入れない方が良い」とわかります。これが自由度調整の威力です。
R²とR̄²、どちらを使うべき?
結論から言うと、状況によって使い分けるのがベストです。
| 状況 | おすすめ | 理由 |
|---|---|---|
| 単回帰分析(変数1つ) | R²でOK | 変数が1つなので調整の必要なし |
| 重回帰分析(変数複数) | R̄²を優先 | 変数選択の判断に使える |
| モデル同士の比較 | R̄²を優先 | 変数の数が違っても公平に比較できる |
| QC検定の問題 | 問題文に従う | 「寄与率」と「自由度調整済み寄与率」は別々に出題される |
R²の注意点:高ければ良いわけではない
最後に、R²を使う上での重要な注意点をまとめます。
⚠️ 注意点①:R²が高くても因果関係は証明できない
R²=0.95でも、「xがyの原因である」とは言えません。あくまで「相関が強い」というだけです。
「アイスの売上」と「水難事故」のR²が高い
→ 「アイスを売ると事故が起きる」わけではない!
→ 両方とも「気温」という第三の要因に影響されているだけ(擬似相関)
⚠️ 注意点②:外れ値に弱い
極端な外れ値が1つあるだけで、R²が大きく変わることがあります。必ず散布図を確認し、外れ値の影響をチェックしましょう。
⚠️ 注意点③:非線形な関係には対応できない
R²は「直線でどれだけ説明できるか」を測っています。曲線的な関係がある場合、R²が低くても「関係がない」とは限りません。
⚠️ 注意点④:サンプルサイズが小さいと不安定
データが少ないと、R²の値は不安定になります。たまたまR²=0.90になっても、データを増やすと大きく変わることがあります。
計算例:実際にR²を求めてみよう
最後に、具体的な数値でR²を計算してみましょう。
📝 例題
以下のデータについて、寄与率R²を求めなさい。
- 総平方和 ST = 200
- 残差平方和 Se = 50
✍️ 解答
R² = 1 − Se/ST の公式を使います。
R² = 1 − Se/ST
= 1 − 50/200
= 1 − 0.25
= 0.75
答え:R² = 0.75(75%)
これは「yの全体的なバラつきのうち、75%は回帰式で説明できている」という意味です。残り25%は説明できない残差です。
まとめ:寄与率R²の完全理解
- 寄与率R²は「yのバラつきのうち、回帰式で説明できた割合」
- R² = SR/ST = 1 − Se/ST(0〜1の値を取る)
- R²が1に近いほど「予測が当たっている」、0に近いほど「当たっていない」
- 「決定係数」「寄与率」「説明率」は全部同じもの(分野による呼び方の違い)
- 重回帰分析では、変数を増やすとR²は必ず上がる(欠点)
- 自由度調整済み寄与率R̄²は、無駄な変数にペナルティを与える改良版
- R²が高くても因果関係は証明できない、外れ値に注意、非線形には対応できない
寄与率(決定係数)は、回帰分析の「通信簿」のようなものです。この予測モデルがどれくらい信頼できるかを、0から1の数値で教えてくれます。
ただし、R²だけを見て判断するのは危険です。散布図を描いて視覚的に確認する、残差分析を行う、因果関係と相関関係を混同しないなど、総合的な判断が大切です。
📚 次に読むべき記事
R²だけでなく、回帰係数の有意性も確認しましょう
ST, SR, Seの計算方法を詳しく学べます
回帰分析全体の学習順序がわかります