- E(X+Y) と V(X+Y) の公式がごちゃごちゃになる
- 「独立」と「独立でない」で公式が変わるのが混乱する
- 共分散と相関係数の関係がわからない
- QC検定の「和・差の分散」の問題が解けない
- 期待値・分散の公式を図解で完全理解
- 「独立」と「独立でない」の違いを水槽のたとえで直感的に
- 共分散・相関係数の関係を1枚の図で整理
- 実際の計算例で手を動かしてマスター
目次
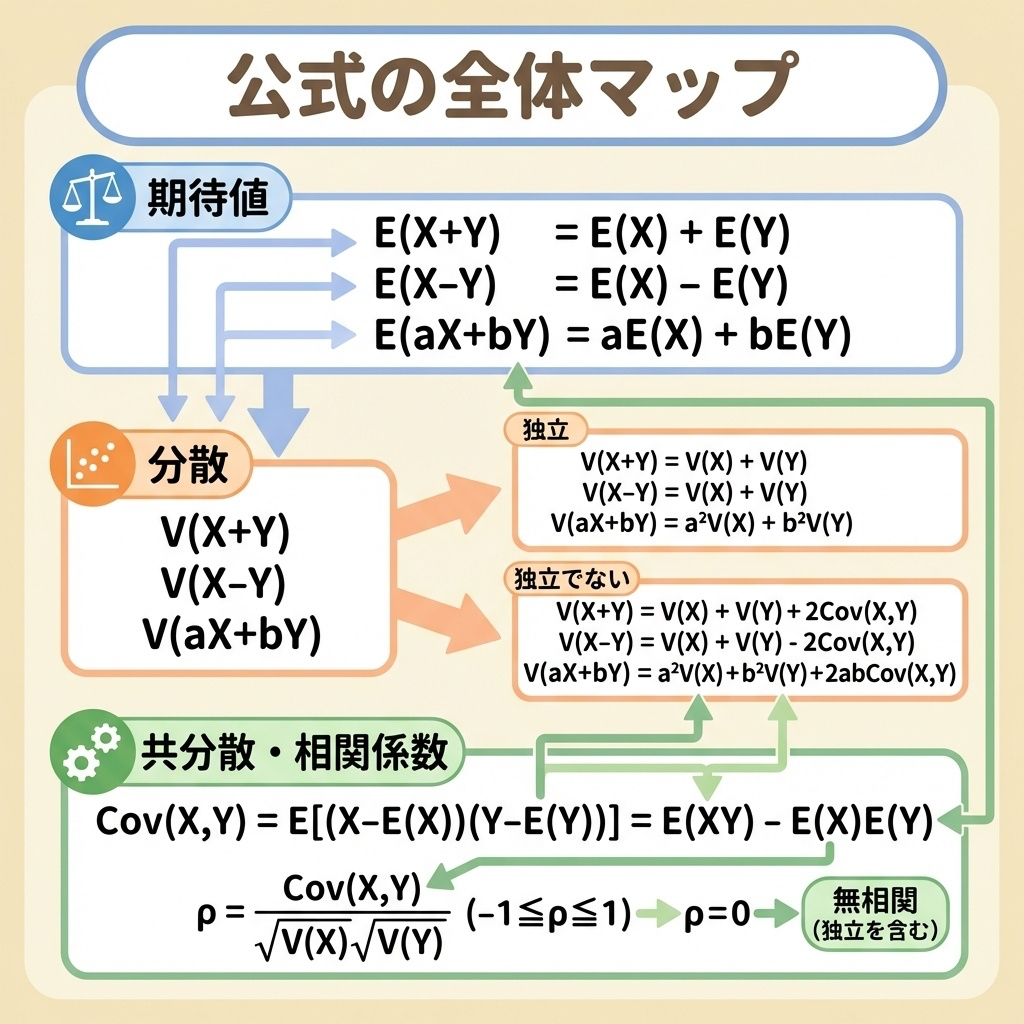
この記事の全体像|何を学ぶのか?
確率変数の「和や差」を扱う問題では、以下の3つの知識が必要です。
| テーマ | ポイント | 難易度 |
|---|---|---|
| ① 期待値の計算 | 単純に足し引きするだけ(独立関係なし) | ★☆☆ |
| ② 分散の計算 | 独立なら足す、独立でないなら共分散を加える | ★★☆ |
| ③ 共分散と相関係数 | 「連動の度合い」を測る指標 | ★★★ |
この記事では、図解を中心にこれらの概念を順番に解説していきます。
① 期待値の計算|独立かどうかは関係ない!
期待値(平均)の計算は、実はとてもシンプルです。
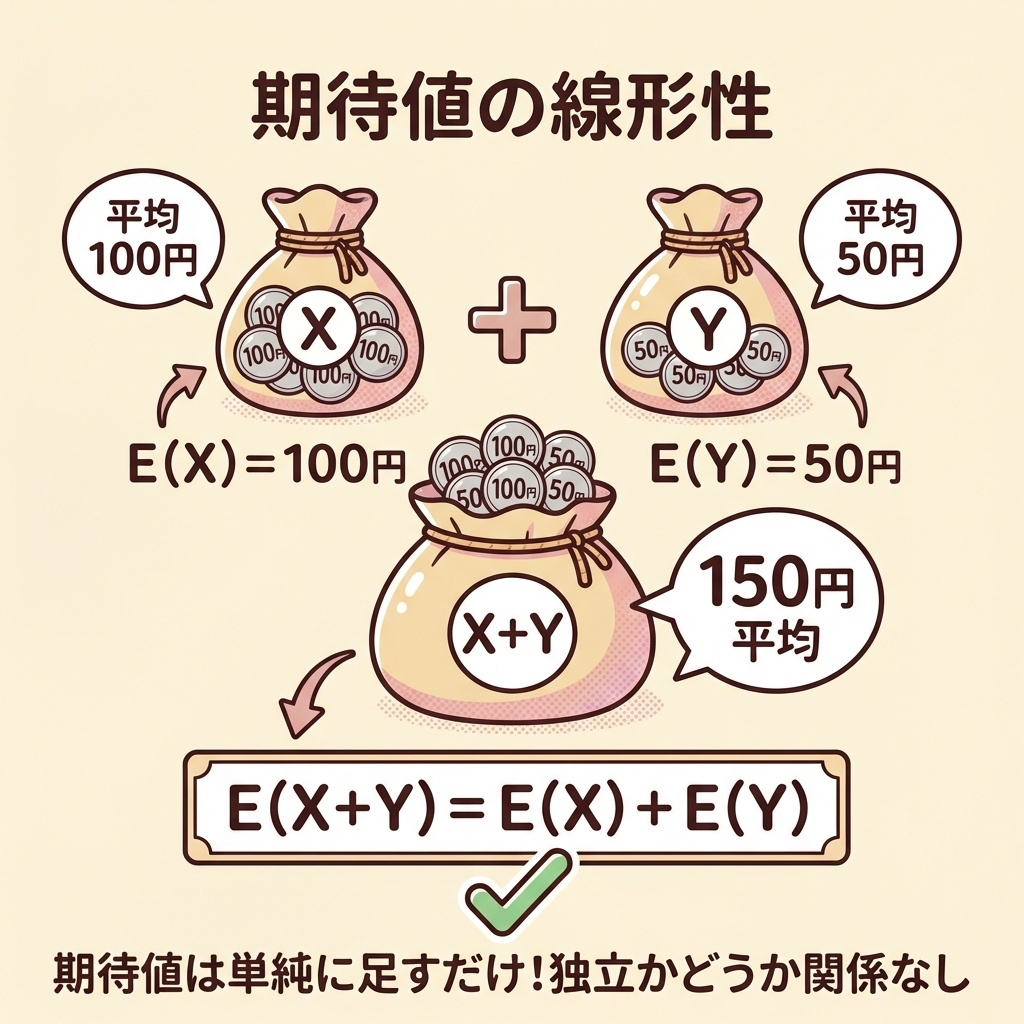
期待値の線形性|足し算・引き算はそのまま
※ a, b は定数。独立かどうかに関係なく成り立つ!
袋Xには平均100円、袋Yには平均50円のコインが入っているとします。
両方の袋を合わせたら? → 平均は 100 + 50 = 150円
「袋同士が関係あるかどうか」は、平均の計算には影響しません。
これが期待値の線形性です。
第8回:期待値 - 確率分布の中心を知る →
② 分散の計算|「独立かどうか」で公式が変わる!
分散の計算は、期待値と違って「独立かどうか」が重要になります。
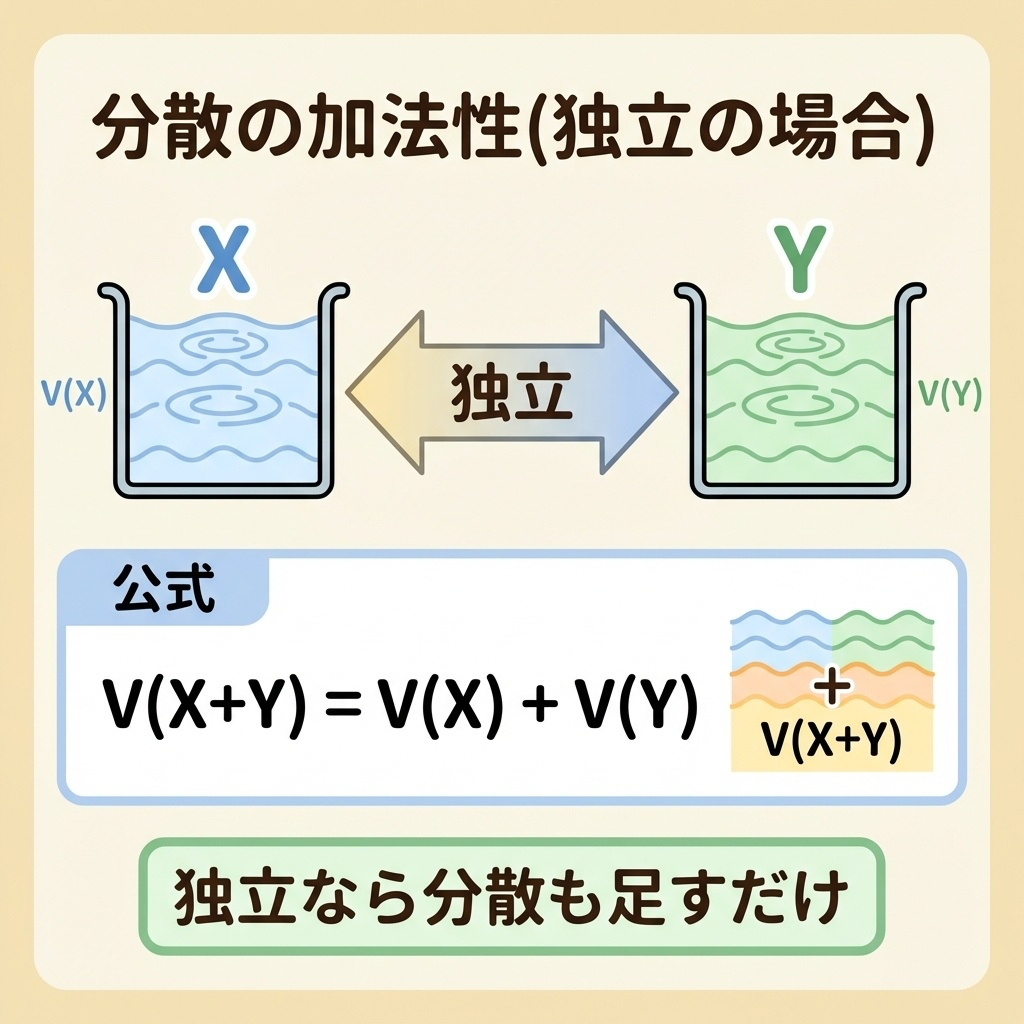
ケース①:XとYが独立の場合
2つの確率変数が独立(互いに影響しない)なら、分散は単純に足すだけです。
⚠️ 引き算でも分散は「足す」!(バラつきは打ち消し合わない)
2つの水槽が完全に別々に置かれていると想像してください。
それぞれの水槽の波(バラつき)は、互いに影響しません。
2つを合わせたときの「総合的な波の大きさ」は、単純に足し算になります。
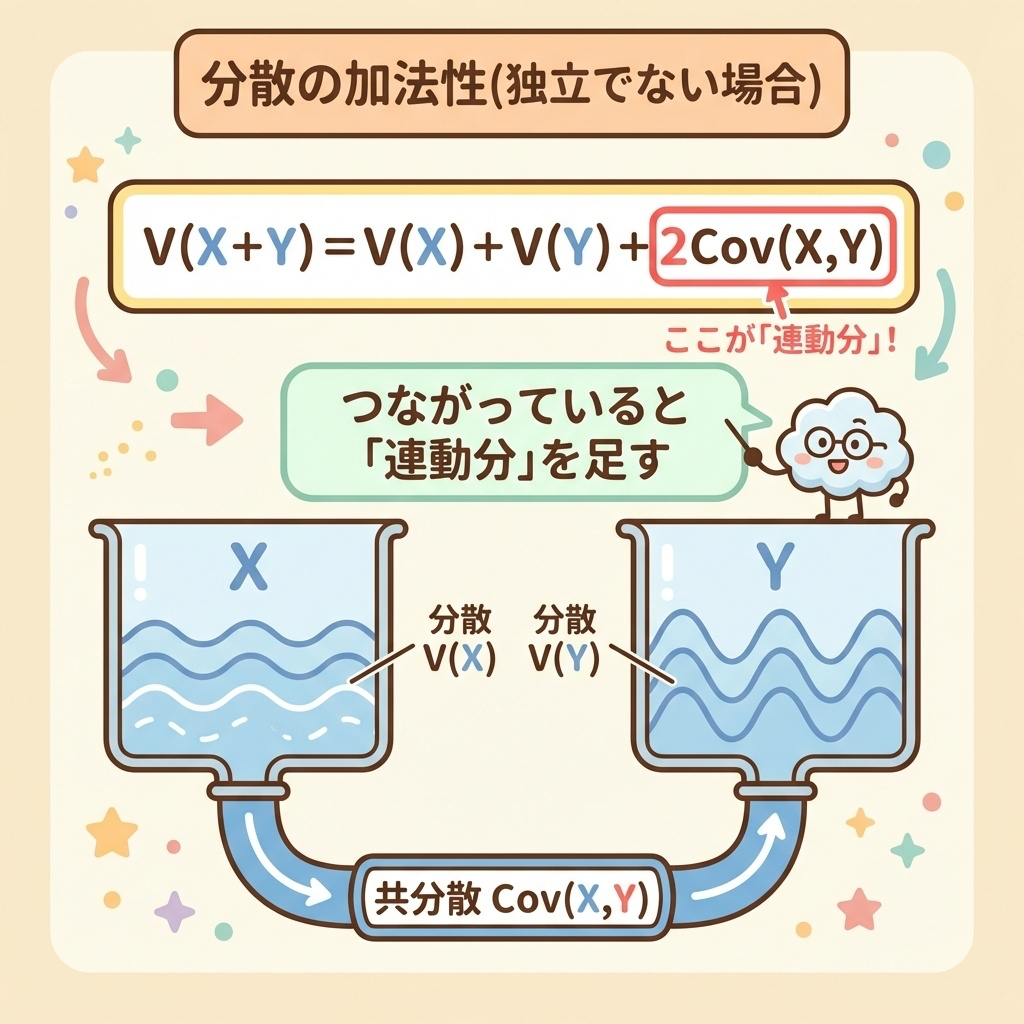
ケース②:XとYが独立でない場合(ここが重要!)
2つの確率変数が独立でない(互いに影響する)場合、共分散という「連動の度合い」を加える必要があります。
※ Cov(X, Y) は共分散。正なら波が同調、負なら波が逆位相。
2つの水槽がパイプでつながっていると想像してください。
片方の波が起きると、もう片方にも影響します(連動する)。
この「連動分」が共分散です。
・同じ方向に波立つ(正の共分散)→ 合計のバラつきは大きくなる
・逆方向に波立つ(負の共分散)→ 合計のバラつきは小さくなる
V(X+Y) を展開すると、共分散の項が2回出てくるからです。
V(X+Y) = E[(X+Y-μx-μy)²]
= E[(X-μx)² + 2(X-μx)(Y-μy) + (Y-μy)²]
= V(X) + 2Cov(X,Y) + V(Y)
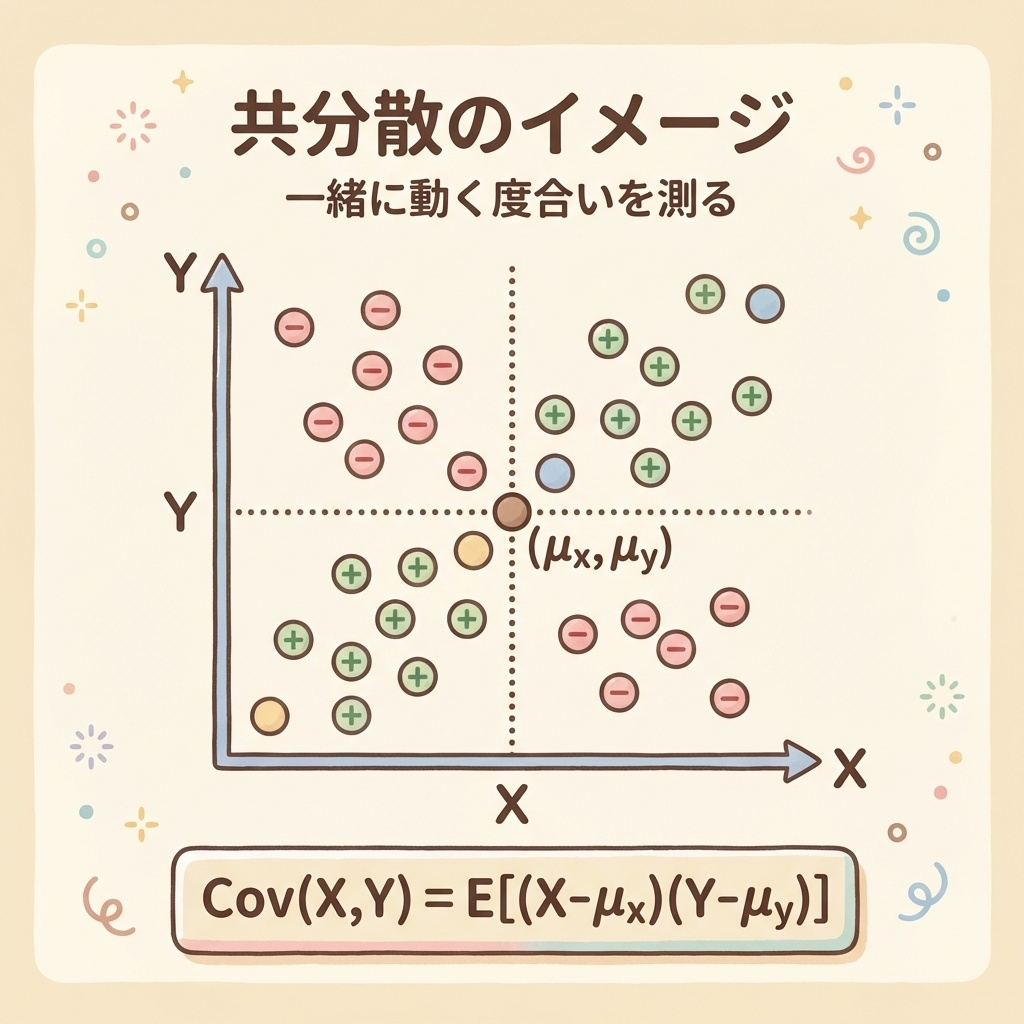
③ 共分散とは?|「一緒に動く度合い」を測る
共分散は、2つの変数が一緒に動く傾向を数値化したものです。
共分散の定義と直感的な意味
| 共分散の値 | 意味 | イメージ |
|---|---|---|
| Cov > 0 | 正の関係 | Xが増えるとYも増える傾向 |
| Cov < 0 | 負の関係 | Xが増えるとYは減る傾向 |
| Cov = 0 | 無相関 | XとYは連動しない(独立の可能性) |
独立ならば Cov(X,Y) = 0 です。
しかし逆は成り立ちません! Cov(X,Y) = 0 でも独立とは限らないのです。
(非線形な関係がある場合など)
④ 相関係数とは?|共分散を「比較可能」にする
共分散には1つ大きな問題があります。それは「単位がある」こと。値の大きさだけで「強い関係」とは言えません。
そこで、共分散を標準偏差で割って正規化したものが相関係数です。
相関係数の定義
範囲:−1 ≤ ρ ≤ 1
共分散と相関係数の関係(公式変形)
相関係数の式を変形すると、共分散は以下のように表せます。
問題では「相関係数ρ」が与えられることが多いので、この変換が超重要!
問題文で「相関係数ρ = 0.6」のように与えられたら、
Cov(X,Y) = ρ × σX × σY で共分散を求めて、
それを V(X+Y) = V(X) + V(Y) + 2Cov(X,Y) に代入します。

公式の全体まとめ|これだけ覚えればOK!
期待値の公式(独立・非独立 共通)
| E(X + Y) | = E(X) + E(Y) |
| E(X − Y) | = E(X) − E(Y) |
| E(aX + bY) | = aE(X) + bE(Y) |
| E(aX) | = aE(X) |
分散の公式(独立の場合)
| V(X + Y) | = V(X) + V(Y) |
| V(X − Y) | = V(X) + V(Y) |
| V(aX) | = a²V(X) |
| V(aX + bY) | = a²V(X) + b²V(Y) |
分散の公式(独立でない場合)
| V(X + Y) | = V(X) + V(Y) + 2Cov(X,Y) |
| V(X − Y) | = V(X) + V(Y) − 2Cov(X,Y) |
| V(aX + bY) | = a²V(X) + b²V(Y) + 2abCov(X,Y) |
※ Cov(X,Y) = ρ × σX × σY で計算
共分散・相関係数の公式
| Cov(X, Y) | = E(XY) − E(X)E(Y) |
| Cov(X, Y) | = ρ × σX × σY |
| ρ(相関係数) | = Cov(X,Y) ÷ (σX × σY) |
| Cov(aX, bY) | = ab × Cov(X, Y) |
【実践】計算例で手を動かそう
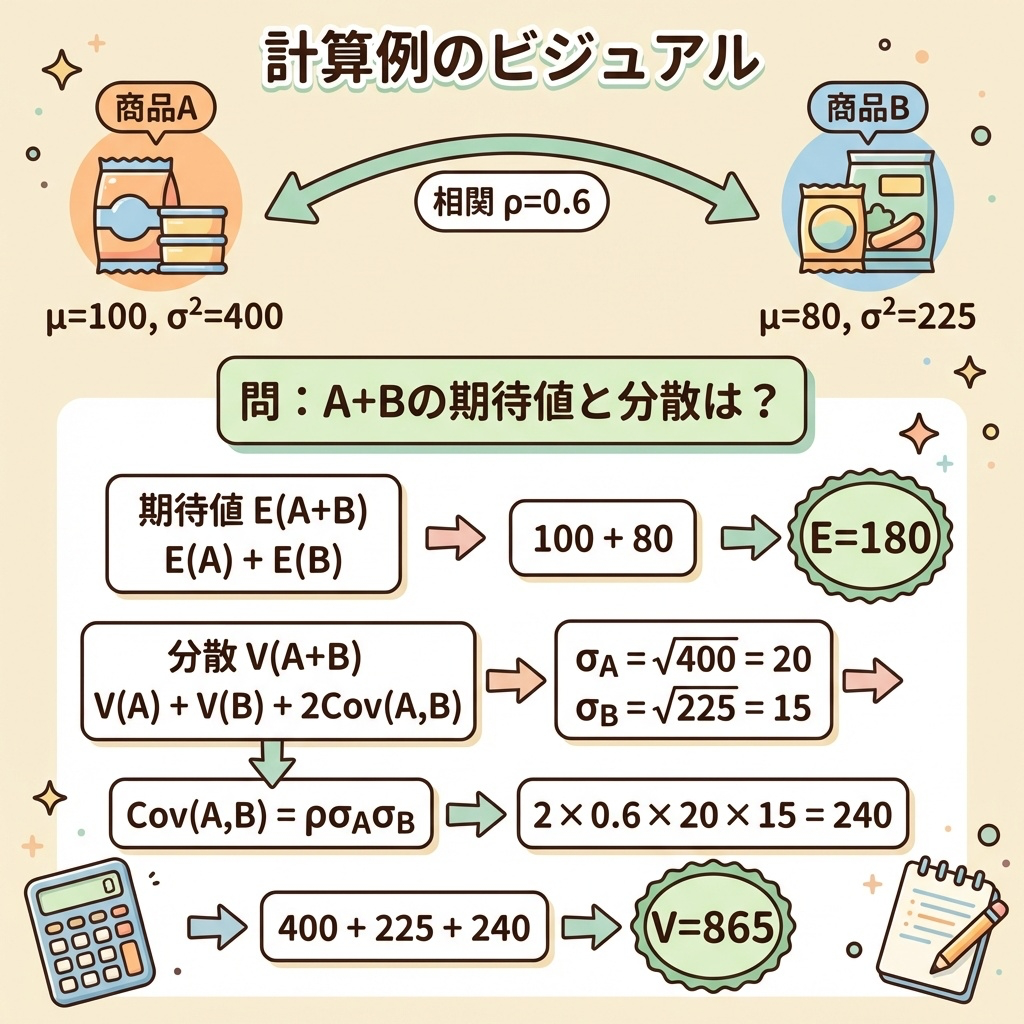
例題:2つの商品の合計利益
ある会社が商品Aと商品Bを販売しています。それぞれの利益は以下の確率分布に従います。
| 商品 | 期待値 E | 分散 V | 標準偏差 σ |
|---|---|---|---|
| 商品A (X) | 100万円 | 400 | 20 |
| 商品B (Y) | 80万円 | 225 | 15 |
2つの商品の利益には相関係数 ρ = 0.6 の関係があります(景気が良いと両方売れるなど)。
問:合計利益 X + Y の期待値と分散を求めよ。
Step 1:期待値を求める
E(X + Y) = E(X) + E(Y)
= 100 + 80
= 180万円
期待値は単純に足すだけなので、相関係数は使いません。
Step 2:共分散を求める
Cov(X, Y) = ρ × σX × σY
= 0.6 × 20 × 15
= 180
Step 3:分散を求める
V(X + Y) = V(X) + V(Y) + 2Cov(X, Y)
= 400 + 225 + 2 × 180
= 400 + 225 + 360
= 985
E(X + Y) = 180万円
V(X + Y) = 985(標準偏差 ≒ 31.4万円)
V(X + Y) = 400 + 225 = 625
正の相関があると、分散は 625 → 985 と大きくなります。
「景気が良いと両方売れる」ので、リスク(バラつき)も連動して大きくなるのです。
よくある間違いパターン
| ❌ 間違い | ⭕ 正しい |
|---|---|
| V(X−Y) = V(X) − V(Y) | V(X−Y) = V(X) + V(Y) 分散は引き算でも足す! |
| V(2X) = 2V(X) | V(2X) = 4V(X) 定数は2乗される! |
| 独立でないのに共分散を忘れる | +2Cov(X,Y) を忘れずに! 問題文の「相関係数」に注目 |
| σ(標準偏差)をそのまま足す | 分散に変換してから足す! σ² = V の関係を使う |
まとめ|この記事のポイント
- 期待値:独立かどうか関係なく、そのまま足し引き
- 分散(独立):引き算でも分散は「足す」
- 分散(独立でない):+2Cov(X,Y) を加える
📚 次に読むべき記事
より実践的な「部品の寸法公差」の問題を解いてみよう
「独立の場合」の分散をより深く理解する
共分散の概念をもっと詳しく学ぶ
