📊 この記事を読んでいるあなたへ
「X̄-R管理図以外にも種類があるの?」
「X-RsとかMe-Rとか、違いがよくわからない…」
「どんな時にどれを使うの?」
大丈夫です。この記事では、温泉旅館の温度管理を例に、3つの管理図の違いと使い分けをわかりやすく解説します!
目次
🎯 この記事でわかること
✅ X-Rs管理図(個々の値と移動範囲)の計算方法
✅ Me-R管理図(メディアンと範囲)の計算方法
✅ X̄-s管理図(平均と標準偏差)の計算方法
✅ 4つの管理図の使い分けフローチャート
✅ QC検定で出る計算問題の解き方
📍 シリーズ全体像|今ここ!
管理図シリーズ(全12記事)
① ロードマップ → ② バラつき入門 → ③ 管理図とは → ④ 種類一覧 → ⑤ 異常判定ルール → ⑥ 読み方・活用法 → ⑦ X̄-R管理図
⑧ X-Rs・Me-R・X̄-s管理図 ← 今ここ!
→ ⑨ np・p管理図 → ⑩ c・u管理図 → ⑪ Cp・Cpk → ⑫ 判定基準
💡 前の記事を読んでいない方へ
X̄-R管理図の基本がわからない方は、先にこちらの記事をご覧ください。

🗺️ まず全体像を押さえよう
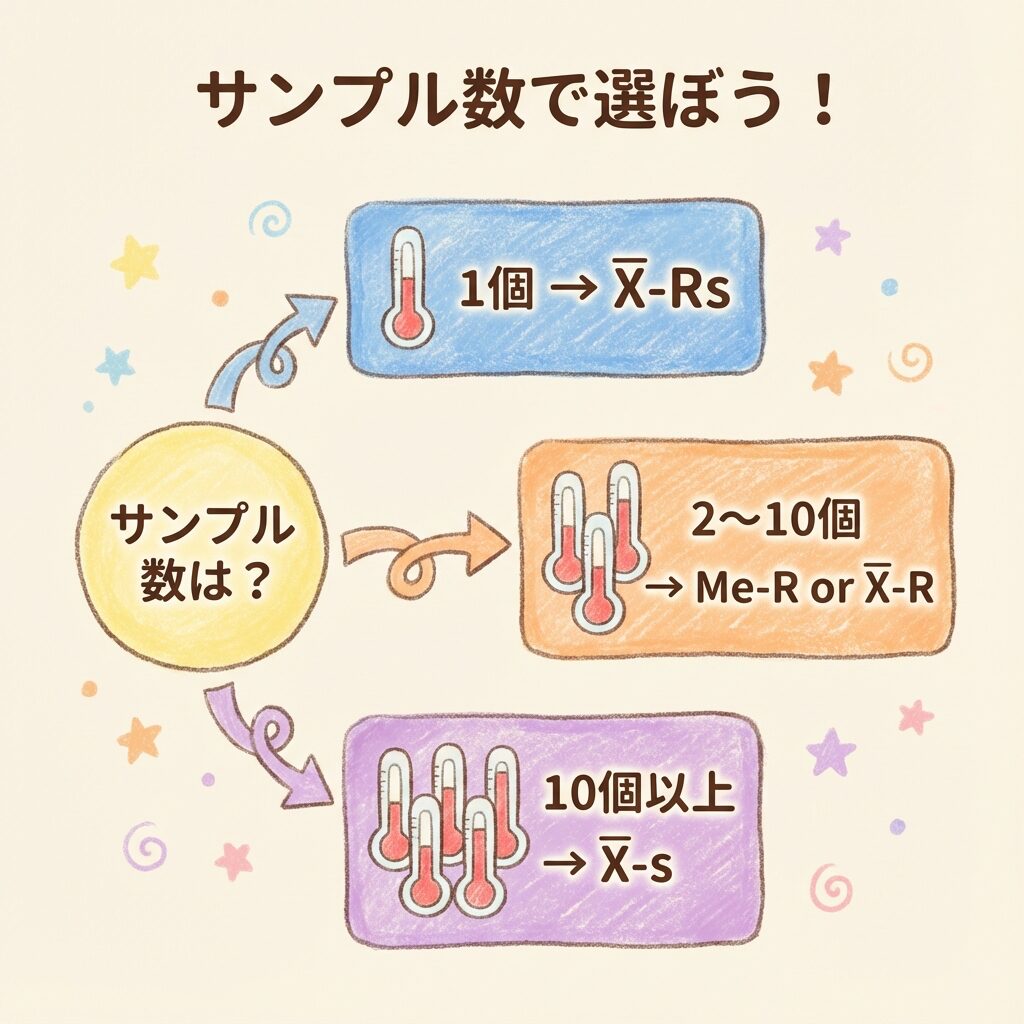
計量値(測れるデータ)の管理図は4種類あります。どれを使うかは、「サンプル数」と「計算の手間」で決まります。
📋 4つの管理図一覧
| 管理図 | 読み方 | サンプル数 | 特徴 |
|---|---|---|---|
| X̄-R | エックスバー・アール | 2〜10個 | 最も一般的 |
| X-Rs | エックス・アールエス | 1個 | データが1個ずつ |
| Me-R | メディアン・アール | 2〜10個 | 計算が簡単 |
| X̄-s | エックスバー・エス | 10個以上 | 精度が高い |
🔀 使い分けフローチャート
♨️ 温泉旅館でたとえると
あなたは温泉旅館「ゆらぎ荘」の支配人。お風呂の温度管理を任されています。
🌡️ X-Rs管理図
1時間に1回だけ温度を測る
→ データは1個ずつ
📊 Me-R管理図
3箇所で温度を測って「真ん中」を使う
→ 計算が楽
📈 X̄-s管理図
20箇所で温度を測って精密管理
→ 精度重視
💡 QC検定のポイント
「サンプルが1個 → X-Rs」「計算簡単 → Me-R」「大量データ → X̄-s」と覚えましょう!
🌡️ X-Rs管理図(個々の値−移動範囲管理図)
こんな時に使う!
✅ 1回に1個しかデータが取れないとき
✅ 化学プラントの温度・圧力など連続プロセス
✅ 検査に時間やコストがかかるとき
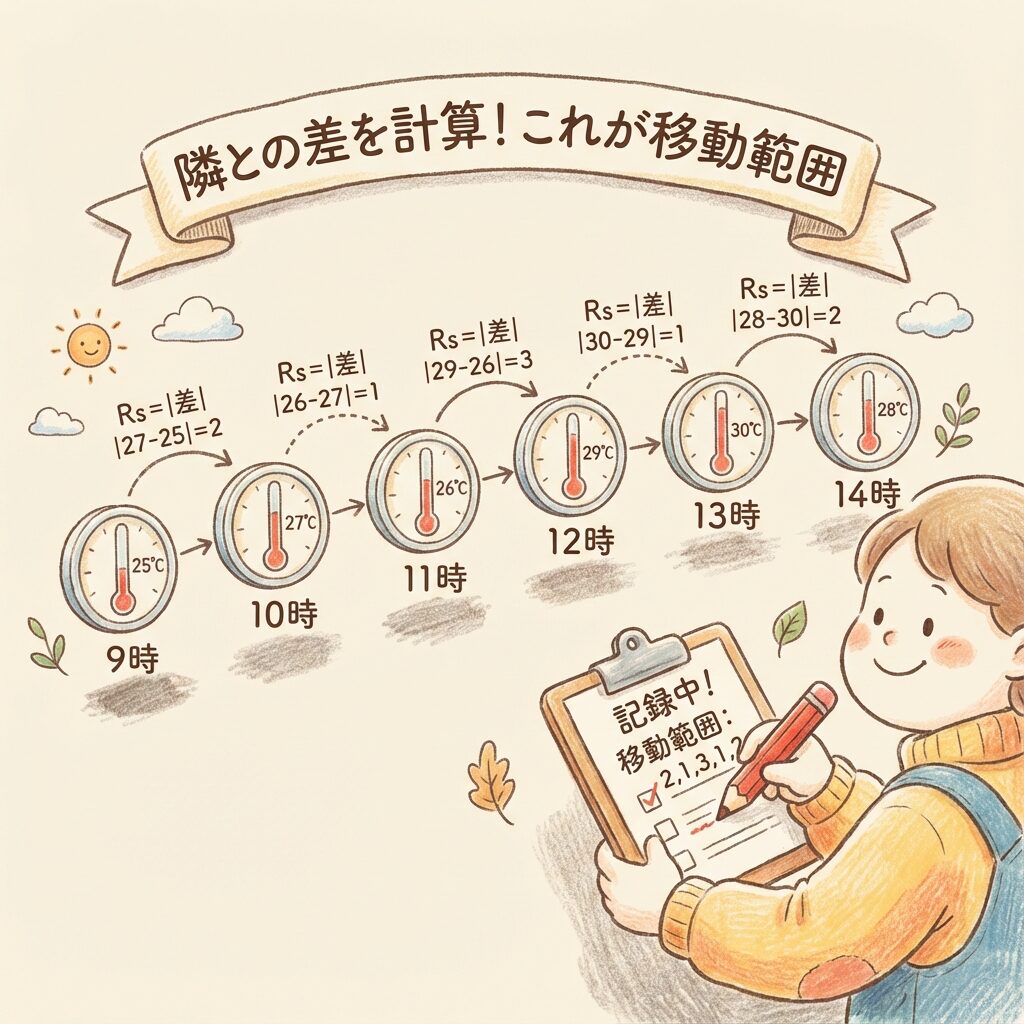
📝 X-Rsの「Rs」って何?
Rs = 移動範囲(Moving Range)のことです。
移動範囲の計算
Rs = |今回の値 − 前回の値|
「1個しかデータがないのにRなんて計算できるの?」と思いますよね。そこで、隣り合う2つのデータの差を使うのです!
📊 例題|温泉の温度データ
毎時間、露天風呂の温度を1回測定しました。
| 時刻 | 温度 X(℃) | 移動範囲 Rs |
|---|---|---|
| 9時 | 41 | − |
| 10時 | 42 | |42−41| = 1 |
| 11時 | 40 | |40−42| = 2 |
| 12時 | 41 | |41−40| = 1 |
| 13時 | 43 | |43−41| = 2 |
| 14時 | 42 | |42−43| = 1 |
| 平均 | X̄ = 41.5 | R̄s = 1.4 |
※ X̄ = (41+42+40+41+43+42)÷6 = 41.5 ※ R̄s = (1+2+1+2+1)÷5 = 1.4
📐 管理限界線の公式
X管理図
UCL = X̄ + 2.660 × R̄s
CL = X̄
LCL = X̄ − 2.660 × R̄s
Rs管理図
UCL = 3.267 × R̄s
CL = R̄s
LCL = なし
⚠️ 覚え方
X-Rs管理図の係数「2.660」と「3.267」は、n=2のX̄-R管理図と同じ!(隣り合う2つを使うから)
例題の計算
X管理図
UCL = 41.5 + 2.660 × 1.4 = 41.5 + 3.72 = 45.22℃
CL = 41.50℃
LCL = 41.5 − 2.660 × 1.4 = 41.5 − 3.72 = 37.78℃
Rs管理図
UCL = 3.267 × 1.4 = 4.57
CL = 1.40
LCL = なし
📊 Me-R管理図(メディアン−範囲管理図)
こんな時に使う!
✅ 現場で電卓なしでサッと計算したいとき
✅ 作業者が計算が苦手でも使えるようにしたいとき
✅ X̄-R管理図と同程度の精度でOKなとき
📝 Me(メディアン)って何?
Me = 中央値のことです。データを小さい順に並べたとき、真ん中にくる値です。
メディアンの見つけ方
データ:40, 42, 41 → 並べ替え:40, 41, 42 → Me = 41
※ 足し算・割り算なし!並べて真ん中を見るだけ!
⚠️ 注意
サンプル数が奇数のとき使います(3個、5個、7個など)。偶数だと「真ん中」が2つになって計算が必要になるため、Me-Rの利点が薄れます。
📊 例題|内湯の温度データ(n=3)
内湯の3箇所(左端・中央・右端)で温度を測定しました。
| 日 | 左端 | 中央 | 右端 | Me | R |
|---|---|---|---|---|---|
| 1日目 | 40 | 42 | 41 | 41 | 2 |
| 2日目 | 41 | 40 | 42 | 41 | 2 |
| 3日目 | 39 | 41 | 43 | 41 | 4 |
| 4日目 | 42 | 41 | 40 | 41 | 2 |
| 5日目 | 40 | 40 | 42 | 40 | 2 |
| 平均 | − | M̃e = 40.8 | R̄ = 2.4 | ||
📐 管理限界線の公式
Me管理図
UCL = M̃e + A₄ × R̄
CL = M̃e
LCL = M̃e − A₄ × R̄
R管理図
UCL = D₄ × R̄
CL = R̄
LCL = D₃ × R̄(n≦6は「なし」)
係数表(Me-R用)
| n | A₄ | D₃ | D₄ |
|---|---|---|---|
| 3 | 1.187 | − | 2.575 |
| 5 | 0.691 | − | 2.115 |
| 7 | 0.509 | 0.076 | 1.924 |
例題の計算(n=3)
Me管理図
UCL = 40.8 + 1.187 × 2.4 = 40.8 + 2.85 = 43.65℃
CL = 40.80℃
LCL = 40.8 − 1.187 × 2.4 = 40.8 − 2.85 = 37.95℃
R管理図
UCL = 2.575 × 2.4 = 6.18
CL = 2.40
LCL = なし

📈 X̄-s管理図(平均−標準偏差管理図)
こんな時に使う!
✅ サンプル数が10個以上と多いとき
✅ 高精度な管理が必要なとき
✅ コンピュータで自動計算できる環境
📝 「s」って何?
s = 標準偏差(Standard Deviation)のことです。「データがどれくらいバラついているか」を数値で表します。
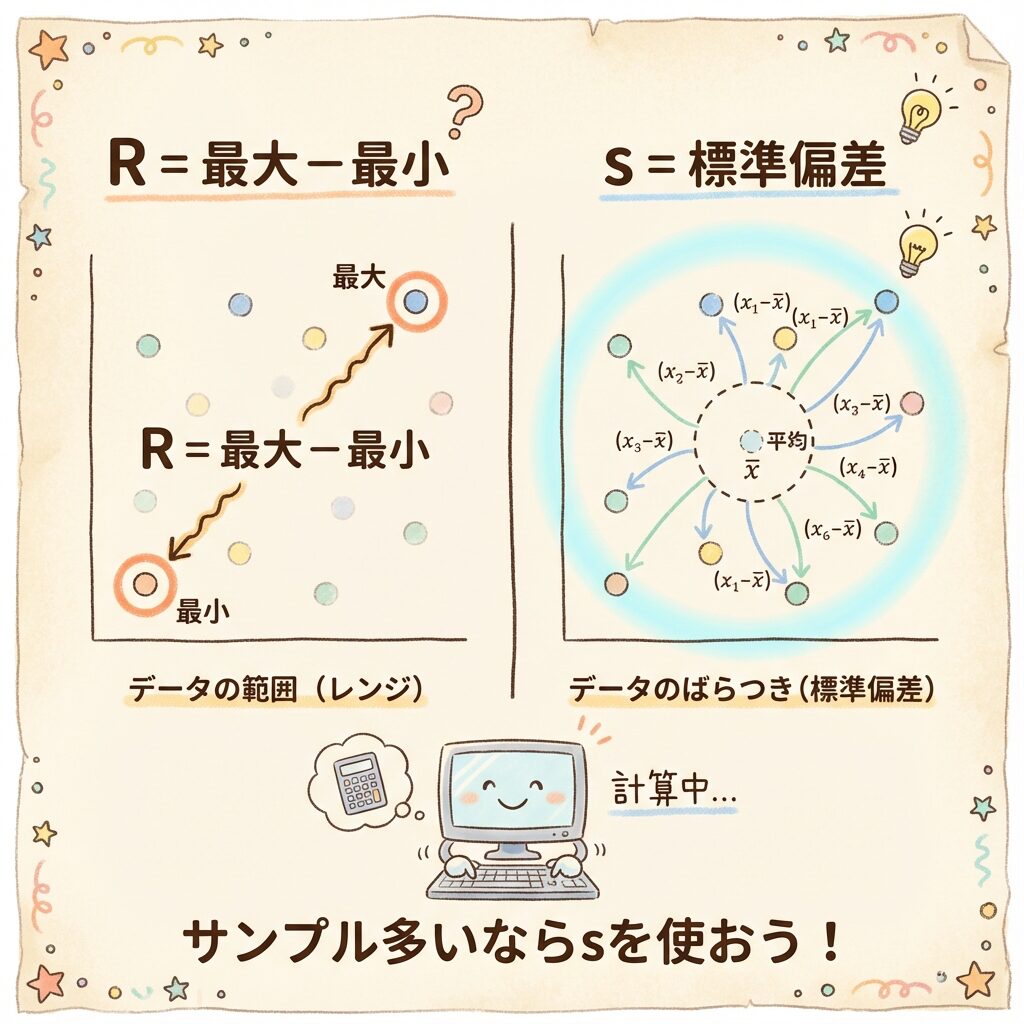
RとSの違い
R(範囲):最大 − 最小 → 計算カンタン、ざっくり
s(標準偏差):すべてのデータから計算 → 計算は大変、精度高い
🔢 なぜサンプル10個以上で使う?
Rは「最大と最小」の2つしか使いません。だからサンプルが多いと、途中のデータが無視されるんです。
例:10個のデータ
38, 39, 40, 40, 41, 41, 41, 42, 42, 45
R = 45 − 38 = 7(途中の8個は無視!)
s = すべてのデータから計算 → より正確にバラつきがわかる
📐 管理限界線の公式
X̄管理図
UCL = X̿ + A₃ × s̄
CL = X̿
LCL = X̿ − A₃ × s̄
s管理図
UCL = B₄ × s̄
CL = s̄
LCL = B₃ × s̄
係数表(X̄-s用)
| n | A₃ | B₃ | B₄ |
|---|---|---|---|
| 10 | 0.975 | 0.284 | 1.716 |
| 15 | 0.789 | 0.428 | 1.572 |
| 20 | 0.680 | 0.510 | 1.490 |
| 25 | 0.606 | 0.565 | 1.435 |
例題の計算(n=10)
X̿ = 41.0、s̄ = 1.5 のとき
X̄管理図
UCL = 41.0 + 0.975 × 1.5 = 41.0 + 1.46 = 42.46℃
CL = 41.00℃
LCL = 41.0 − 0.975 × 1.5 = 41.0 − 1.46 = 39.54℃
s管理図
UCL = 1.716 × 1.5 = 2.57
CL = 1.50
LCL = 0.284 × 1.5 = 0.43
💡 X̄-sの特徴
s管理図はLCLがある(ゼロではない)のが特徴!バラつきが小さすぎても異常と判定されます。
📊 4つの管理図 比較まとめ
| 項目 | X̄-R | X-Rs | Me-R | X̄-s |
|---|---|---|---|---|
| サンプル数 | 2〜10 | 1 | 2〜10(奇数) | 10以上 |
| 計算の手間 | 普通 | 簡単 | 最も簡単 | 大変 |
| 精度 | 高い | やや低い | 普通 | 最も高い |
| 係数 | A₂, D₃, D₄ | 2.660, 3.267 | A₄, D₃, D₄ | A₃, B₃, B₄ |
| 下限LCL | R: n≦6でなし | Rs: なし | R: n≦6でなし | s: あり |
🎯 QC検定でよく出る問題
パターン①:X-Rsの移動範囲を求める
【問題】
連続する測定値が 25, 27, 24, 26 のとき、3番目の移動範囲Rs₃を求めよ。
【解答】
Rs₃ = |24 − 27| = 3
※ 3番目と2番目の差を取る
パターン②:Me-Rのメディアンを求める
【問題】
あるグループの測定値が 52, 48, 50, 51, 49(n=5)のとき、メディアンMeを求めよ。
【解答】
小さい順:48, 49, 50, 51, 52
真ん中の値 → Me = 50
パターン③:どの管理図を使うか
【問題】
化学プラントで1時間に1回だけ温度を測定する。適切な管理図は?
【解答】
サンプルが1個ずつ → X-Rs管理図
【問題】
各グループでサンプルを20個ずつ取得できる。最も精度の高い管理図は?
【解答】
サンプルが10個以上で精度重視 → X̄-s管理図
✨ 係数の覚え方まとめ
X̄-R:A₂(エーツー)、D₃・D₄(ディー)
X-Rs:2.660と3.267(n=2と同じ)
Me-R:A₄(エーフォー)、D₃・D₄
X̄-s:A₃(エースリー)、B₃・B₄(ビー)
🔗 関連記事
管理図の異常判定ルール8つはこちらの記事で詳しく解説しています。
📝 この記事のまとめ
✨ 3つの管理図をマスターしました!
🌡️ X-Rs管理図
サンプル1個のとき。移動範囲Rs = |今回 − 前回|
📊 Me-R管理図
計算を簡単に。メディアンMe = 並べて真ん中
📈 X̄-s管理図
サンプル10個以上で高精度。標準偏差sを使用
🔑 選び方のコツ
「サンプル数」→「計算の手間」→「精度」の順で考えよう!
🗺️ シリーズ記事一覧
① 全体像
管理図と工程能力指数の完全ロードマップ② 超入門
品質管理の"バラつき"って何?③ 基礎
管理図とは?UCL・CL・LCLの意味④ 種類
管理図の種類一覧と選び方⑤ 判定
管理図の異常判定ルール8つ⑥ 活用
管理図の読み方|異常を見つけたら?⑦ 計量値①
X̄-R管理図の作り方⑧ 今ここ!
X-Rs・Me-R・X̄-s管理図の計算方法
⑨ 計数値①
np管理図・p管理図の作り方⑩ 計数値②
c管理図・u管理図の作り方⑪ 工程能力①
工程能力指数Cp・Cpkとは?⑫ 工程能力②
工程能力指数の判定基準🎉 お疲れ様でした!
計量値の管理図は完全マスター!
次は計数値の管理図(np・p管理図)に進みましょう。
