📏 この記事を読んでいるあなたへ
「CpとCpk、何が違うの?」
「計算式を見ても、意味がわからない…」
「なぜ2つの指数が必要なの?」
大丈夫です。この記事では、ペットボトル工場の容量検査を例に、CpとCpkの違いと計算方法を図解でわかりやすく解説します!
目次
🎯 この記事でわかること
✅ 工程能力指数とは何か
✅ CpとCpkの違い(図解で理解)
✅ それぞれの計算方法と公式
✅ 例題を使った実践的な計算
✅ QC検定でよく出る問題パターン
📍 シリーズ全体像|今ここ!
管理図シリーズ(全12記事)
① ロードマップ → ② バラつき入門 → ③ 管理図とは → ④ 種類一覧 → ⑤ 異常判定ルール → ⑥ 読み方・活用法 → ⑦ X̄-R管理図 → ⑧ その他計量値 → ⑨ np・p管理図 → ⑩ c・u管理図
⑪ 工程能力指数Cp・Cpk ← 今ここ!
→ ⑫ 判定基準
💡 管理図との関係
管理図で「工程が安定しているか」を確認した後、工程能力指数で「規格を満たす実力があるか」を評価します。管理図の基本を先に読んでおくと理解が深まります!

🏭 工程能力指数って何?
一言でいうと「規格に対する工程の実力」を数値化したもの
工程能力指数は、「この工程で作った製品が、どれくらい規格内に収まるか」を表す数値です。
🍶 ペットボトル工場でたとえると
あなたはペットボトル飲料工場の品質管理担当。500mlのお茶を製造しています。
📋 規格(スペック)
上限規格(USL):510ml(これ以上は入れすぎ)
下限規格(LSL):490ml(これ以下は少なすぎ)
目標:500ml ぴったり
工程能力指数は「490ml〜510mlの範囲に、どれくらい余裕を持って収まっているか」を数値で表します。
📝 用語を整理しよう
| 用語 | 記号 | 意味 |
|---|---|---|
| 上限規格 | USL | Upper Spec Limit(上限値) |
| 下限規格 | LSL | Lower Spec Limit(下限値) |
| 平均値 | X̄(μ) | データの中心 |
| 標準偏差 | σ(s) | データのバラつき具合 |
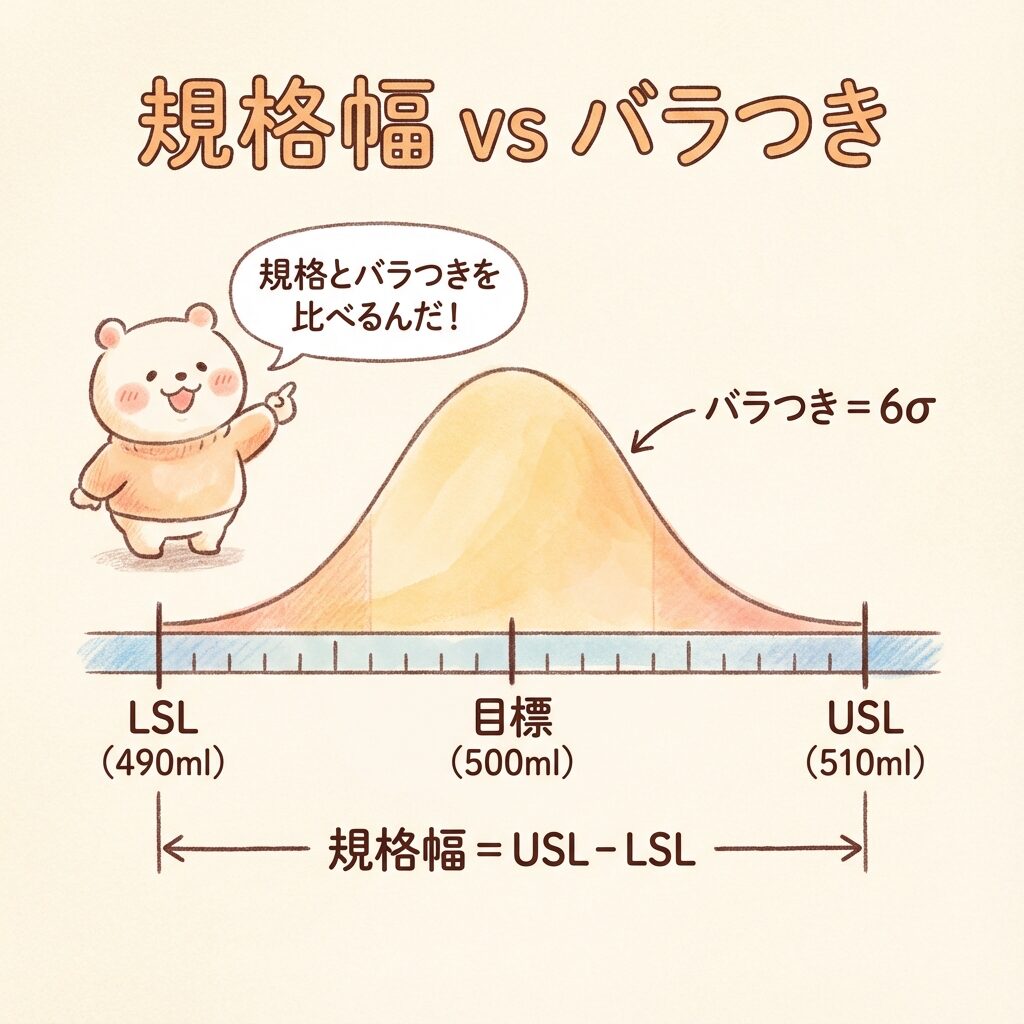
| 規格幅 | USL−LSL | 規格の上限と下限の差 |
💡 ポイント
工程能力指数は「規格幅」と「バラつき(6σ)」を比較します。
バラつきが小さいほど、規格内に余裕を持って収まります!
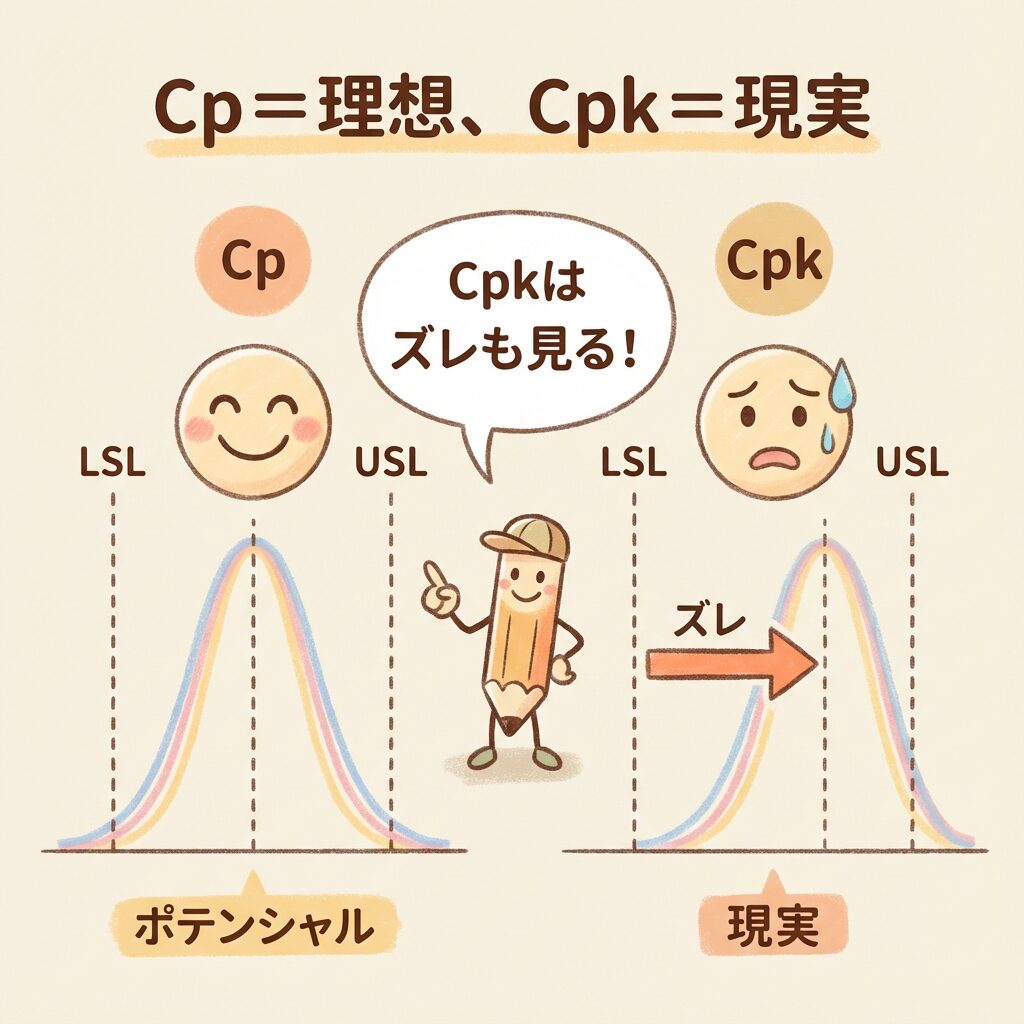
⚖️ CpとCpkの違い(超重要!)
結論から言うと、平均値のズレを考慮するかどうかの違いです。
Cp
潜在的な工程能力
意味:
「もし平均が中心にあったら」
どれくらいの能力があるか
※ 平均のズレは無視
Cpk
実際の工程能力
意味:
平均のズレも含めた
現実の能力
※ 平均のズレを考慮
🎯 図で理解しよう!
ケース①:平均が中心にある場合
LSL ──────┃──────── USL
∧
/ \
/ \
───/─────────\───
平均 = 規格の中心 → Cp = Cpk
両方同じ値になる!
ケース②:平均がズレている場合
LSL ──────┃──────── USL
∧
/ \
/ \
─────────/─────────\
平均が右にズレ → Cpk < Cp
Cpkは小さくなる!
🍶 ペットボトルでたとえると
📏 Cp(潜在能力)
「このラインのバラつきなら、中心を500mlに合わせれば規格内に収まるよね」
→ バラつきだけを見た「ポテンシャル」
🎯 Cpk(実際の能力)
「実際は平均が505mlにズレてるから、上限510mlに近くて危ない」
→ ズレも含めた「現実の実力」
⚠️ 超重要!
Cpk ≦ Cp が必ず成り立ちます。
平均が中心からズレるほど、Cpkは小さくなります。
だから実務ではCpkを重視します!
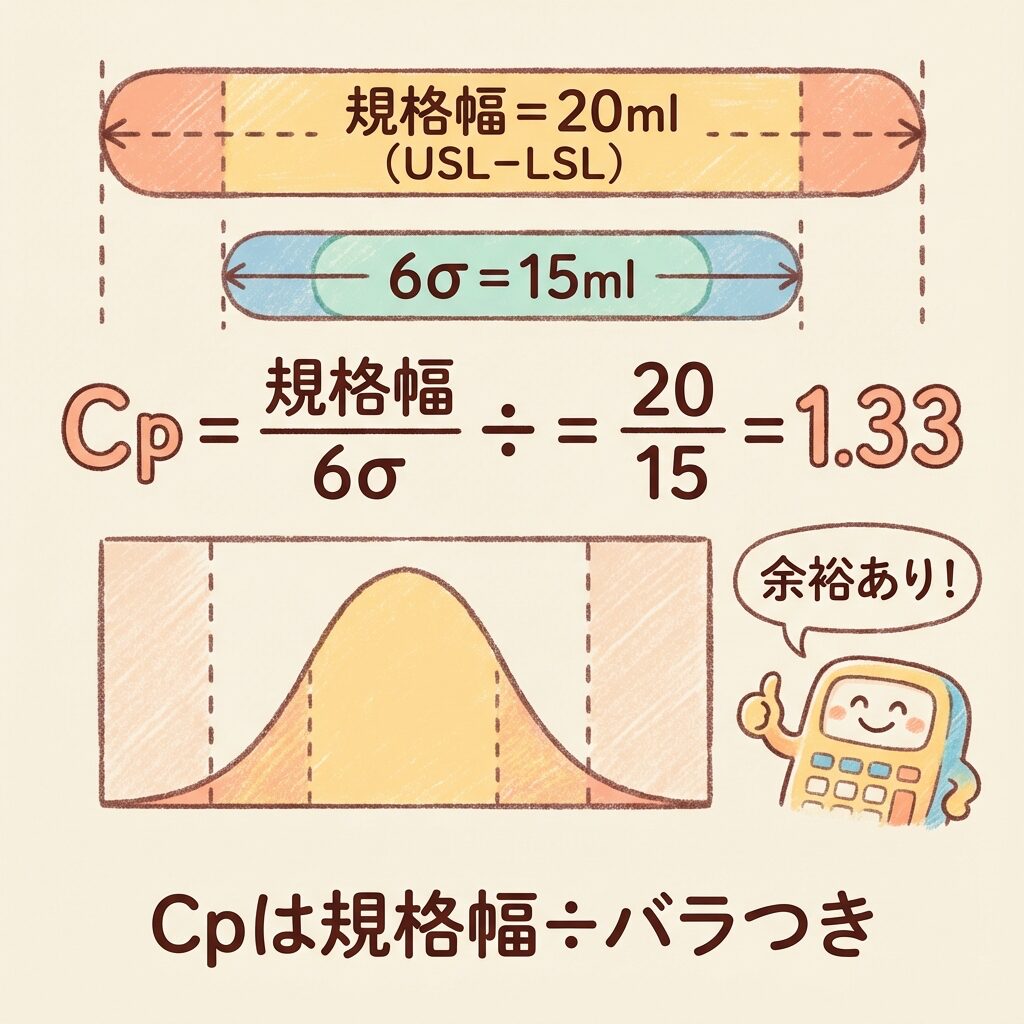
📐 Cpの計算方法
公式(シンプル!)
Cp = (USL − LSL) ÷ 6σ
意味を分解すると:
分子(USL − LSL):規格幅(許容される範囲)
分母(6σ):工程のバラつき幅(±3σの範囲)
→「規格幅」が「バラつき幅」の何倍あるか?
🤔 なぜ6σ?
正規分布では、平均 ± 3σ の範囲に99.73%のデータが入るとされています。
つまり、−3σ から +3σ までの幅 = 6σ
この「6σ」を「工程の実質的なバラつき幅」として使います。
📝 例題|ペットボトルの容量
【条件】
・上限規格(USL)= 510ml
・下限規格(LSL)= 490ml
・標準偏差(σ)= 2.5ml
・平均(X̄)= 500ml(中心にある)
【計算】
① 規格幅を計算
USL − LSL = 510 − 490 = 20ml
② 6σを計算
6σ = 6 × 2.5 = 15ml
③ Cpを計算
Cp = 20 ÷ 15 = 1.33
💡 解釈
Cp = 1.33 は「規格幅がバラつき幅の1.33倍ある」という意味。
つまり、バラつきに対して規格に余裕がある状態です!
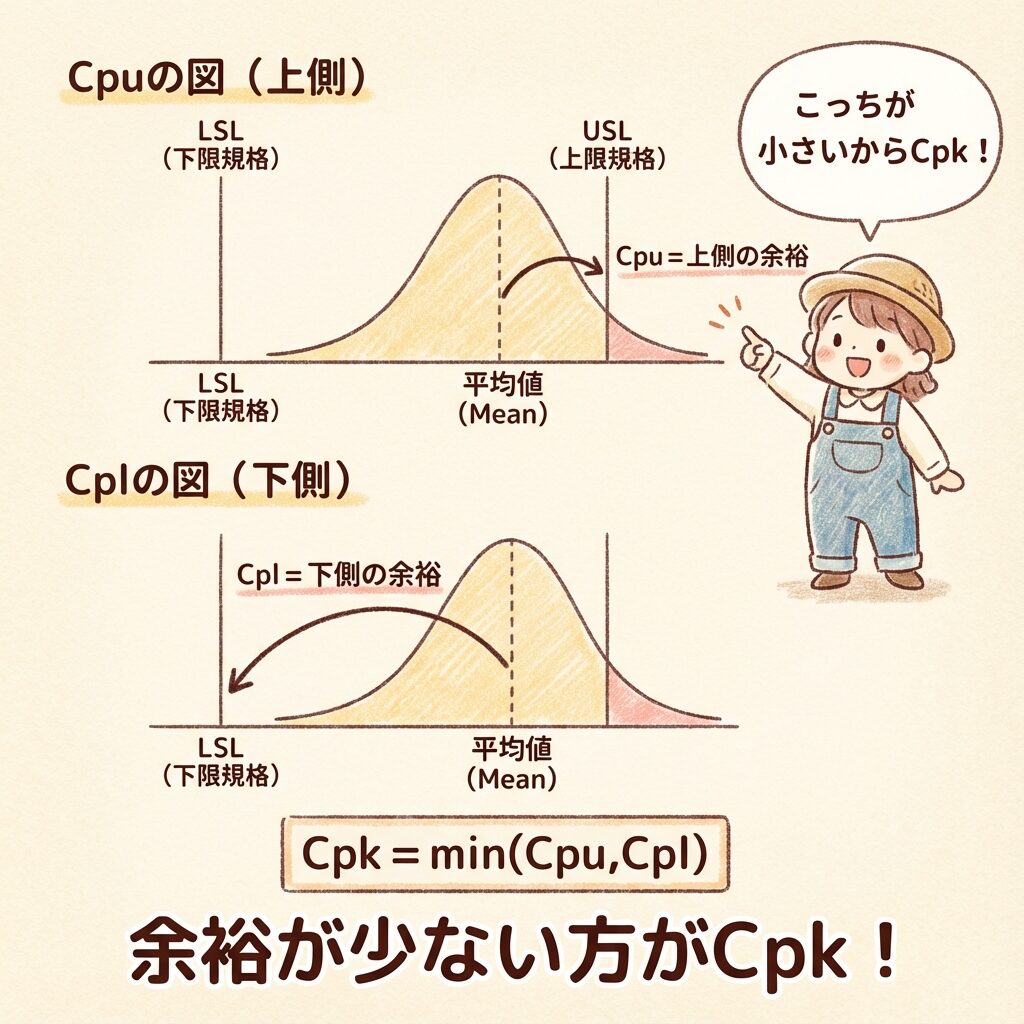
🎯 Cpkの計算方法
公式(2つの値の小さい方!)
Cpk = min(Cpu, Cpl)
Cpu = (USL − X̄) ÷ 3σ ←上側の余裕
Cpl = (X̄ − LSL) ÷ 3σ ←下側の余裕
意味を分解すると:
Cpu:平均から上限規格までの余裕(上に何σ分あるか)
Cpl:平均から下限規格までの余裕(下に何σ分あるか)
→ 余裕が少ない方がCpkになる!
💡 なぜ「小さい方」?
チェーンの強さは「一番弱い部分」で決まりますよね。
同じように、工程能力は「規格に近い方(余裕が少ない方)」で決まります!
📝 例題①|平均が中心にある場合
【条件】
・USL = 510ml、LSL = 490ml
・σ = 2.5ml
・X̄ = 500ml(中心にある)
【計算】
① Cpu(上側の余裕)
Cpu = (510 − 500) ÷ (3 × 2.5) = 10 ÷ 7.5 = 1.33
② Cpl(下側の余裕)
Cpl = (500 − 490) ÷ (3 × 2.5) = 10 ÷ 7.5 = 1.33
③ Cpk(小さい方を選ぶ)
Cpk = min(1.33, 1.33) = 1.33
平均が中心にあるので、Cp = Cpk = 1.33 になりました!
📝 例題②|平均がズレている場合
【条件】
・USL = 510ml、LSL = 490ml
・σ = 2.5ml
・X̄ = 505ml(上にズレている!)
【計算】
① Cpu(上側の余裕)
Cpu = (510 − 505) ÷ 7.5 = 5 ÷ 7.5 = 0.67 ←少ない!
② Cpl(下側の余裕)
Cpl = (505 − 490) ÷ 7.5 = 15 ÷ 7.5 = 2.00 ←余裕あり
③ Cpk(小さい方を選ぶ)
Cpk = min(0.67, 2.00) = 0.67
⚠️ 注目!
Cp = 1.33(バラつき自体は同じ)
Cpk = 0.67(平均がズレたから下がった)
同じバラつきでも、平均がズレるとCpkは大きく下がる!
だから実務ではCpkを見ることが重要なのです。
📊 Cp vs Cpk 比較まとめ
| 項目 | Cp | Cpk |
|---|---|---|
| 正式名称 | 工程能力指数 | 片側工程能力指数 |
| 意味 | 潜在的な能力 | 実際の能力 |
| 平均のズレ | 考慮しない | 考慮する |
| 公式 | (USL−LSL)÷6σ | min(Cpu, Cpl) |
| 関係 | Cpk ≦ Cp(常に成り立つ) | |
| 実務での重要度 | 参考値 | より重要! |
🎯 QC検定でよく出る問題
パターン①:Cpを求めよ
【問題】
USL = 55、LSL = 45、σ = 1.5 のとき、Cpを求めよ。
【解答】
規格幅 = 55 − 45 = 10
6σ = 6 × 1.5 = 9
Cp = 10 ÷ 9 = 1.11
パターン②:Cpkを求めよ
【問題】
USL = 55、LSL = 45、σ = 1.5、X̄ = 52 のとき、Cpkを求めよ。
【解答】
3σ = 3 × 1.5 = 4.5
Cpu = (55 − 52) ÷ 4.5 = 3 ÷ 4.5 = 0.67
Cpl = (52 − 45) ÷ 4.5 = 7 ÷ 4.5 = 1.56
Cpk = min(0.67, 1.56) = 0.67
パターン③:CpとCpkの関係を問う
【問題】
Cp = 1.5、Cpk = 1.2 のとき、工程について言えることは?
【解答】
Cp > Cpk なので、平均が規格の中心からズレている
→ 平均を中心に調整すれば、Cpk = Cp = 1.5 にできる可能性がある
パターン④:片側規格の場合
【問題】
上限規格のみ USL = 100、X̄ = 94、σ = 2 のとき、工程能力指数を求めよ。
【解答】
片側規格なので Cpu のみ計算
Cpu = (100 − 94) ÷ (3 × 2) = 6 ÷ 6 = 1.00
💡 片側規格のポイント
上限のみ → Cpu を使う
下限のみ → Cpl を使う
両側規格 → Cpk = min(Cpu, Cpl)
🔗 関連記事
工程能力指数の判定基準(1.67, 1.33, 1.00, 0.67の意味)は次の記事で詳しく解説しています。

📝 公式まとめ(試験直前チェック用)
📐 Cp(潜在能力)
Cp = (USL − LSL) ÷ 6σ
※ 平均のズレは無視
🎯 Cpk(実際の能力)
Cpk = min(Cpu, Cpl)
Cpu = (USL − X̄) ÷ 3σ
Cpl = (X̄ − LSL) ÷ 3σ
※ 平均のズレを考慮
✨ この記事のまとめ
✅ 工程能力指数:規格に対する工程の実力を数値化
✅ Cp:「バラつきだけ」を見た潜在能力
✅ Cpk:「バラつき+ズレ」を見た実際の能力
✅ 関係:Cpk ≦ Cp(平均がズレるとCpkが下がる)
✅ 実務:Cpkをより重視する
🧠 覚え方のコツ
Cp:「Capability(能力)」のポテンシャル
Cpk:「k」は「かたより(偏り)」を考慮
→ kが付くと「より現実的」と覚えよう!
🗺️ シリーズ記事一覧
① 全体像
管理図と工程能力指数の完全ロードマップ② 超入門
品質管理の"バラつき"って何?③ 基礎
管理図とは?UCL・CL・LCLの意味④ 種類
管理図の種類一覧と選び方⑤ 判定
管理図の異常判定ルール8つ⑥ 活用
管理図の読み方|異常を見つけたら?⑦ 計量値①
X̄-R管理図の作り方⑧ 計量値②
X-Rs・Me-R・X̄-s管理図の計算方法⑨ 計数値①
np管理図・p管理図の作り方⑩ 計数値②
c管理図・u管理図の作り方⑪ 今ここ!
工程能力指数Cp・Cpkとは?
⑫ 工程能力②
工程能力指数の判定基準🎉 シリーズ完結まであと1記事!
次は最終回!工程能力指数の判定基準を学びましょう。
「Cp = 1.33って良いの?悪いの?」の疑問を解決します!

統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


