- 「分散を計算するとき、なぜnではなくn-1で割るの?」
- 「自由度って何?名前からして意味が分からない」
- 「t検定やF検定で出てくる自由度、どう計算すればいいの?」
- 「分散分析表の自由度の欄、何を書けばいいか分からない」
自由度とは「自由に決められるデータの個数」のことです。
5人のテストの点数があっても、「平均が60点」と決まった瞬間、最後の1人の点数は自動的に決まってしまいます。だから自由度は「5-1=4」。この記事では、この感覚を「4人席のテーブル」のたとえで完全に理解できるように解説します。
統計学を学んでいると、必ず出てくるのが「自由度」という言葉。
分散の計算で「n-1で割る」と習ったとき、「なぜ?」と思いませんでしたか?
t検定の問題で「自由度を求めよ」と言われて、困ったことはありませんか?
実は、自由度の本質はとてもシンプルです。
「1つの条件が決まると、1つの自由が奪われる」
これだけ覚えておけば、どんな場面でも自由度を正しく計算できます。
- 自由度の直感的なイメージ
- なぜ分散はn-1で割るのか
- t検定・F検定での自由度の計算方法
- 分散分析表での自由度の求め方
目次
🪑 自由度とは?「4人席のテーブル」で理解する
自由度を理解するために、レストランの「4人席のテーブル」をイメージしてください。
あなたは友達3人と、合計4人でレストランに行きました。
4人席のテーブルに案内されます。
最初の3人は、好きな席に座れます。
「窓際がいい」「通路側がいい」と自由に選べます。
でも最後の1人は?
残った1席に座るしかありません。選ぶ自由がないのです。
これが「自由度」の本質です。
自由度 = 全体の数 − 制約(縛り)の数
4人席のテーブルで、4人全員が座らなければならない(制約=1)
→ 自由度 = 4 − 1 = 3
🔢 数学的に考えてみよう
もう少し数学的に考えてみましょう。
5つの数字があり、その合計が100と決まっているとします。
□ + □ + □ + □ + □ = 100
最初の4つは自由に決められます。
20 + 15 + 30 + 25 + □ = 100
でも、最後の1つは?
20 + 15 + 30 + 25 = 90 なので、最後は必ず10になります。
20 + 15 + 30 + 25 + 10 = 100
↑ この数字は自動的に決まる(自由がない)
5つの数字があっても、「合計=100」という制約(縛り)が1つあるため、自由に決められるのは4つだけ。
自由度 = 5 − 1 = 4

📊 なぜ分散は「n-1」で割るのか?
ここからが本題です。
分散を計算するとき、なぜnではなくn-1で割るのでしょうか?
まず、分散の計算式を確認しましょう。
標本分散(不偏分散)
s² = Σ(xᵢ − x̄)² ÷ (n − 1)
x̄ は標本平均、n はデータの個数
この「n-1」の正体は、まさに自由度です。
🤔 なぜ「-1」されるのか?
分散を計算するとき、私たちは平均値(x̄)を先に計算します。
この瞬間、1つの制約が生まれます。
5人のテストの点数があります。
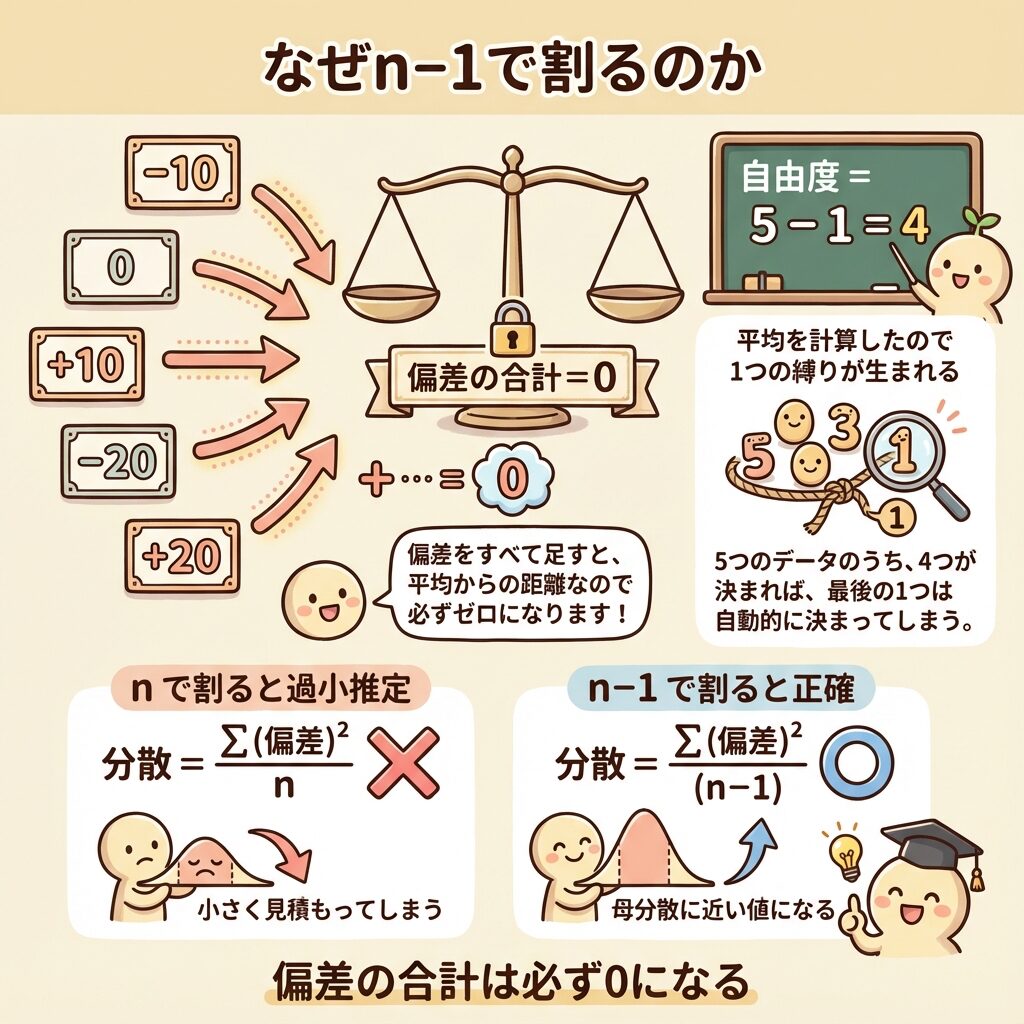
60, 70, 80, 50, 90(平均 = 70点)
それぞれの「偏差」(平均からのズレ)を計算すると…
-10, 0, +10, -20, +20
偏差の合計は必ず0になります。
(-10 + 0 + 10 - 20 + 20 = 0)
偏差の合計が0になるということは、最後の1つの偏差は、他の偏差から自動的に決まるということです。
4つの偏差が決まれば、5つ目は「合計が0になるように」決まってしまう。
だから、自由に動けるデータは n-1 個なのです。
もし n で割ってしまうと、分散が小さく計算されてしまいます。
なぜなら、自由に動けないデータまで「自由に動ける」と仮定してしまうから。
これを「過小推定」と呼びます。
n-1 で割ることで、この過小推定を補正しているのです。
分散と標準偏差の基礎をもっと詳しく知りたい方はこちら。
👉 第5回:分散と標準偏差|「バラつき」を数値化する魔法の公式
📝 具体例で確認しよう
実際に計算してみましょう。
データ:60, 70, 80, 50, 90(n = 5)
ステップ1:平均を求める
x̄ = (60 + 70 + 80 + 50 + 90) ÷ 5 = 350 ÷ 5 = 70
ステップ2:偏差を求める
60 - 70 = -10
70 - 70 = 0
80 - 70 = +10
50 - 70 = -20
90 - 70 = +20
ステップ3:偏差の2乗の合計を求める
(-10)² + 0² + 10² + (-20)² + 20²
= 100 + 0 + 100 + 400 + 400 = 1000
ステップ4:自由度(n-1)で割る
s² = 1000 ÷ (5 - 1) = 1000 ÷ 4 = 250
・データの個数:n = 5
・制約の数:1(平均を計算したから)
・自由度:n - 1 = 4
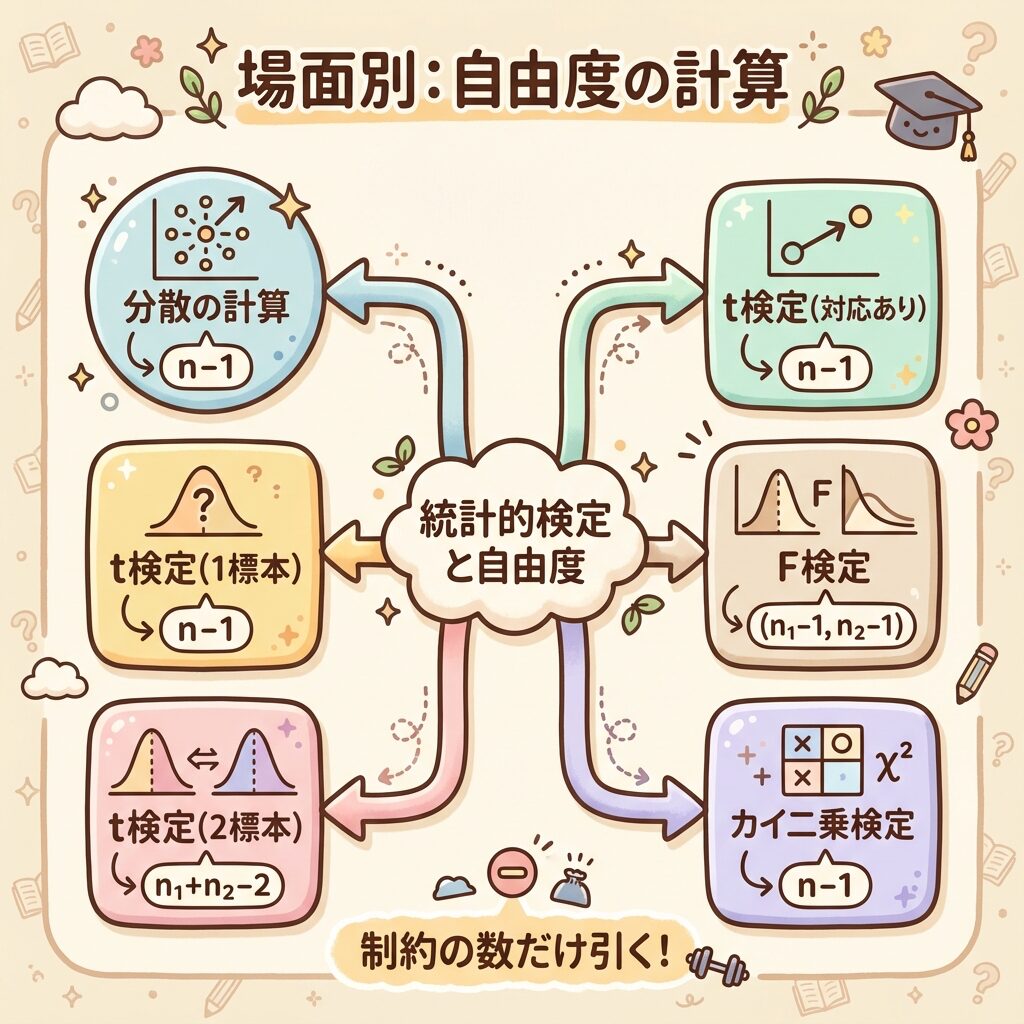
📋 場面別:自由度の計算方法
自由度は、統計学のあらゆる場面で登場します。
ここでは、代表的な場面での自由度の計算方法をまとめます。
📊 場面①:分散の計算
自由度 = n − 1
n = データの個数
制約 = 平均を1つ計算したから「-1」
📊 場面②:t検定(1標本)
「このサンプルの平均は、母平均と違うか?」を調べるt検定です。
自由度 = n − 1
分散の計算と同じ理由で「-1」
t検定の詳しい解説はこちら。
👉 t検定(母分散未知・一標本)「この部品の長さは規格通り?」
📊 場面③:t検定(2標本・対応なし)
「AグループとBグループの平均に差があるか?」を調べるt検定です。
自由度 = n₁ + n₂ − 2
n₁ = Aグループのデータ数
n₂ = Bグループのデータ数
制約 = 2つのグループそれぞれで平均を計算したから「-2」
Aグループ:10人のデータ
Bグループ:15人のデータ
自由度 = 10 + 15 - 2 = 23
2標本t検定の詳しい解説はこちら。
👉 t検定(2標本・等分散)「スチューデントのt検定」でAとBの差を証明する手順
📊 場面④:t検定(対応あり)
「ダイエット前後で体重に差があるか?」のように、同じ人の前後を比較するt検定です。
自由度 = n − 1
n = ペアの数(人数)
「差」のデータを1つの変数として扱うので、1標本t検定と同じ
対応のあるt検定の詳しい解説はこちら。
👉 対応のあるt検定「ダイエットで痩せた?」個人差を消して差を見抜く最強の手法
📊 場面⑤:F検定(等分散の検定)
「2つのグループのバラつきは同じか?」を調べるF検定です。
第1自由度 = n₁ − 1
第2自由度 = n₂ − 1
F検定では「2つの自由度」が必要
分子の自由度(第1)と分母の自由度(第2)
F検定の詳しい解説はこちら。
👉 F検定(等分散の検定)「A機とB機、精度が良いのはどっち?」
📊 場面⑥:カイ二乗検定(母分散の検定)
「このデータのバラつきは、基準値と同じか?」を調べる検定です。
自由度 = n − 1
カイ二乗検定の詳しい解説はこちら。
👉 カイ二乗検定(母分散)「この機械、バラつき増えてない?」を1つのデータで検証
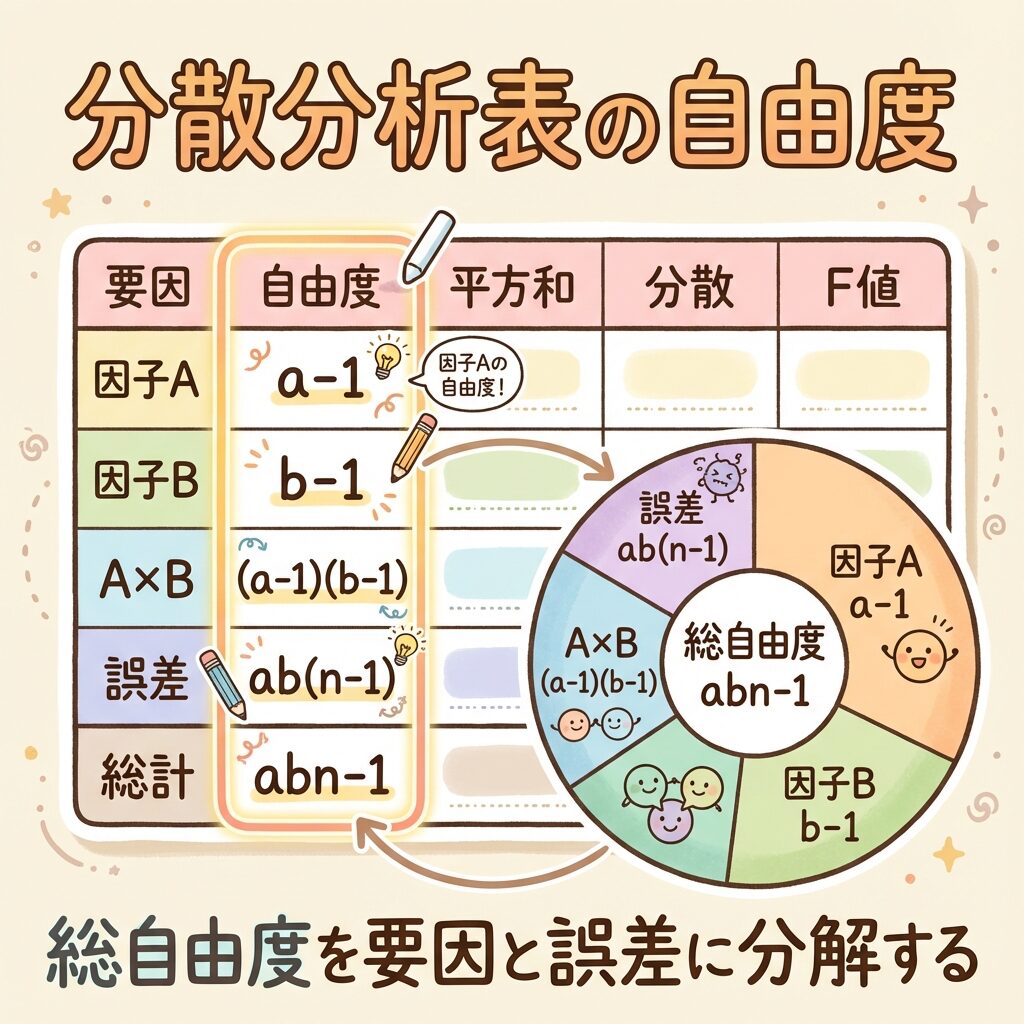
📈 分散分析(ANOVA)での自由度
実験計画法やQC検定で最も重要なのが、分散分析表での自由度です。
分散分析では、「総自由度」を「要因の自由度」と「誤差の自由度」に分解します。
📊 一元配置実験の場合
| 要因 | 自由度の公式 | 意味 |
|---|---|---|
| 因子A | a − 1 | 水準数 − 1 |
| 誤差 | a(n − 1) | 各水準内の自由度の合計 |
| 総計 | an − 1 | 総データ数 − 1 |
a = 水準数、n = 各水準の繰返し数
a = 3(水準数)
n = 5(繰返し数)
総データ数 = 3 × 5 = 15
因子Aの自由度 = 3 − 1 = 2
誤差の自由度 = 3 × (5 − 1) = 3 × 4 = 12
総自由度 = 15 − 1 = 14
確認:2 + 12 = 14 ✓
📊 二元配置実験(繰返しあり)の場合
| 要因 | 自由度の公式 |
|---|---|
| 因子A | a − 1 |
| 因子B | b − 1 |
| 交互作用 A×B | (a − 1)(b − 1) |
| 誤差 | ab(n − 1) |
| 総計 | abn − 1 |
a = Aの水準数、b = Bの水準数、n = 繰返し数
自由度の計算で迷ったら、この原則を思い出してください。
「水準数から1を引く」
・因子Aが3水準 → 自由度 = 3 - 1 = 2
・因子Bが2水準 → 自由度 = 2 - 1 = 1
・交互作用 → それぞれの自由度を掛ける = 2 × 1 = 2
分散分析表の作り方を完全図解した記事はこちら。
👉 【実験計画法】分散分析表の作り方完全ガイド
一元配置実験の計算手順はこちら。
👉 一元配置実験の計算方法を完全図解|分散分析表を1から作る全手順
二元配置実験の計算手順はこちら。
👉 【完全図解】二元配置実験の計算方法|交互作用の「なぜ」まで手を動かして理解する
📊 直交表実験の場合
L4やL8などの直交表を使った実験でも、自由度の考え方は同じです。
| 直交表 | 実験回数 | 総自由度 | 列の自由度 |
|---|---|---|---|
| L4 | 4回 | 4 - 1 = 3 | 各列1 |
| L8 | 8回 | 8 - 1 = 7 | 各列1 |
| L16 | 16回 | 16 - 1 = 15 | 各列1 |
直交表の各列は2水準なので、自由度は「2 - 1 = 1」です。
L8直交表は7列あるので、総自由度7を7つの列(各自由度1)に分配していると考えられます。
直交表の使い方を完全図解した記事はこちら。
👉 【完全図解】L4直交表・L8直交表の使い方|実験回数を「魔法のように」減らす割り付けの全手順
📝 まとめ:自由度は「自由に決められる数」
- 自由度とは「自由に決められるデータの個数」のこと
- 自由度 = 全体の数 − 制約の数で計算する
- 分散を計算するとき平均を使うので、1つの制約が生まれる → n-1
- n で割ると分散が過小推定されるため、n-1 で割って補正する
- t検定(1標本)の自由度はn - 1
- t検定(2標本)の自由度はn₁ + n₂ - 2
- 分散分析では、因子の自由度は水準数 - 1
- 交互作用の自由度は各因子の自由度の積
自由度は、統計学の「縁の下の力持ち」です。
普段は意識しないかもしれませんが、分散の計算、t検定、F検定、分散分析…あらゆる場面で自由度が登場します。
この記事で学んだ「制約の数だけ引く」という感覚を身につければ、どんな問題でも自由度を正しく計算できるようになります。
- 分散と標準偏差の計算を復習する
- t検定の問題で自由度を計算してみる
- 分散分析表を自分で作成してみる
- 直交表実験の自由度を計算してみる
自由に値を決められるデータの個数。英語ではDegrees of Freedom(略してdf)。制約が1つ増えるごとに1つ減る。
標本から母集団の分散を推定するとき、n-1で割って計算する分散。過小推定を防ぐための補正がされている。
データに課される条件のこと。例:「平均が決まっている」「合計が決まっている」など。制約が1つあると、自由度が1つ減る。
真の値よりも小さく推定してしまうこと。分散をnで割ると、母分散よりも小さく計算されてしまう。
- □ 自由度の定義を説明できる
- □ なぜn-1で割るかを説明できる
- □ t検定(1標本)の自由度を計算できる
- □ t検定(2標本)の自由度を計算できる
- □ 一元配置実験の自由度を計算できる
- □ 二元配置実験の自由度を計算できる
- □ 交互作用の自由度を計算できる
📖 関連記事
この記事を読んだ方には、以下の記事もおすすめです。
📊 自由度をマスターすれば、統計学の「なぜ」が分かるようになります。
「制約の数だけ引く」を忘れずに!




