😰 こんな経験、ありませんか?
- 実験したけど「有意差なし」…本当に差がないの?
- サンプル数は「10個くらいでいいかな」と適当に決めた…
- 上司に「なぜn=30にしたの?」と聞かれて答えられなかった…
- 検出力(Power)って聞いたことあるけど、意味がわからない…
- 実験をやり直す時間もコストもない…最初から正しく計画したい!
💡 この記事の結論
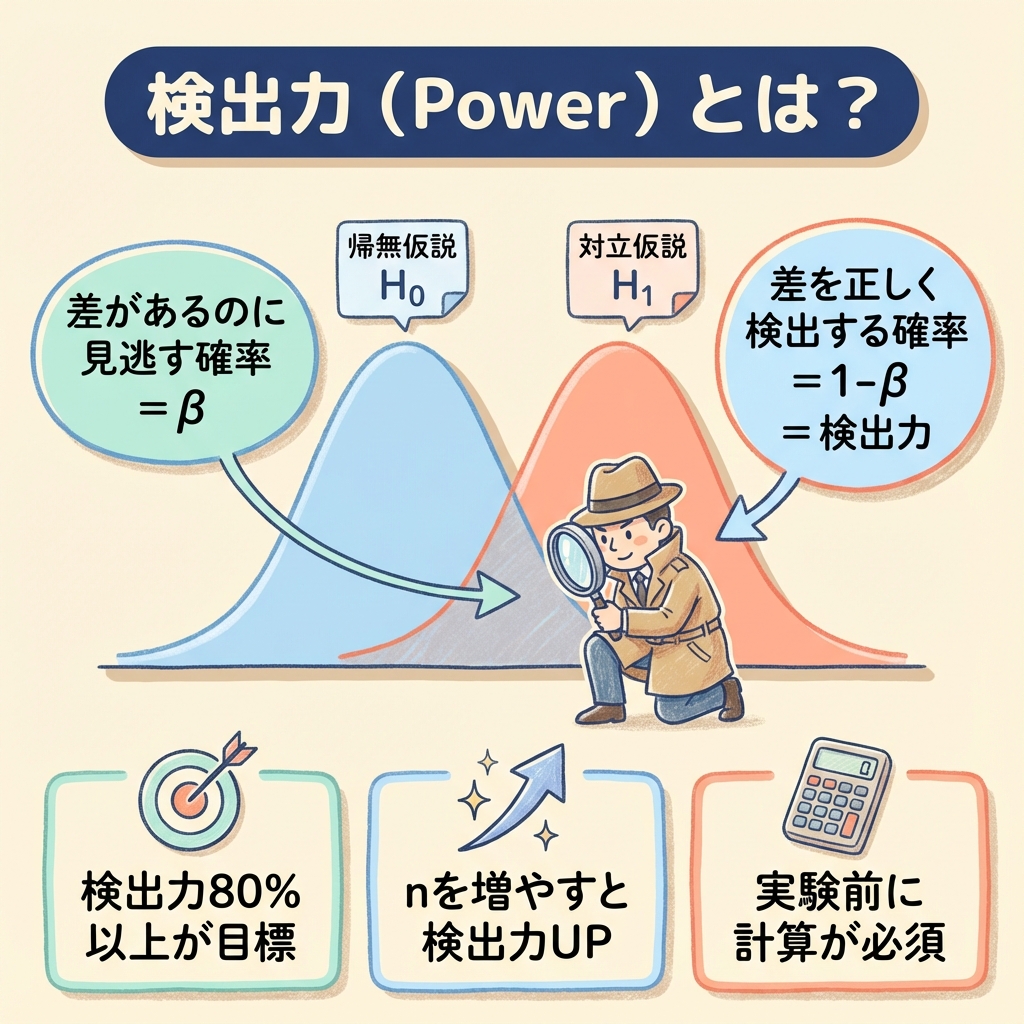
検出力(Power)とは、「本当に差があるとき、それを正しく検出できる確率」のことです。
検出力が低いまま実験すると、「差があるのに検出できない」という失敗を犯します。
これを防ぐには、実験前に必要なサンプルサイズnを計算しておく必要があります。
目安として検出力80%以上を確保できるnを設定しましょう。
📚 この記事でわかること
- 検出力(Power)の意味と重要性
- 第1種の過誤(α)と第2種の過誤(β)の関係
- 検出力を決める4つの要素
- 必要なサンプルサイズnの計算方法(具体例つき)
- 検出力分析の実務での活用法
📖 この記事を読む前に
「検定の基本」「有意水準α」「帰無仮説と対立仮説」がわかっていると、この記事がスムーズに読めます。
目次
なぜ「有意差なし」が問題になるのか?
まず、検出力を学ぶ必要性を理解するところから始めましょう。
😱 よくある失敗例
📋 ケース:新しい製造方法の効果検証
状況:新しい製造方法で品質が向上するか検証したい
実験:n=10のサンプルで検定を実施
結果:p = 0.08 で「有意差なし」
結論:「新方法は効果がない」と判断 → 採用見送り
⚠️ でも待ってください!
「有意差なし」=「効果がない」ではありません!
🔥 重要な真実
「有意差なし」という結果には、2つの可能性があります。
① 本当に差がない(新方法は効果なし)
② 差はあるけど、サンプル数が少なすぎて検出できなかった
もし②だった場合、本当は効果がある新方法を捨ててしまうという大損失になります。
この「差があるのに検出できない」という失敗を防ぐために必要なのが、検出力の考え方なのです。

2つの過誤を復習しよう
検出力を理解するには、まず「2種類の間違い」を整理する必要があります。
⚖️ 裁判で考える「2つの過ち」
統計検定を「裁判」に例えてみましょう。
被告人(=帰無仮説)を「有罪か無罪か」判断します。
| 本当は無実 (H₀が真) |
本当は犯人 (H₁が真) |
|
|---|---|---|
| 有罪判決 (H₀棄却) |
第1種の過誤(α) 冤罪!無実の人を有罪に |
正しい判断 犯人を有罪に ✓ |
| 無罪判決 (H₀採択) |
正しい判断 無実の人を無罪に ✓ |
第2種の過誤(β) 見逃し!犯人を無罪に |
📊 統計検定での「2つの過誤」
第1種の過誤(α)
「あわてんぼうの失敗」
本当は差がないのに
「差がある!」と判断してしまう
別名:生産者危険
通常 α = 0.05(5%)に設定
第2種の過誤(β)
「ぼんやり者の失敗」
本当は差があるのに
「差がない」と判断してしまう
別名:消費者危険
通常 β = 0.20(20%)以下を目標
💡 ポイント
有意水準 α は私たちが「5%」などと自分で決めます。
しかし β はサンプルサイズや効果の大きさに依存するため、意識的にコントロールしないと大きくなってしまいます。
そこで登場するのが「検出力」という考え方です。

検出力(Power)とは何か?
🔍 検出力の定義
検出力(Power)の定義
検出力 = 1 − β
「本当に差があるとき、それを正しく『差がある』と判断できる確率」
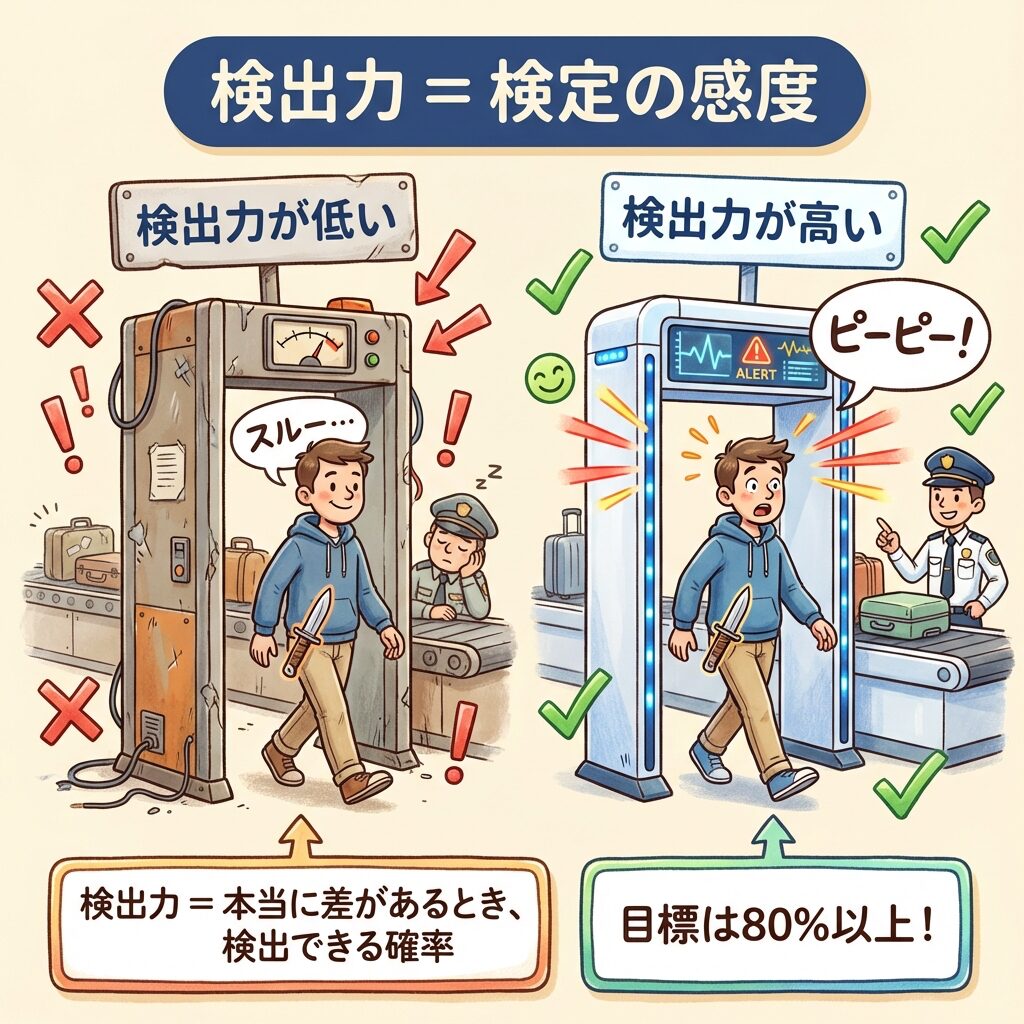
言い換えると、検出力とは「検定の感度」のようなものです。
🔬 例え話:金属探知機で考える
空港の金属探知機を想像してください。
🔔
検出力が高い探知機
金属があれば
ほぼ確実に反応する
🔕
検出力が低い探知機
金属があっても
反応しないことがある
検出力が低い探知機では、ナイフを持った人を見逃してしまうかもしれません。
これが統計検定における「第2種の過誤(β)」です。
検出力 = 1 − β なので、βを小さくすれば検出力が上がります。
📊 検出力の目安
| 検出力 | β(見逃し率) | 評価 |
|---|---|---|
| 50% | 50% | 危険:半分見逃す |
| 70% | 30% | やや不足 |
| 80% | 20% | 標準(最低ライン) |
| 90% | 10% | 良好 |
| 95% | 5% | 優秀(医薬品など) |
📌 業界標準
一般的な研究や品質管理では、検出力80%(β=0.20)以上が標準です。
医薬品の臨床試験など重要な場面では、90%以上を求められることもあります。
【図解】2つの分布で検出力を理解する
検出力を視覚的に理解するために、「2つの分布」を使って説明します。
これが理解できれば、検出力の本質がわかります。
🔔 2つの世界を想像しよう
統計検定では、2つの世界を同時に考えます。
🌍 世界A:帰無仮説(H₀)が正しい世界
「本当は差がない」世界
母平均 μ = μ₀(基準値)
🌍 世界B:対立仮説(H₁)が正しい世界
「本当は差がある」世界
母平均 μ = μ₁(μ₀からδだけズレている)
📊 2つの分布が重なるイメージ
2つの世界では、それぞれ標本平均の分布が存在します。
【イメージ図:2つの正規分布が重なっている】
重なっている部分が大きいほど、「差があるのに見逃す(β)」確率が高くなります。
つまり、検出力が低くなります。
🎯 α、β、検出力の位置関係
| 領域 | どの分布のどこ? | 意味 |
|---|---|---|
| α(有意水準) | H₀分布の端っこ(棄却域) | 差がないのに「ある」と誤判定する確率 |
| β | H₁分布の棄却域に入らない部分 | 差があるのに「ない」と誤判定する確率 |
| 検出力(1−β) | H₁分布の棄却域に入る部分 | 差があるときに正しく「ある」と判定する確率 |
💡 超重要ポイント
検出力を上げる=H₁分布が棄却域にたくさん入るようにする
そのためには…
① 2つの分布を離す(効果量を大きくする)
② 分布を細くする(サンプルサイズを増やす)
③ 棄却域を広くする(αを大きくする)※ただしトレードオフ
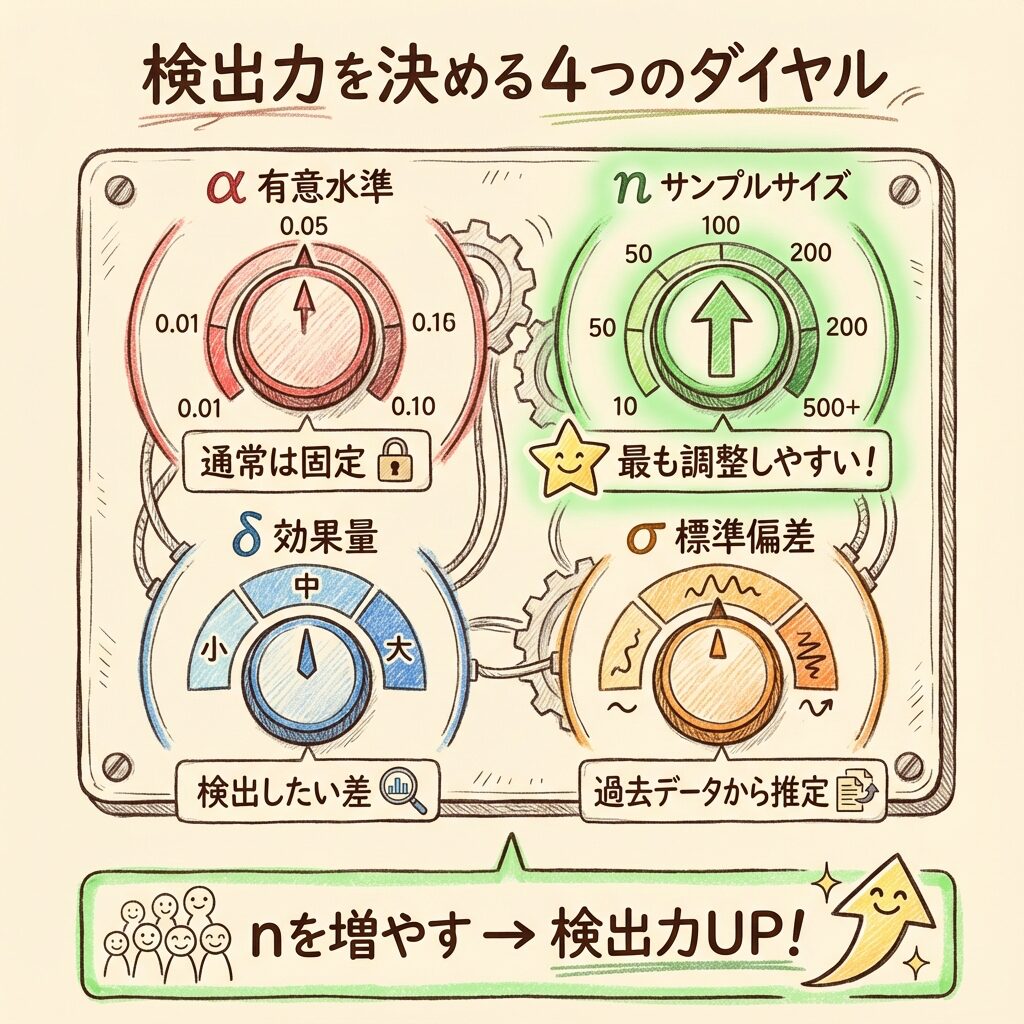
検出力を決める「4つの要素」
検出力は、4つの要素によって決まります。
これを理解すれば、「どうすれば検出力を上げられるか」がわかります。
🎛️ 4つのダイヤル
ダイヤル①
有意水準 α
αを大きくすると検出力UP
αを小さくすると検出力DOWN
※通常は α=0.05 で固定
(安易に変えるべきではない)
ダイヤル②
サンプルサイズ n
nを大きくすると検出力UP
nを小さくすると検出力DOWN
⭐ 最も調整しやすい!
実験前に計算して決める
ダイヤル③
効果量 δ(デルタ)
効果量が大きいと検出力UP
効果量が小さいと検出力DOWN
「検出したい差の大きさ」
事前に「この程度の差を見つけたい」と設定
🎯 標準化効果量 d(Cohen's d)
効果量δと標準偏差σは、まとめて1つの指標にできます。
これが「標準化効果量 d」です。
標準化効果量(Cohen's d)の公式
d = δ / σ = (μ₁ − μ₀) / σ
「検出したい差(δ)」を「バラつき(σ)」で割って標準化したもの。
単位に依存しないので、異なる研究間で比較できます。
📊 Cohen's d の目安
| d の値 | 効果の大きさ | イメージ |
|---|---|---|
| 0.2 | 小さい(Small) | 目を凝らさないとわからない差 |
| 0.5 | 中程度(Medium) | 注意すれば気づく差 |
| 0.8 | 大きい(Large) | 一目でわかる差 |
💡 実務でのヒント
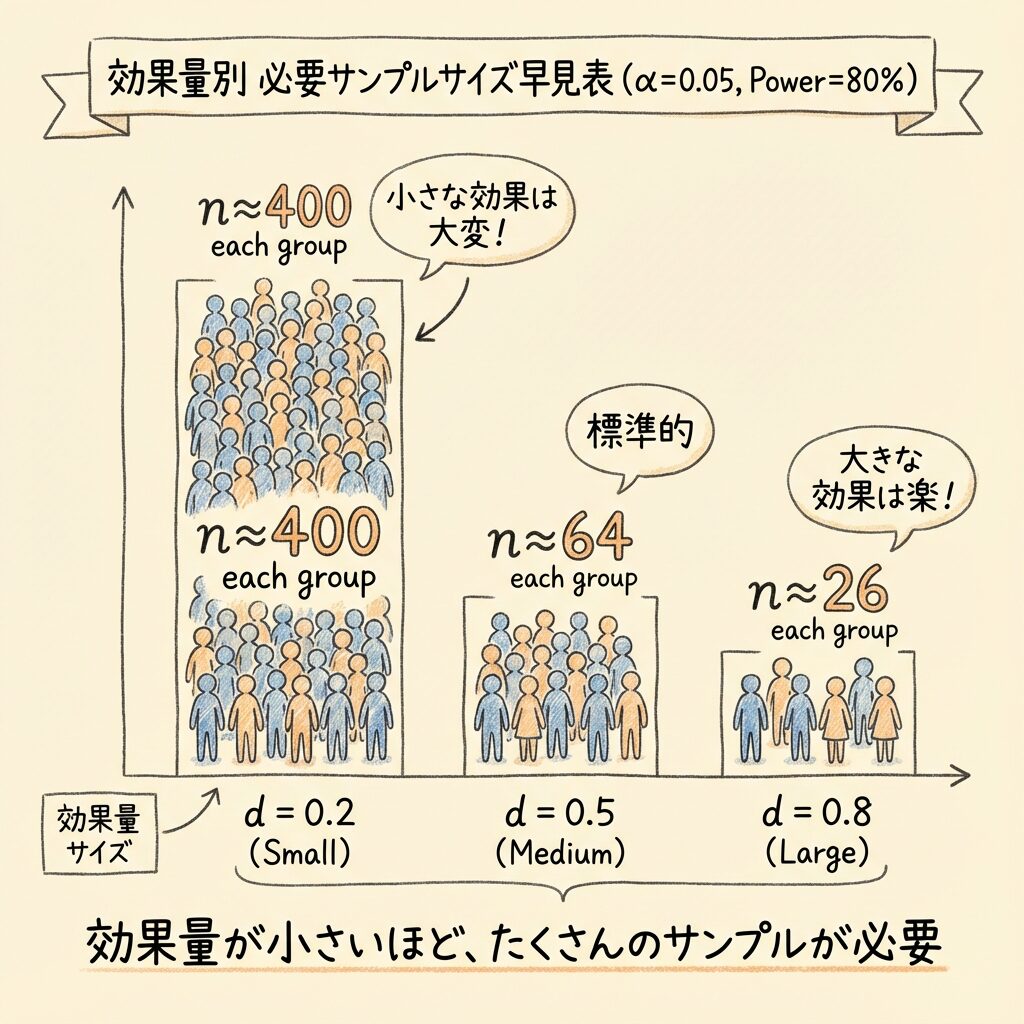
効果量 d が小さいほど、検出するのに大きなサンプルサイズが必要になります。
例えば d=0.2 の小さな効果を検出力80%で検出するには、各群 n≈400 も必要です!
一方、d=0.8 の大きな効果なら、各群 n≈26 で十分です。
分散と標準偏差|「バラつき」を数値化する魔法の公式 →
サンプルサイズ n の計算公式
いよいよ、必要なサンプルサイズを計算する公式を学びましょう。
検定の種類によって公式が異なりますが、基本的な考え方は同じです。
📐 1標本t検定の場合
サンプルサイズの公式(1標本)
n = (zα/2 + zβ)² × σ² / δ²
※厳密にはt分布を使いますが、n≧30程度なら正規分布(z)で近似できます
📐 2標本t検定の場合(各群のサンプルサイズ)
サンプルサイズの公式(2標本、各群)
n = 2 × (zα/2 + zβ)² × σ² / δ²
※2群を比較するので、1標本の2倍必要
📋 公式に出てくる記号
| 記号 | 意味 | よく使う値 |
|---|---|---|
| zα/2 | 有意水準αに対応するz値(両側) | α=0.05 → 1.96 |
| zβ | 検出力(1-β)に対応するz値 | β=0.20(Power=80%) → 0.84 β=0.10(Power=90%) → 1.28 |
| σ | 母標準偏差(過去データから推定) | 事前調査で決定 |
| δ | 検出したい差(効果量) | 「この程度の差を見つけたい」 |
🔢 よく使うz値の一覧
zα/2(両側検定)
α = 0.10 → z = 1.645
α = 0.05 → z = 1.960
α = 0.01 → z = 2.576
zβ(検出力)
Power = 70% → z = 0.524
Power = 80% → z = 0.842
Power = 90% → z = 1.282
Power = 95% → z = 1.645
💡 簡易公式(覚えやすい)
α=0.05、Power=80% のとき、zα/2 + zβ ≈ 1.96 + 0.84 = 2.80
この「2.8」を覚えておくと、概算が楽になります!
n ≈ 7.84 × σ² / δ² (1標本)
n ≈ 15.68 × σ² / δ² (2標本・各群)
【計算例】必要なサンプルサイズを求める
📋 例題:新しい製造方法の効果検証
🏭 状況設定
ある製品の引張強度(単位:MPa)を新方法で改善できるか検証したい。
既存方法:平均 μ₀ = 100 MPa、標準偏差 σ = 10 MPa(過去データより)
目標:5 MPa 以上の改善効果があれば「意味がある」と考える(δ = 5)
条件:有意水準 α = 0.05(両側)、検出力 80% 以上を確保
問い:何個のサンプルを測定すればよいか?
📝 STEP 1:必要な情報を整理
| 有意水準 α | 0.05(両側) |
| 検出力 (1-β) | 0.80(80%) |
| 母標準偏差 σ | 10 MPa |
| 検出したい差 δ | 5 MPa |
📝 STEP 2:z値を確認
zα/2:α = 0.05 の両側検定 → z = 1.96
zβ:Power = 80%(β = 0.20)→ z = 0.84
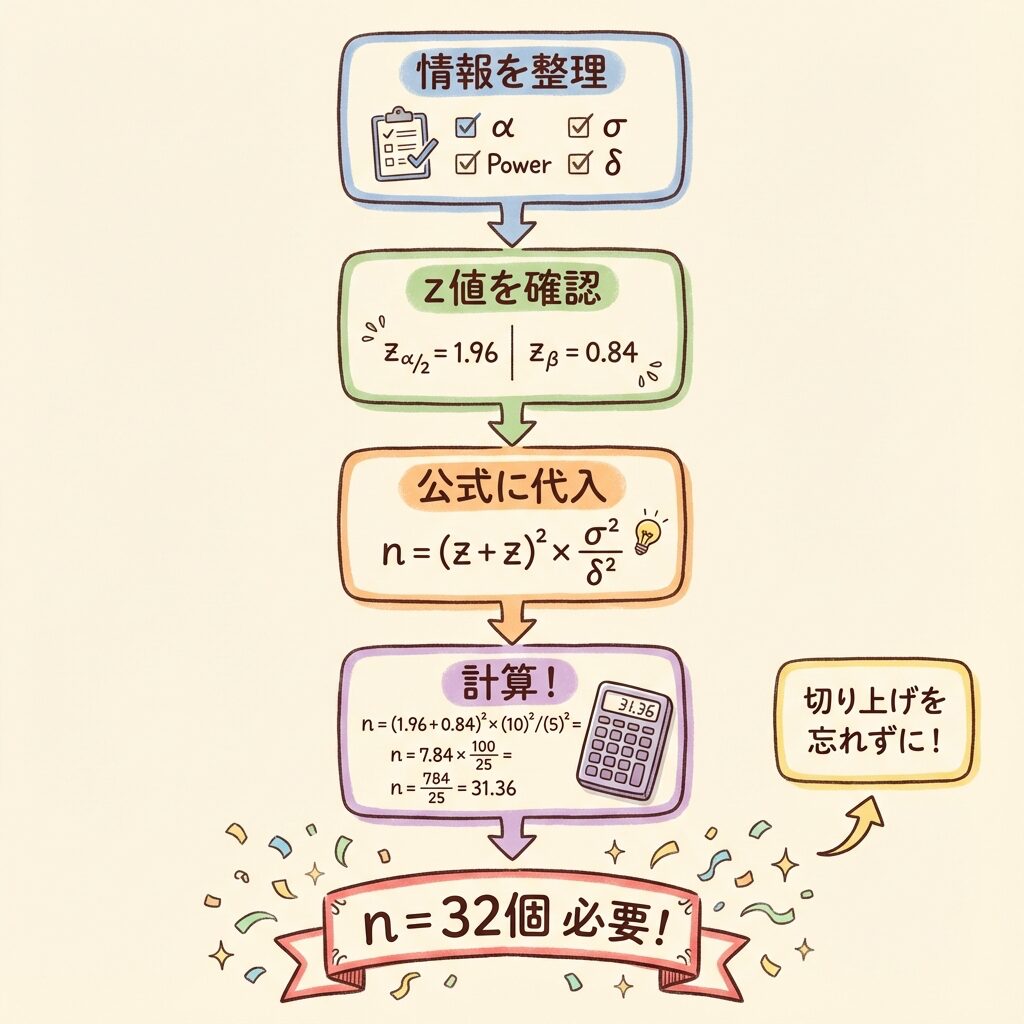
📝 STEP 3:公式に代入(1標本の場合)
n = (zα/2 + zβ)² × σ² / δ²
n = (1.96 + 0.84)² × 10² / 5²
n = (2.80)² × 100 / 25
n = 7.84 × 4
n = 31.36 → n = 32個(切り上げ)
📝 STEP 4:結論
📊 結論
5 MPa の改善効果を検出力80%で検出するには、
最低 32個 のサンプルが必要です。
もし n=10 で実験していたら、検出力は約35%しかなく、
65%の確率で「効果なし」と誤判定してしまうところでした。
📊 検出力と必要サンプルサイズの関係
同じ条件で、検出力を変えると必要なサンプルサイズがどう変わるか見てみましょう。
| 検出力 | β | zβ | 必要なn |
|---|---|---|---|
| 70% | 0.30 | 0.52 | 25個 |
| 80% | 0.20 | 0.84 | 32個 |
| 90% | 0.10 | 1.28 | 42個 |
| 95% | 0.05 | 1.64 | 52個 |
💡 ポイント
検出力を80%から90%に上げるだけで、必要なサンプル数は32個 → 42個に増えます。
検出力を上げたいなら、それだけコストと時間がかかることを覚えておきましょう。
実務では「検出力80%」が費用対効果のバランスが良いとされています。
【計算例2】2群を比較する場合
📋 例題:A工場とB工場の品質比較
🏭 状況設定
A工場とB工場の製品品質(平均値)に差があるか検証したい。
過去データ:標準偏差 σ = 8 (両工場とも同程度と仮定)
目標:3 以上の差があれば検出したい(δ = 3)
条件:α = 0.05(両側)、検出力 80%
問い:各工場から何個ずつサンプリングすればよいか?
📝 計算
n = 2 × (zα/2 + zβ)² × σ² / δ²
n = 2 × (1.96 + 0.84)² × 8² / 3²
n = 2 × 7.84 × 64 / 9
n = 2 × 55.6
n = 111.2 → 各群 n = 112個(合計 224個)
📊 【便利】効果量別の必要サンプルサイズ早見表
標準化効果量 d を使えば、σやδを個別に考えなくても必要なサンプルサイズの目安がわかります。
以下は α=0.05(両側)、検出力80% の場合の早見表です。
| 効果量 d | 効果の大きさ | 1標本 必要n |
2標本 各群n |
2標本 合計 |
|---|---|---|---|---|
| 0.2 | 小 | 196 | 393 | 786 |
| 0.3 | 小〜中 | 88 | 175 | 350 |
| 0.5 | 中 | 32 | 64 | 128 |
| 0.8 | 大 | 13 | 26 | 52 |
| 1.0 | 大 | 8 | 17 | 34 |
💡 早見表の使い方
1. 「どの程度の差を検出したいか」を決める
2. 過去データから σ を推定する
3. d = δ/σ を計算する
4. 表から必要なサンプルサイズを読み取る
例:「1σの半分(d=0.5)程度の差を見つけたい」なら、2標本で各群64個必要
ウェルチのt検定|バラつきが違う2群を比較する方法 →

まとめ:検出力とサンプルサイズのポイント
| 検出力とは | 本当に差があるとき、正しく「差がある」と判断できる確率(1−β) |
| 目標値 | 一般的に 80%以上(医薬品などは90%以上) |
| 検出力を決める要素 | α(有意水準)、n(サンプルサイズ)、δ(効果量)、σ(標準偏差) |
| 調整すべき変数 | サンプルサイズ n(最も調整しやすい) |
| 計算のタイミング | 実験の「前」に行う(後からでは遅い!) |
💡 覚え方のコツ
「検出力」=「金属探知機の感度」
感度が低い探知機(検出力が低い検定)では、
ナイフを持った人(本当の差)を見逃してしまう!
✅ 実験前チェックリスト
☐ 検出したい効果量(δ)を決めたか?
☐ 過去データからσを推定したか?
☐ 有意水準α(通常0.05)を設定したか?
☐ 目標とする検出力(通常80%)を決めたか?
☐ 必要なサンプルサイズnを計算したか?
🎊
おめでとうございます!
これで「計量値データの平均に関する検定・推定」シリーズは完了です!
Z検定 → t検定(1標本・2標本)→ ウェルチ → 対応あり → 区間推定 → 検出力
と学んできました。実務でデータ分析をする力が身についたはずです!
📖 NEXT STEP
次は「計数値データの検定・推定」へ進もう!
ここまでは「長さ」「重さ」などの計量値を扱ってきました。
次は「不良品の個数」「賛成/反対の人数」などの計数値の検定を学びましょう。
母比率の検定やカイ二乗検定など、実務で頻出のテーマが待っています!