- 有意水準5%のとき、カイ二乗分布表の「0.05」と「0.95」のどっちを見ればいいの?
- 片側検定?両側検定?上側?下側?もう頭がパンクしそう…
- 検定統計量χ²の式の意味がわからない。なぜ二乗して足すの?
- 適合度検定と独立性検定と母分散の検定、全部ごちゃごちゃ…
- 「何を検定するか」で棄却域の見方が決まる法則
- 0.05と0.95を迷わず選べる判断フローチャート
- 検定統計量χ²の式を「期待と現実のズレ」でイメージ理解
- 3種類のカイ二乗検定の使い分け
カイ二乗検定で「0.05を見るの?0.95を見るの?」と迷ってしまう気持ち、よくわかります。私も学生時代、ここで何度もつまずきました。
でも安心してください。たった1つのルールさえ覚えれば、もう迷うことはありません。この記事では、そのルールと検定統計量の意味を、図解でわかりやすく解説します。
目次
まず結論!棄却域を決める「たった1つのルール」
最初に結論をお伝えします。覚えるべきルールはこれだけです:
「χ²が大きいほど怪しい」検定 → 上側(右側)だけを見る
「え、それだけ?」と思いましたか?はい、カイ二乗検定の大半は「上側検定」なんです。だから基本的には「0.05」の列を見ればOK。
ただし、母分散の検定だけは例外で、両側検定になることがあります。この違いを理解するために、まずは「なぜ上側なのか」を図で見ていきましょう。
なぜ「χ²が大きいほど怪しい」のか?
カイ二乗検定の検定統計量χ²は、「期待値からのズレの大きさ」を表しています。
- χ² = 0:期待通りピッタリ(ズレなし)
- χ²が小さい:期待からちょっとズレてる(誤差の範囲)
- χ²が大きい:期待から大きくズレてる(何かおかしい!)
つまり、χ²が大きいほど「帰無仮説が間違っている可能性が高い」ということ。だから「χ²が大きすぎたら棄却」=「上側(右側)を見る」となるのです。
カイ二乗分布表の「0.05」と「0.95」の意味
カイ二乗分布表を見ると、「0.995」「0.99」「0.975」「0.95」「0.05」「0.025」「0.01」「0.005」のような列がありますよね。これ、実は「上側確率」を表しています。
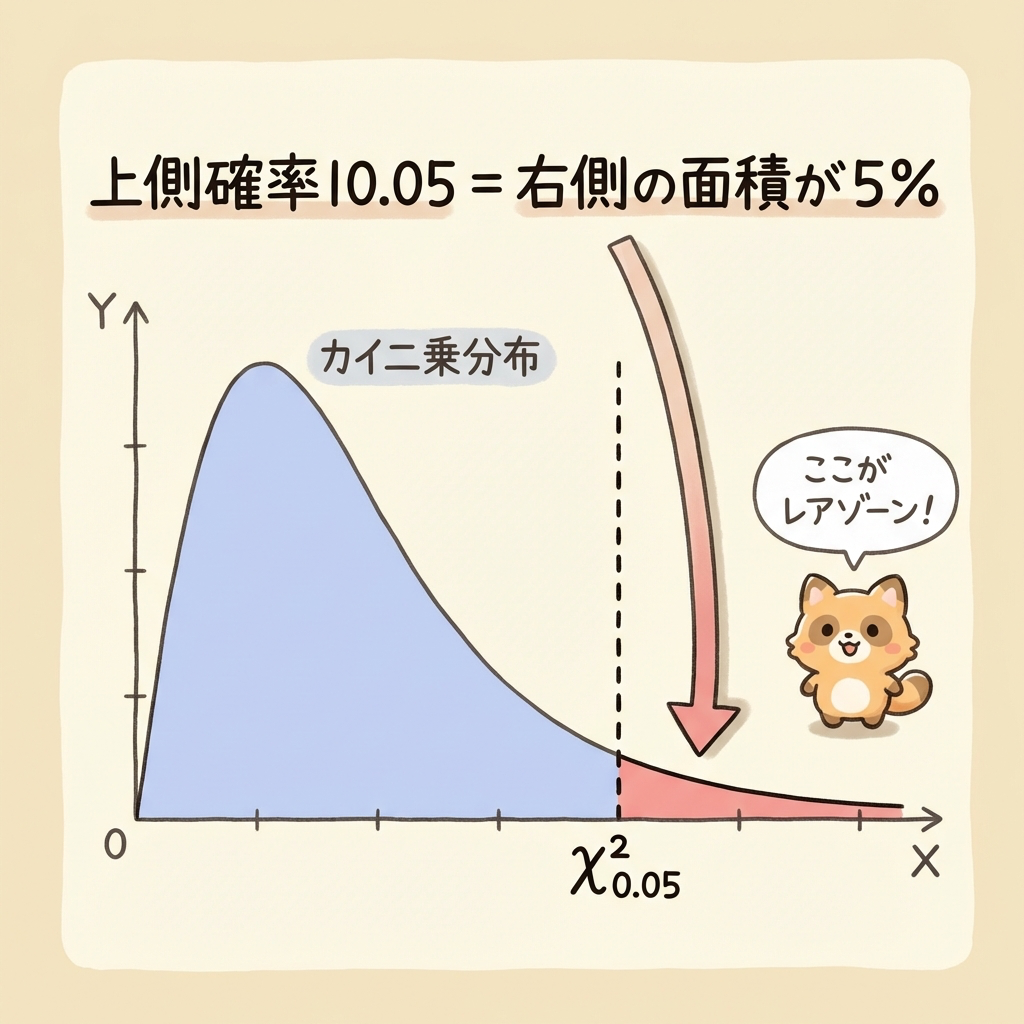
上側確率とは?「右側の面積」のこと
上側確率とは、「その値より右側(大きい側)の面積」のことです。
χ²₀.₀₅ の意味
右側の面積が5%になる点
→ これより右に行く確率は5%しかない
→ 「めったに起きない領域」の境界線
χ²₀.₉₅ の意味
右側の面積が95%になる点
→ これより右に行く確率は95%もある
→ 「ほとんどがここより右」の境界線
「0.05」は右側が5%だから、右端の"レアゾーン"の入口。
「0.95」は右側が95%だから、左端の"レアゾーン"の入口。
数字が小さいほど右側、数字が大きいほど左側と覚えましょう。
有意水準5%で見るべき値の早見表
| 検定の種類 | 片側/両側 | 見る列 | 棄却条件 |
|---|---|---|---|
| 適合度の検定 | 上側片側 | 0.05 | χ² > χ²₀.₀₅ |
| 独立性の検定 | 上側片側 | 0.05 | χ² > χ²₀.₀₅ |
| 母分散の検定(σ² ≠ σ₀²) | 両側 | 0.025 と 0.975 | χ² < χ²₀.₉₇₅ または χ² > χ²₀.₀₂₅ |
| 母分散の検定(σ² > σ₀²) | 上側片側 | 0.05 | χ² > χ²₀.₀₅ |
| 母分散の検定(σ² < σ₀²) | 下側片側 | 0.95 | χ² < χ²₀.₉₅ |
迷わないためのフローチャート
「結局どっちを見ればいいの?」という疑問を、フローチャートで一発解決しましょう。
棄却域を決めるフローチャート
独立性検定
χ²₀.₀₅ を使う
0.025と0.975
0.05
0.95
適合度・独立性検定は「0.05」一択!
母分散の検定だけ「対立仮説」を確認して判断する。
QC検定や統計検定では、適合度・独立性検定の出題が圧倒的に多いので、まず「0.05」と覚えておけばOKです。
検定統計量χ²の式の意味を理解する
次に、多くの人がつまずく「検定統計量χ²の式の意味」を解説します。式を丸暗記するのではなく、「何を計算しているのか」をイメージで理解しましょう。
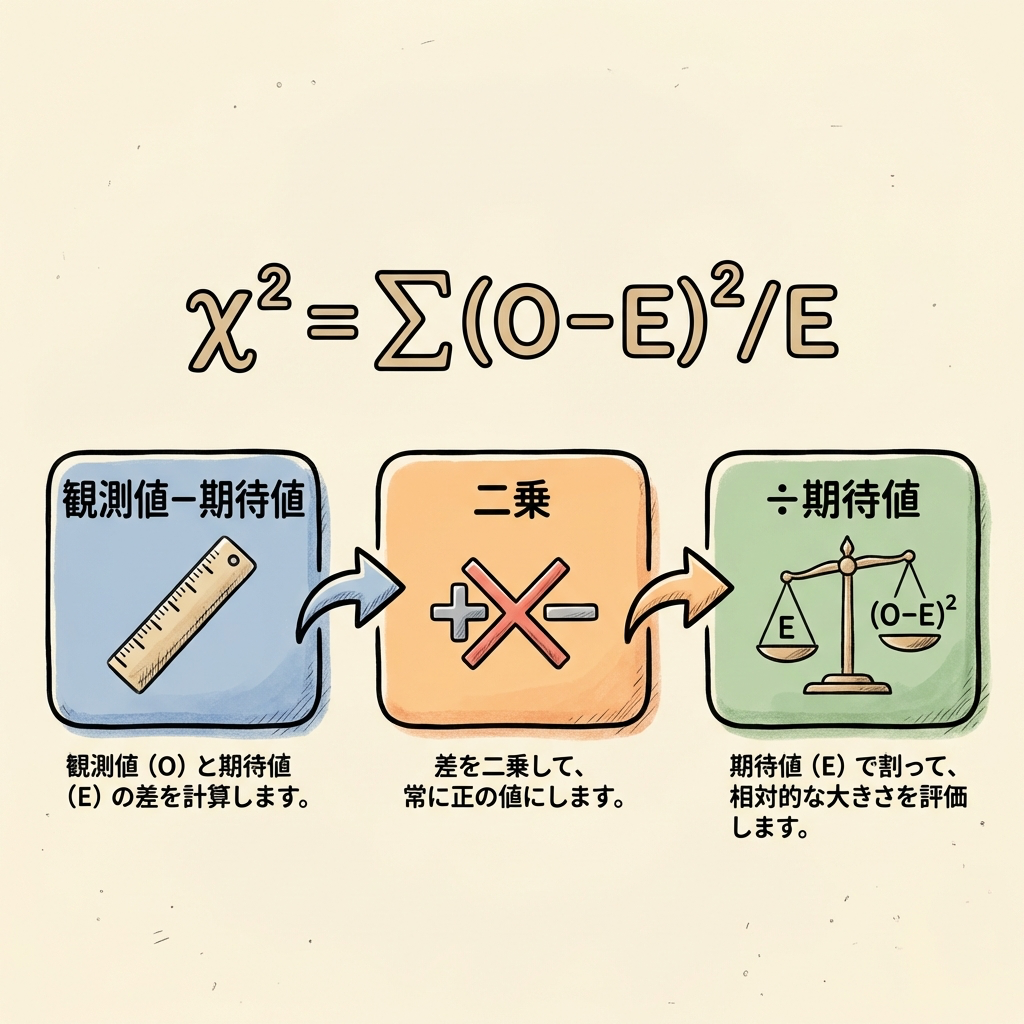
χ²の式:「期待と現実のズレ」を数値化する
この式を日本語で読むと、「期待と現実のズレを二乗して、期待値で割って、全部足す」です。なぜこんな計算をするのでしょうか?
式の各部分の意味を分解する
①「観測値 − 期待値」:ズレの大きさ
これは単純に「実際の値」と「理論上あるべき値」の差です。
期待値:各目が10回ずつ出るはず(60回 ÷ 6目)
観測値:1の目が15回出た
ズレ:15 − 10 = 5回分のズレ
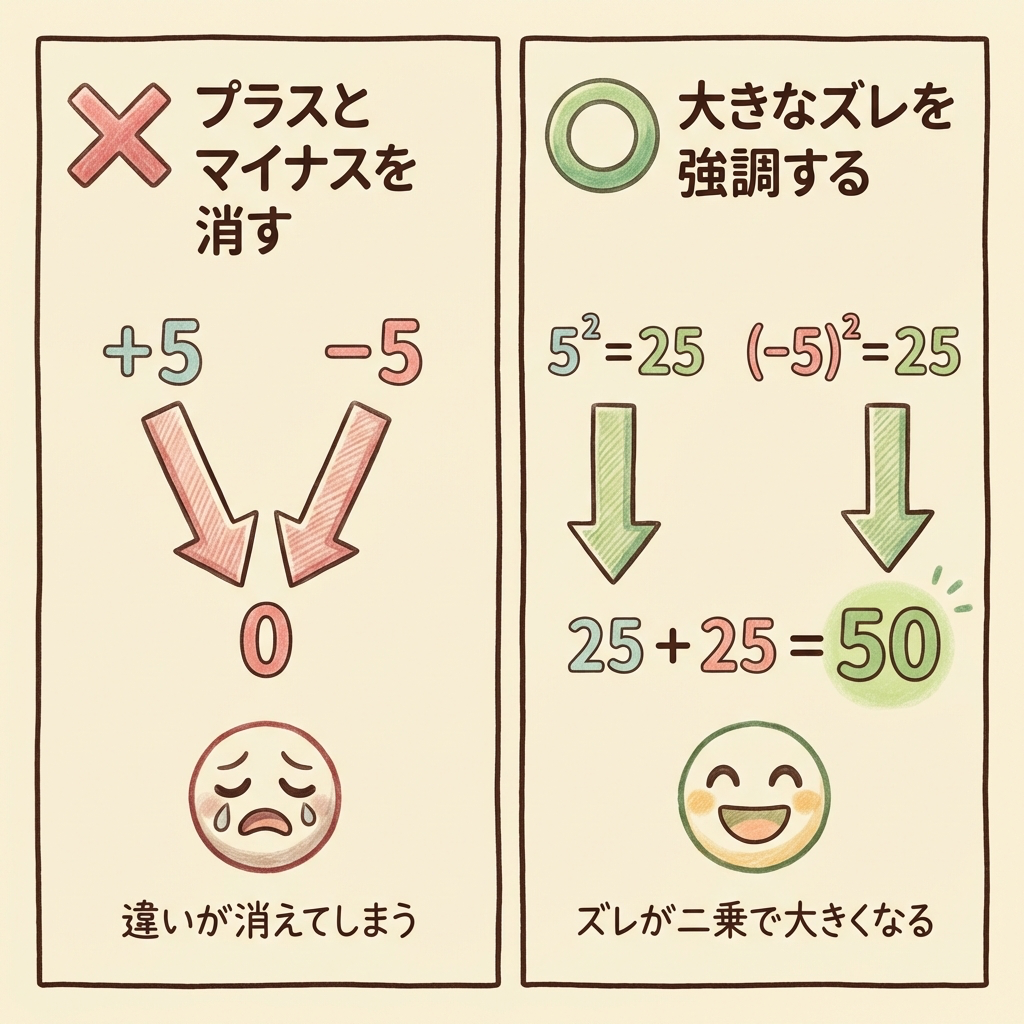
②「二乗する」:プラスとマイナスを消す&大きなズレを強調
なぜ二乗するのか?理由は2つあります:
- 理由1:ズレには「+5」と「−5」があるが、そのまま足すと相殺されてしまう。二乗すれば全部プラスになる。
- 理由2:大きなズレほど「怪しい」ので、二乗で強調する。ズレが2倍なら、影響は4倍になる。
③「期待値で割る」:スケールを揃える
これが意外と大事なポイントです。「同じ5のズレでも、期待値によって重みが違う」からです。
期待値10に対してズレ5
5²/10 = 2.5
期待の50%もズレてる!
結構怪しい…
期待値100に対してズレ5
5²/100 = 0.25
期待の5%しかズレてない
誤差の範囲かな
期待値で割るのは、「ズレの相対的な大きさ」を見るため。
テストで100点満点中5点のズレと、10点満点中5点のズレでは、後者の方が深刻ですよね。それと同じです。
具体例で計算してみよう
サイコロの例で、実際にχ²を計算してみましょう。
サイコロを60回振った結果が以下の通り。このサイコロは公正か?(有意水準5%)
| 出目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 観測値 O | 15 | 8 | 12 | 7 | 11 | 7 |
| 期待値 E | 10 | 10 | 10 | 10 | 10 | 10 |
| O − E | +5 | −2 | +2 | −3 | +1 | −3 |
| (O−E)²/E | 2.5 | 0.4 | 0.4 | 0.9 | 0.1 | 0.9 |
χ² = 2.5 + 0.4 + 0.4 + 0.9 + 0.1 + 0.9 = 5.2
棄却域との比較
自由度 = カテゴリ数 − 1 = 6 − 1 = 5
有意水準5%の上側臨界値:χ²₀.₀₅(5) = 11.07
χ² = 5.2 < 11.07 = χ²₀.₀₅(5)
→ 帰無仮説を棄却できない
「このサイコロは公正である」という仮説を否定する証拠は不十分。
つまり、このズレは誤差の範囲内と判断される。

母分散の検定だけ「両側」になる理由
ここまで「上側を見ればOK」と言ってきましたが、母分散の検定だけは例外です。なぜでしょうか?
検定の種類によって「何を疑うか」が違う
| 検定の種類 | 帰無仮説 H₀ | 対立仮説 H₁ | 棄却域 |
|---|---|---|---|
| 適合度検定 | 分布は理論通り | 分布は理論と違う | 上側のみ |
| 独立性検定 | 2変数は独立 | 2変数は独立でない | 上側のみ |
| 母分散検定 (両側) |
σ² = σ₀² | σ² ≠ σ₀² | 両側 |
適合度検定・独立性検定では、「ズレがあるかないか」だけを見ます。ズレの方向(どちらにズレているか)は問題にしません。だから「χ²が大きい=ズレが大きい」という上側だけを見ればOK。
一方、母分散の検定(σ² ≠ σ₀²)では、「バラつきが大きすぎる」だけでなく「小さすぎる」も疑う場合があります。だから上側と下側の両方を見る必要があるのです。
母分散検定の3パターン
「バラつきが変わったか?」(両側検定)
H₁: σ² ≠ σ₀² → 0.025と0.975を見る
「バラつきが大きくなったか?」(上側片側検定)
H₁: σ² > σ₀² → 0.05を見る
「バラつきが小さくなったか?」(下側片側検定)
H₁: σ² < σ₀² → 0.95を見る
品質管理の現場では、「バラつきが大きくなった(品質悪化)」を検出したいケースが多いので、上側片側検定(パターン②)がよく使われます。
逆に「新しい機械でバラつきが減ったか検証したい」場合は、下側片側検定(パターン③)を使います。
よくある間違いと対処法
最後に、カイ二乗検定でよくある間違いとその対処法をまとめます。
間違い①:「有意水準5%だから0.95を見る」
「5%だから…95%の方?」と混乱してしまう
カイ二乗分布表の数字は「上側確率」です。
「右側の面積が5%になる点」を知りたいなら、「0.05」の列を見ます。
「右側の面積が95%になる点」(=左側が5%)を知りたいなら、「0.95」の列を見ます。
間違い②:「適合度検定で両側検定をしてしまう」
「ズレがプラスにもマイナスにもなるから両側?」と考えてしまう
適合度検定のχ²は「ズレの二乗和」なので、必ず正の値になります。
χ²が大きい=ズレが大きい=帰無仮説が怪しい、なので上側だけを見ればOK。
「χ²が小さすぎて怪しい」というケースは存在しません(χ²=0は完璧に一致なので)。
間違い③:「母分散検定でいつも両側を見る」
「母分散検定=両側」と暗記してしまう
母分散検定でも、対立仮説によって片側か両側かが変わります。
H₁: σ² ≠ σ₀² → 両側
H₁: σ² > σ₀² → 上側片側
H₁: σ² < σ₀² → 下側片側
問題文の対立仮説を必ず確認しましょう。
まとめ|もう迷わない!カイ二乗検定の棄却域
- 適合度検定・独立性検定は「0.05」の列を見る(上側片側検定)
- 母分散検定は対立仮説を確認して、上側・下側・両側を判断する
- 検定統計量χ²は「期待と現実のズレ」を数値化したもの
- 二乗するのはプラス/マイナスを消す&大きなズレを強調するため
- 期待値で割るのはスケールを揃えるため(相対的なズレを見る)
カイ二乗検定の棄却域で迷う原因は、「何を検定しているか」を意識していないからです。「χ²が大きいほど怪しい」という原則を押さえておけば、もう迷うことはありません。
公式を丸暗記するのではなく、「何を疑っているのか」「どうなったら怪しいのか」というストーリーで理解すると、忘れにくくなります。統計学は、データの向こう側にある「真実」を探る探偵のような学問です。
📚 次に読むべき記事
適合度検定の計算手順を具体例で詳しく解説。カイ二乗検定の定番問題をマスターしよう。
クロス集計表から期待度数を計算し、2変数の関連性を検定する方法を解説。
「どの検定を使えばいい?」を一発解決。検定選びのフローチャートで迷わない。
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


