🎯 この記事でわかること
✅ なぜデータが少ない時に正規分布を使うと危険なのか?
✅ t分布が「裾が広い」理由を直感的に理解
✅ 正規分布とt分布の使い分けのポイント
✅ ビール会社から生まれた「Student」の物語
目次
はじめに|「また新しい分布?正規分布で十分でしょ?」
統計学を勉強していると、こう思いませんか?
「正規分布を覚えたのに、また別の分布?なんでこんなに種類があるの…?」
その気持ち、よくわかります。でも、t分布は「正規分布では対応できない問題」を解決するために生まれた、超実用的な分布なんです。
一言で言えば——
「データが少ない時でも、信頼できる分析がしたい!」
という切実な願いから生まれた分布。
今回は、「なぜ正規分布ではダメなのか?」という本質的な問いから始めて、t分布の正体に迫っていきましょう。
第1章|「データが少ない」という現実
まず、私たちが直面する「現実」を見てみましょう。
🏪 シナリオ:開店したばかりのカフェ
あなたは先週、念願のカフェをオープンしました。
1週間の売上データを見て、こう思いました。
「平均売上が1日4万円を超えていれば、このまま続けられる。でも、たった7日分のデータで判断していいの?」
これが「小標本問題」です。
📊 なぜ「データが少ない」と困るのか?
サイコロで考えてみましょう。
| 振る回数 | 平均値の安定性 | 例 |
|---|---|---|
| 3回 | 超不安定 | 1, 1, 2 → 平均1.3 / 6, 6, 5 → 平均5.7 |
| 30回 | やや安定 | 大体 3.0〜4.0 に収束 |
| 1000回 | 超安定 | ほぼ 3.5(理論値)に収束 |
データが少ないと、「たまたま」の影響がめちゃくちゃ大きくなるのです。
7日分の売上データも同じ。たまたま雨の日が多かったり、たまたまイベントと重なったりすると、「本当の実力」とはかけ離れた数字になりかねません。

第2章|正規分布の「傲慢さ」を暴く
ここからが本題です。なぜ正規分布を使うと危険なのか?
📐 正規分布の「前提条件」
正規分布を使うには、実は大きな前提があります。
母集団の標準偏差(σ)がわかっていること
でも、現実を考えてください。
🏪 カフェの売上の「真のバラつき」? → 知らない
💊 新薬の効果の「真のバラつき」? → 知らない
🏭 新製品の品質の「真のバラつき」? → 知らない
そう、私たちは「真のバラつき」なんてほとんど知らないのです。
だから、手元のデータから「推定」するしかない。この「推定値」を使うところに、問題が生じます。
🎯 たとえ話:射撃の「腕前」を測る
あなたは射撃場で、的の中心からどれくらいズレるか(バラつき)を測りたい。
ケースA:1000発撃った
計算された「バラつき」は、本当の腕前をかなり正確に反映している。これなら信用できる!
ケースB:5発しか撃ってない
計算された「バラつき」は、たまたまの結果に大きく左右される。たまたま調子が良かっただけかも…信用できない!
少ないデータから計算した「バラつき」は、それ自体がバラついているのです。
⚡ 正規分布の「傲慢さ」
正規分布は、この問題を無視します。
「手元のデータから計算したバラつきが、真のバラつきと同じだと思っていいよね?」
→ データが少ない時は、これが大問題!
5発しか撃ってないのに「俺の腕前はこれだ!」と断言するようなもの。自信過剰です。
第16回:【完全解説】正規分布とは?|統計の王様を初心者向けに徹底図解 →

第3章|t分布の「謙虚さ」
ここで登場するのがt分布です。
t分布は、正規分布と違って「謙虚」です。
「データが少ないから、計算したバラつきは不確かかもしれない。だから、その不確かさも考慮に入れて、裾を広げておこう」
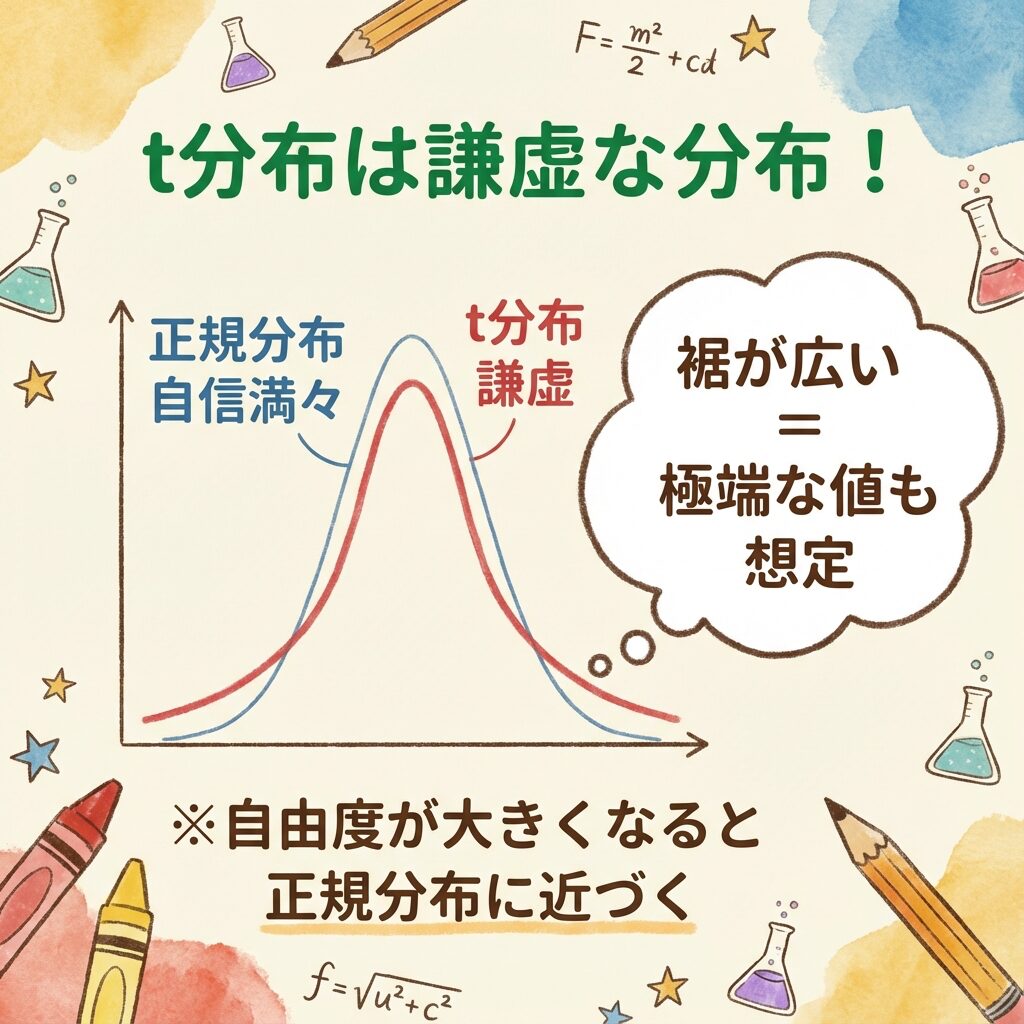
📊 「裾が広い」とはどういうことか?
正規分布とt分布を重ねてみましょう。
正規分布(細身)
∧
/ \
/ \
/ \
/ t分布(裾が広い)
/ ∧ \
/ / \ \
/_/______\_____\
←極端な値が出やすい→
t分布は「裾」が正規分布より広い。これは何を意味するか?
🎯 裾が広い = 極端な値が出やすいと想定している
データが少ない時は「たまたま」の影響が大きいから、普通じゃない値が出る可能性を高めに見積もっている。これが「謙虚さ」の正体。
🔑 自由度:t分布の「形」を決めるパラメータ
t分布には「自由度」という重要なパラメータがあります。
自由度によって、t分布の「形」が変わります。
| 自由度 | 分布の形 | イメージ |
|---|---|---|
| 小さい(1〜5) | 裾がかなり広い | 「データ少なすぎ…何が起こるかわからん」 |
| 中程度(6〜29) | やや広い | 「まあまあ信用できるけど、油断禁物」 |
| 大きい(30以上) | 正規分布とほぼ同じ | 「これだけあれば安心!」 |
自由度が大きくなると(データが増えると)、t分布は正規分布に近づいていく。
逆に言えば、データが少ない時こそ、t分布の「謙虚さ」が活きる!
【完全図解】自由度とは?|「なぜn-1で割るのか」を中学生でも分かるように解説 →
第4章|t分布誕生の物語 〜ビール会社の品質管理〜
ここで、t分布がどのように生まれたのか、その歴史を見てみましょう。
🍺 1908年、アイルランドのダブリン
ギネスビールで有名なギネス社で働く統計学者、ウィリアム・シーリー・ゴセットさんには、大きな悩みがありました。
ゴセットさんの悩み
「ビールの品質をチェックしたいけど、毎日何百本も検査するわけにはいかない…。せいぜい10〜20本が限界だ」
当時、品質管理といえば正規分布を使うのが常識でした。でも、正規分布は「データがたくさんある」ことが前提。少ないデータで使うと、信頼性に問題が…。
💡 画期的な発見
そこでゴセットさんは考えました。
「少ないデータでも使える、新しい分布を作れないかな?」
研究の結果、ついに「データ数が少ない時の不確かさを考慮した分布」を発見!これが現在のt分布です。
🎭 なぜ「Student」なのか?
でも、ギネス社は社員の研究成果を外部発表することを禁止していました。
そこでゴセットさんは、「Student(学生)」という偽名で論文を発表したのです!
だから今でも…
t分布 → 「Student's t-distribution」
t検定 → 「Student's t-test」と呼ばれる
普段飲んでいるビールの品質管理から生まれた分布が、今では世界中で使われているなんて、素敵な話ですよね!
第5章|正規分布 vs t分布 徹底比較
ここで、正規分布とt分布の違いを整理しておきましょう。
| 項目 | 正規分布 | t分布 |
|---|---|---|
| 使う場面 | データ30個以上 | データ30個未満 |
| 母分散 | 既知(わかっている) | 未知(わからない) |
| 分布の形 | 細身のベル型 | 裾が広いベル型 |
| 信頼区間 | 狭め | 広め(安全) |
| 態度 | 「自信満々」 | 「謙虚」 |
迷ったらt分布を使え!
t分布は正規分布より保守的(安全)なので、間違いが少ない。データが多ければ、どちらを使っても結果はほぼ同じになる。
t検定(母分散未知・一標本)「この部品の長さは規格通り?」実務で最も使う基本の検定 →

第6章|t分布が活躍する場面
t分布は、実は私たちの身近なところで大活躍しています。
🏭 場面①:製品の品質管理
「新製品の試作品が10個しかない。この品質は基準を満たしている?」
→ t分布で信頼区間を計算し、品質保証ができる。
💊 場面②:医薬品の効果測定
「治験参加者が20人だけ。この薬は効果がある?」
→ t検定で「効果あり」かどうかを統計的に判断できる。
📈 場面③:マーケティング効果測定
「A/Bテストの各グループが25人ずつ。どっちの広告が効果的?」
→ t検定で2つのグループを比較できる。
📚 場面④:教育効果の測定
「新しい教材を試したクラスが18人。成績は上がった?」
→ 対応のあるt検定で「ビフォー・アフター」を比較できる。
【保存版】統計検定の選び方フローチャート|計量・計数、対応あり・なしで迷わない最強の地図 →
まとめ|t分布は「小標本の味方」
🎯 t分布の正体
「データが少ない時でも、信頼できる分析がしたい!」という願いから生まれた、正規分布の「謙虚版」。
📊 なぜ「裾が広い」のか?
データが少ないと「たまたま」の影響が大きい。だから「極端な値が出やすい」と想定して、裾を広げている。これがt分布の「謙虚さ」。
🔑 使い分けのルール
データ30個未満 → t分布を使う
データ30個以上 → 正規分布でもOK
迷ったら → t分布を使う(安全)
t分布は「少ないデータでも諦めない」統計学の心意気を表しています。
完璧なデータが揃うまで待つのではなく、「今あるデータで最善を尽くす」。そんな現実的で力強い分布が、私たちの日常の意思決定を支えてくれています。
