- 「確率変数の和」の分散ってどう計算するの?
- 「独立」と「相関あり」で何が変わるの?
- 共分散と相関係数の関係がごちゃごちゃ…
- QC検定1級の部品組立問題が解けない
- 確率変数の和の「期待値」は常に足せる理由
- 独立な場合と相関がある場合の「分散」の違い
- 共分散と相関係数の関係をイメージで理解
- 部品組立問題をStep by Stepで完全攻略
製造現場では、複数の部品を組み合わせて1つの製品を作ります。
たとえば、「部品Aを2個と部品Bを1個を組み合わせて製品Cを作る」という場面。このとき、製品Cの長さの平均やバラつきはどうなるでしょうか?
これを理解するには、「確率変数の和」の知識が必要です。
この記事では、部品組立の具体例を使って、平均・分散・共分散の関係をイメージで徹底解説します。
目次
この記事で扱う問題の設定
まず、どんな問題を解くのかを把握しましょう。
【問題設定】部品の組立
部品Bの前後に部品Aを組み合わせて、製品Cを製造する。
製品C = 部品A(x₁)+ 部品B(y)+ 部品A(x₂)
| 部品 | 母平均 μ | 母標準偏差 σ |
|---|---|---|
| 部品A | 30.0 mm | 0.50 mm |
| 部品B | 15.0 mm | 0.20 mm |
規格:製品Cの長さは 73.5mm〜76.5mm の範囲内であること
🗺️ この問題で使う知識のロードマップ
| ステップ | 求めるもの | 使う知識 |
|---|---|---|
| Step 1 | 製品Cの平均 | 期待値の加法性 |
| Step 2 | 製品Cの分散(独立時) | 分散の加法性(独立版) |
| Step 3 | 不適合品率(独立時) | 正規分布と標準化 |
| Step 4 | 共分散の計算 | 共分散と相関係数の関係 |
| Step 5 | 製品Cの分散(相関あり) | 分散の加法性(相関あり版) |
| Step 6 | 不適合品率(相関あり) | 正規分布と標準化 |
それでは、順番に学んでいきましょう!
第8回:期待値 - 確率分布の中心を知る →
Step 1:確率変数の和の「期待値」は常に足せる
まず、最も基本的で重要な性質から学びましょう。
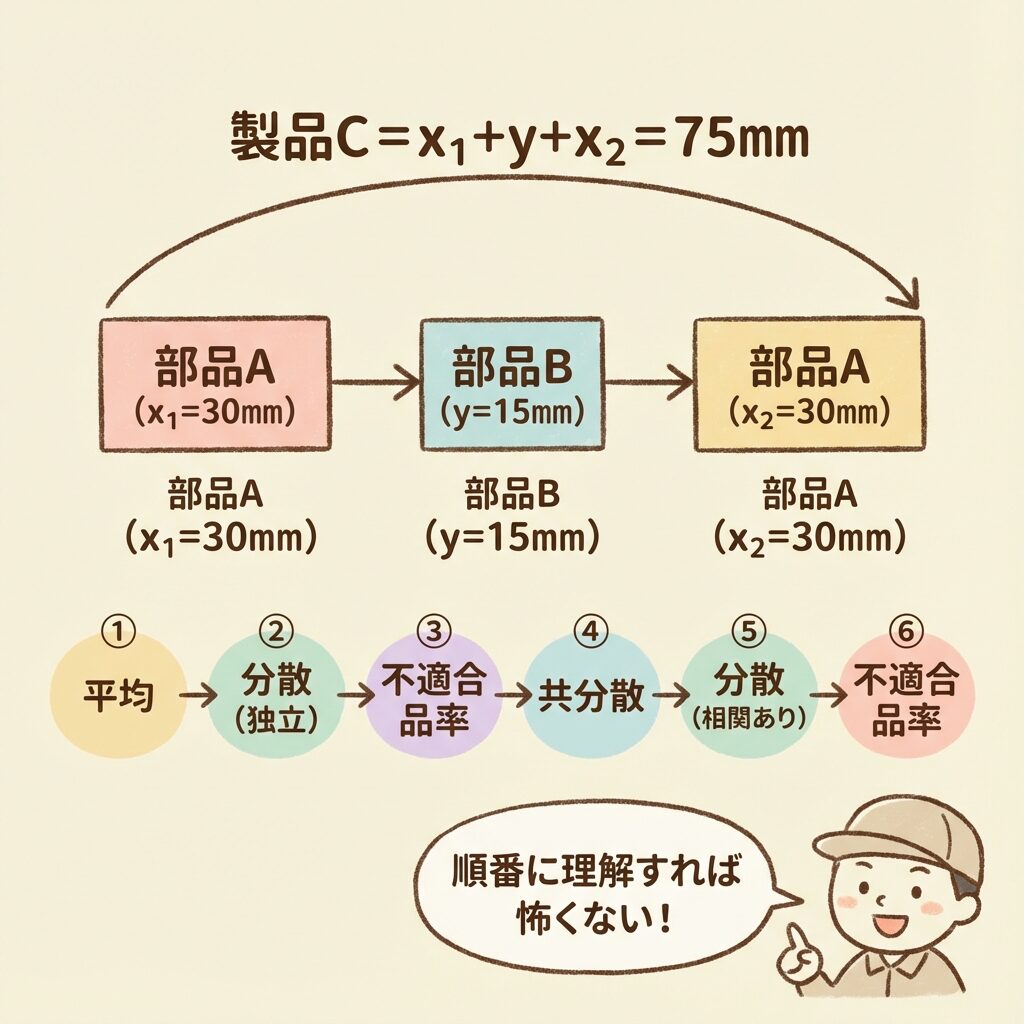
📐 期待値の加法性
E(X + Y) = E(X) + E(Y)
※ 独立でも相関があっても、常に成り立つ
これは統計学で最も重要な性質の一つです。どんな場合でも、確率変数の和の期待値は、それぞれの期待値の和になります。
🎯 イメージで理解:お小遣いの平均
こんな例で考えてみましょう。
【例】お父さんとお母さんからもらうお小遣い
- お父さんからもらう金額の平均:500円
- お母さんからもらう金額の平均:300円
合計のお小遣いの平均は? → 500 + 300 = 800円
「平均の合計 = 合計の平均」という直感的に当たり前のことが、数学的にも成り立つのです。
期待値の加法性は、XとYが独立でなくても(相関があっても)成り立ちます。
これは分散の場合と大きく異なります(分散は相関の影響を受ける)。
🧮 製品Cの平均を計算しよう
製品Cの長さ Z は、3つの確率変数の和です。
Z = x₁ + y + x₂
期待値の加法性を使うと:
E(Z) = E(x₁) + E(y) + E(x₂)
= 30.0 + 15.0 + 30.0
E(Z) = 75.0 mm
この計算は、作業者が「新人」でも「ベテラン」でも同じ結果になります。
なぜなら、期待値の加法性は相関の有無に関係なく成り立つからです。
第3回:平均値の奥深い世界 →
Step 2:独立な場合の「分散」の加法性
期待値は常に足せましたが、分散はそう単純ではありません。
まずは、確率変数が互いに独立な場合を考えましょう。
🤔 「独立」とは何か?
2つの確率変数が独立とは、「一方の値が他方に影響を与えない」ことを意味します。
【独立の例】
部品箱Ⅰから部品Aを1個、部品箱Ⅱから別の部品Aを1個、ランダムに選ぶ。
→ 1個目に大きい部品を選んでも、2個目の選び方には影響しない
→ この場合、x₁とx₂は独立
📐 分散の加法性(独立な場合)
V(X + Y) = V(X) + V(Y)
※ XとYが独立な場合のみ成り立つ
独立な確率変数の和の分散は、それぞれの分散の和になります。
🎯 イメージで理解:サイコロ2個の合計
サイコロを2個振る場合を考えてみましょう。
【例】サイコロ2個の合計
- サイコロ1個の分散:V(X) = 35/12 ≈ 2.92
- サイコロ2個は独立(1個目の出目は2個目に影響しない)
合計の分散:V(X₁ + X₂) = V(X₁) + V(X₂) = 2.92 + 2.92 = 5.84
独立なものを足すと、バラつきの「不確実性」が積み重なるので、分散は大きくなります。
2個のサイコロの合計の方が、1個のサイコロより「どんな値が出るか読めない」ですよね。
🧮 製品Cの分散を計算しよう(独立時)
標準的な作業者がランダムに部品を選ぶ場合、x₁, y, x₂ は互いに独立です。
分散の加法性より:
V(Z) = V(x₁) + V(y) + V(x₂)
ここで、分散 = (標準偏差)² なので:
- V(x₁) = (0.50)² = 0.25
- V(y) = (0.20)² = 0.04
- V(x₂) = (0.50)² = 0.25
V(Z) = 0.25 + 0.04 + 0.25 = 0.54
標準偏差 σ(Z) = √0.54 ≈ 0.735 mm
σ(Z) ≈ 0.735 mm
標準偏差をそのまま足してはいけません!
❌ 間違い:σ(Z) = 0.50 + 0.20 + 0.50 = 1.20 mm
✅ 正しい:分散を足してから、平方根を取る

Step 3:不適合品率を計算する(独立時)
製品Cの平均と標準偏差がわかりました。次に、規格から外れる確率(不適合品率)を計算しましょう。
📋 規格の確認
| 項目 | 値 |
|---|---|
| 規格下限 SL | 73.5 mm |
| 規格上限 SU | 76.5 mm |
| 母平均 μ | 75.0 mm |
| 母標準偏差 σ(独立時) | 0.735 mm |
📐 不適合品率の計算方法
不適合品率は、規格下限より小さい確率と規格上限より大きい確率の合計です。
不適合品率 = P(Z < SL) + P(Z > SU)
規格下限側のZ値
規格上限側のZ値
確率を標準正規分布表から読む
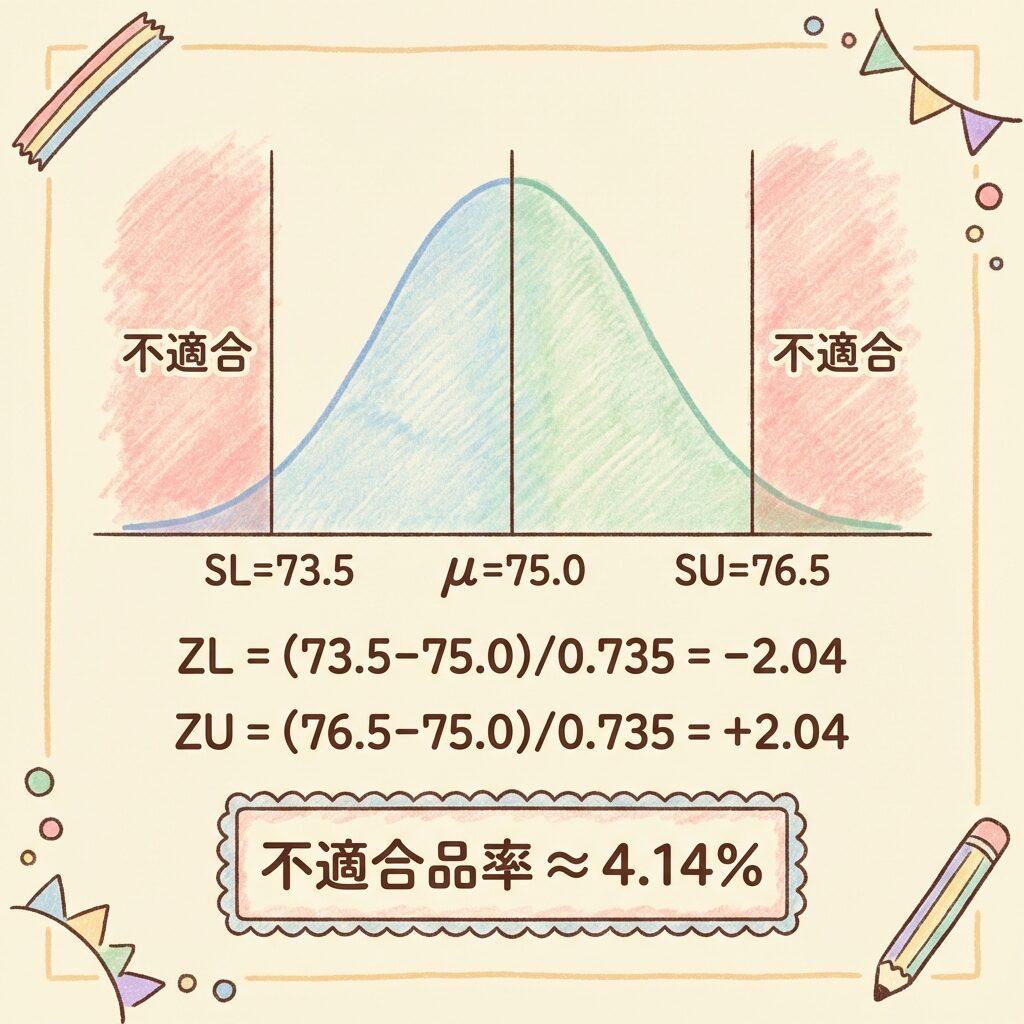
平均が規格の中央にあるので、上下対称です。
- P(Z < −2.04) ≈ 0.0207
- P(Z > +2.04) ≈ 0.0207
不適合品率 = 0.0207 + 0.0207 = 0.0414
約 4.14%
100個作ると約4個が規格外
🔗 Step 3:共分散と相関係数を理解する
💡 このステップのゴール
「共分散」と「相関係数」の意味を直感的に理解し、なぜ相関がある場合に分散の計算が変わるのかをイメージできるようになる。
🤝 共分散とは?「一緒に動く度合い」
共分散(Covariance)は、「2つの変数が一緒に動く傾向の強さと方向」を表す数値です。
イメージしやすいように、身近な例で考えてみましょう。
☕ 身近な例:気温とアイスクリームの売上
| 関係のタイプ | 例 | 共分散の符号 |
|---|---|---|
| 正の相関 | 気温↑ → アイス売上↑ | Cov > 0(正) |
| 負の相関 | 気温↑ → おでん売上↓ | Cov < 0(負) |
| 無相関 | 気温 と 株価(関係なし) | Cov ≈ 0 |
📐 共分散の公式
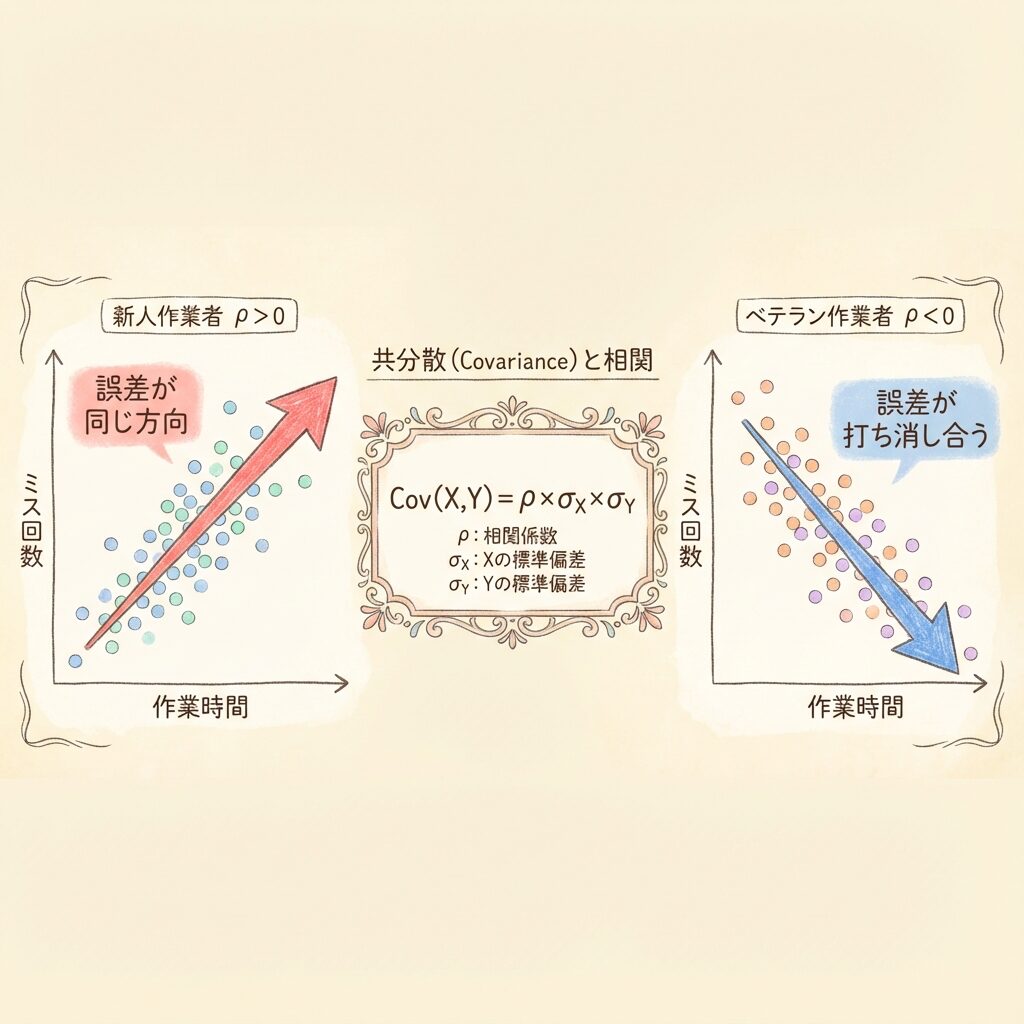
共分散は、相関係数 ρ(ロー)と各変数の標準偏差から計算できます。
📌 共分散の公式
ρ(ロー):相関係数(-1 ≤ ρ ≤ 1)
σX:変数Xの標準偏差
σY:変数Yの標準偏差
🎯 相関係数の意味
相関係数 ρ は、共分散を「標準化」したもので、-1 から +1 の範囲に収まります。
| 相関係数 ρ | 解釈 | イメージ |
|---|---|---|
| ρ = +1 | 完全な正の相関 | Xが増えると必ずYも増える |
| ρ = +0.5 | 中程度の正の相関 | Xが増えるとYも増える傾向 |
| ρ = 0 | 無相関(独立) | XとYは関係なし |
| ρ = -0.5 | 中程度の負の相関 | Xが増えるとYは減る傾向 |
| ρ = -1 | 完全な負の相関 | Xが増えると必ずYが減る |
🏭 部品組立における相関の意味
製造現場では、作業者の熟練度によって部品間に相関が生まれることがあります。
😰 新人作業者の場合
相関係数 ρ > 0(正の相関)
部品Aを大きく作りすぎたとき、部品Bも大きく作りすぎる傾向がある。
→ 誤差が同じ方向に重なるので、バラつきが増大!
😊 ベテラン作業者の場合
相関係数 ρ < 0(負の相関)
部品Aを大きく作ったとき、意識的に部品Bを小さく調整する。
→ 誤差が打ち消し合うので、バラつきが減少!
⚡ 重要ポイント
相関係数の符号が「正」か「負」かで、分散の計算結果が大きく変わります。これが次のステップで学ぶ「相関がある場合の分散の公式」につながります。
📊 Step 4:相関がある場合の分散の公式
💡 このステップのゴール
相関がある場合の分散の公式を理解し、「なぜ共分散の2倍を足すのか」を直感的にわかるようになる。
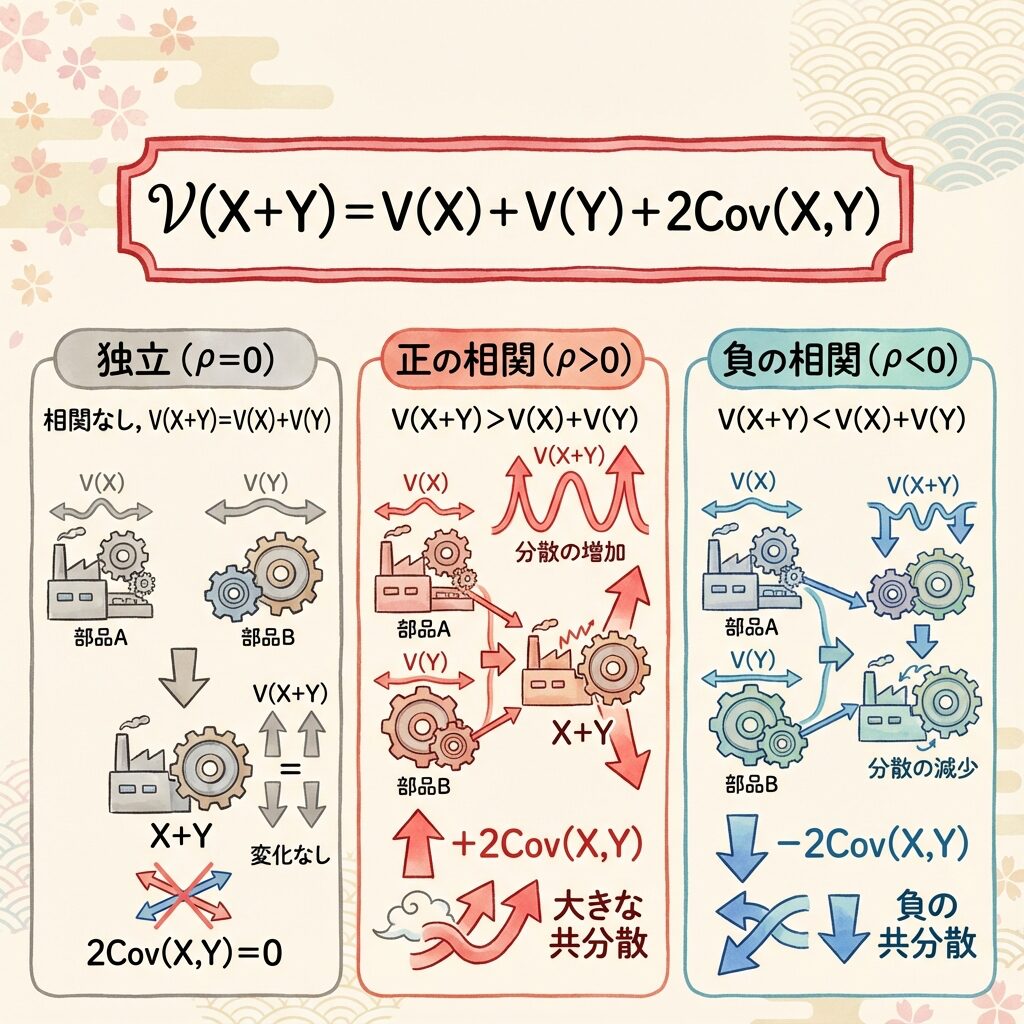
📐 相関がある場合の分散の公式
2つの確率変数 X と Y に相関がある場合、和 (X + Y) の分散は以下のようになります。
📌 相関がある場合の分散の公式
🤔 なぜ「2倍」を足すのか?
この公式、「なぜ共分散の2倍なの?」と疑問に思いませんか?
実は、数学的に展開すると自然に2が出てきます。詳しく見てみましょう。
📖 分散の定義から導出
分散の定義は「偏差の2乗の期待値」です。(X + Y) の分散を展開すると...
V(X + Y) = E[(X + Y - μX - μY)²]
= E[((X - μX) + (Y - μY))²]
= E[(X - μX)² + 2(X - μX)(Y - μY) + (Y - μY)²]
= E[(X - μX)²] + 2E[(X - μX)(Y - μY)] + E[(Y - μY)²]
= V(X) + 2 × Cov(X, Y) + V(Y)
中学校で習った(a + b)² = a² + 2ab + b²という展開公式と同じ構造ですね!
真ん中の「2ab」の部分が「2 × Cov(X, Y)」になっているのです。
🎯 相関の符号で分散はどう変わる?
| 相関の状態 | Cov(X, Y) | 分散への影響 | 品質への影響 |
|---|---|---|---|
| 独立(ρ = 0) | 0 | V(X) + V(Y) | 基準 |
| 正の相関(ρ > 0) | 正(+) | 増加する | バラつき増大 → 不良↑ |
| 負の相関(ρ < 0) | 負(-) | 減少する | バラつき減少 → 不良↓ |
🧮 3つ以上の変数の場合
今回の問題では、製品C = x₁ + y + x₂ と3つの変数の和になっています。
この場合、共分散のペアは以下の3通りです。
📝 3変数の場合の分散の公式
V(x₁ + y + x₂) = V(x₁) + V(y) + V(x₂)
+ 2 × Cov(x₁, y)
+ 2 × Cov(y, x₂)
+ 2 × Cov(x₁, x₂)
💡 今回の問題の設定
今回の問題では、部品Aと部品Bの間にのみ相関があり、部品A同士(x₁とx₂)は独立と仮定しています。
したがって Cov(x₁, x₂) = 0 となり、計算がシンプルになります。
✏️ 総合演習:部品組立問題を完全攻略!
🎯 このセクションのゴール
これまで学んだ知識をフル活用して、実際の問題をStep by Stepで解いていきます。自分でも手を動かしながら読み進めてください!
📋 問題の設定
🏭 製品Cの組立条件
製品Cは、部品A(2個)と部品B(1個)を組み合わせて製造します。
| 部品 | 母平均 μ | 母標準偏差 σ |
|---|---|---|
| 部品A(x₁, x₂) | 30.0 mm | 0.50 mm |
| 部品B(y) | 15.0 mm | 0.20 mm |
規格:73.5 mm ≤ 製品C ≤ 76.5 mm
📝 Step 1:製品Cの母平均を求める
期待値の加法性を使う
期待値(母平均)の加法性より、製品Cの母平均は各部品の母平均の和です。
✅ ポイント:この計算は相関の有無に関係なく成り立ちます!
📝 Step 2:独立な場合の分散と不適合品率
まず、すべての部品が独立(相関なし)と仮定した場合を計算します。
【分散の計算】
独立な場合、分散は単純に足し算できます。
V(C) = V(x₁) + V(y) + V(x₂)
= σ²A + σ²B + σ²A
= (0.50)² + (0.20)² + (0.50)²
= 0.25 + 0.04 + 0.25
= 0.54
標準偏差:σ(C) = √0.54 ≈ 0.735 mm
【不適合品率の計算】
製品Cは正規分布 N(75.0, 0.735²) に従います。規格は 73.5 mm ≤ C ≤ 76.5 mm です。
下側規格限界(SL = 73.5)のZ値:
上側規格限界(SU = 76.5)のZ値:
標準正規分布表より、P(Z < -2.04) ≈ 0.0207
両側の不適合品率 = 0.0207 × 2 ≈ 4.14%
📝 Step 3:新人作業者の場合(正の相関 ρ = +0.25)
😰 新人作業者の設定
部品Aと部品Bの間に正の相関 ρ = +0.25 がある。
(部品A同士 x₁ と x₂ は独立)
【共分散の計算】
Cov(A, B) = ρ × σA × σB
= 0.25 × 0.50 × 0.20
= 0.025
【分散の計算】
V(C) = V(x₁) + V(y) + V(x₂) + 2×Cov(x₁, y) + 2×Cov(y, x₂)
※ Cov(x₁, x₂) = 0(独立)なので省略
= 0.25 + 0.04 + 0.25 + 2×0.025 + 2×0.025
= 0.54 + 0.05 + 0.05
= 0.64
標準偏差:σ(C) = √0.64 = 0.80 mm
【不適合品率の計算】
Z値の計算:
P(Z < -1.875) ≈ 0.0304
両側の不適合品率 = 0.0304 × 2 ≈ 6.08%
⚠️ 独立時(4.14%)より約1.5倍に増加!
📝 Step 4:ベテラン作業者の場合(負の相関 ρ = -0.30)
😊 ベテラン作業者の設定
部品Aと部品Bの間に負の相関 ρ = -0.30 がある。
(部品A同士 x₁ と x₂ は独立)
【共分散の計算】
Cov(A, B) = ρ × σA × σB
= (-0.30) × 0.50 × 0.20
= -0.030
【分散の計算】
V(C) = V(x₁) + V(y) + V(x₂) + 2×Cov(x₁, y) + 2×Cov(y, x₂)
= 0.25 + 0.04 + 0.25 + 2×(-0.030) + 2×(-0.030)
= 0.54 - 0.06 - 0.06
= 0.42
標準偏差:σ(C) = √0.42 ≈ 0.648 mm
【不適合品率の計算】
Z値の計算:
P(Z < -2.31) ≈ 0.0104
両側の不適合品率 = 0.0104 × 2 ≈ 2.08%
✅ 独立時(4.14%)より約半分に減少!
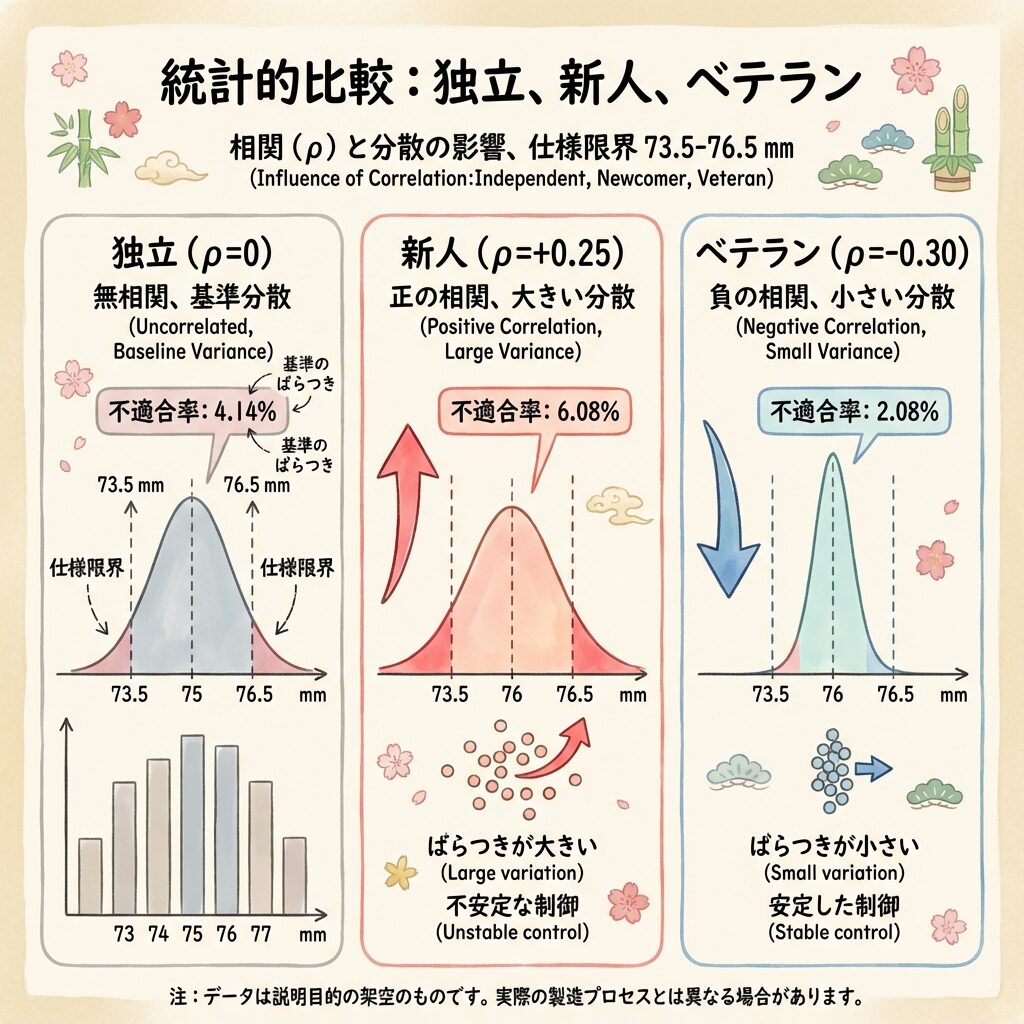
📊 結果の比較まとめ
| 条件 | 相関係数 ρ | 分散 V(C) | 標準偏差 σ | 不適合品率 |
|---|---|---|---|---|
| 独立 | 0 | 0.54 | 0.735 mm | 4.14% |
| 新人(正の相関) | +0.25 | 0.64 | 0.80 mm | 6.08% ↑ |
| ベテラン(負の相関) | -0.30 | 0.42 | 0.648 mm | 2.08% ↓ |
💡 この結果が意味すること
ベテラン作業者は、部品Aを大きめに作ったとき、意識的に部品Bを小さめに調整することで、製品全体のバラつきを抑えています。これが「負の相関」の力です。
品質管理の現場では、この「調整能力」を数値で評価し、作業者の熟練度を測る指標として活用できます。
📚 まとめ:この記事のポイント
✅ 押さえておくべき4つのポイント
1. 期待値(平均)の加法性
E(X + Y) = E(X) + E(Y) ← 相関の有無に関係なく成立!
2. 独立な場合の分散の加法性
V(X + Y) = V(X) + V(Y) ← 独立のときだけ成立
3. 相関がある場合の分散
V(X + Y) = V(X) + V(Y) + 2Cov(X, Y) ← 共分散の2倍を加える
4. 共分散の公式
Cov(X, Y) = ρ × σX × σY ← 相関係数と標準偏差から計算
📋 公式一覧(保存版)
| 公式名 | 公式 | 条件 |
|---|---|---|
| 期待値の加法性 | E(X + Y) = E(X) + E(Y) | 常に成立 |
| 分散の加法性(独立) | V(X + Y) = V(X) + V(Y) | 独立のみ |
| 分散の加法性(相関あり) | V(X + Y) = V(X) + V(Y) + 2Cov(X,Y) | 常に成立 |
| 共分散 | Cov(X, Y) = ρσXσY | 常に成立 |
| Z値(標準化) | Z = (X - μ) / σ | 常に成立 |
🔑 QC検定1級での出題ポイント
- 「共分散の符号」を問う問題 → 正の相関か負の相関かを判断
- 「分散の計算」→ 相関がある場合は +2Cov を忘れずに
- 「不適合品率の比較」→ 相関の符号で不良率が増減する
- 「3つ以上の変数の分散」→ 共分散のペアをすべて考慮
📖 次に読むべき記事
🎯 QC検定1級 合格を目指すあなたへ
この記事の内容をしっかり理解すれば、計数値・計量値問題の「確率変数の和」に関する問題は確実に解けるようになります。繰り返し読んで、公式と考え方を身につけてください!