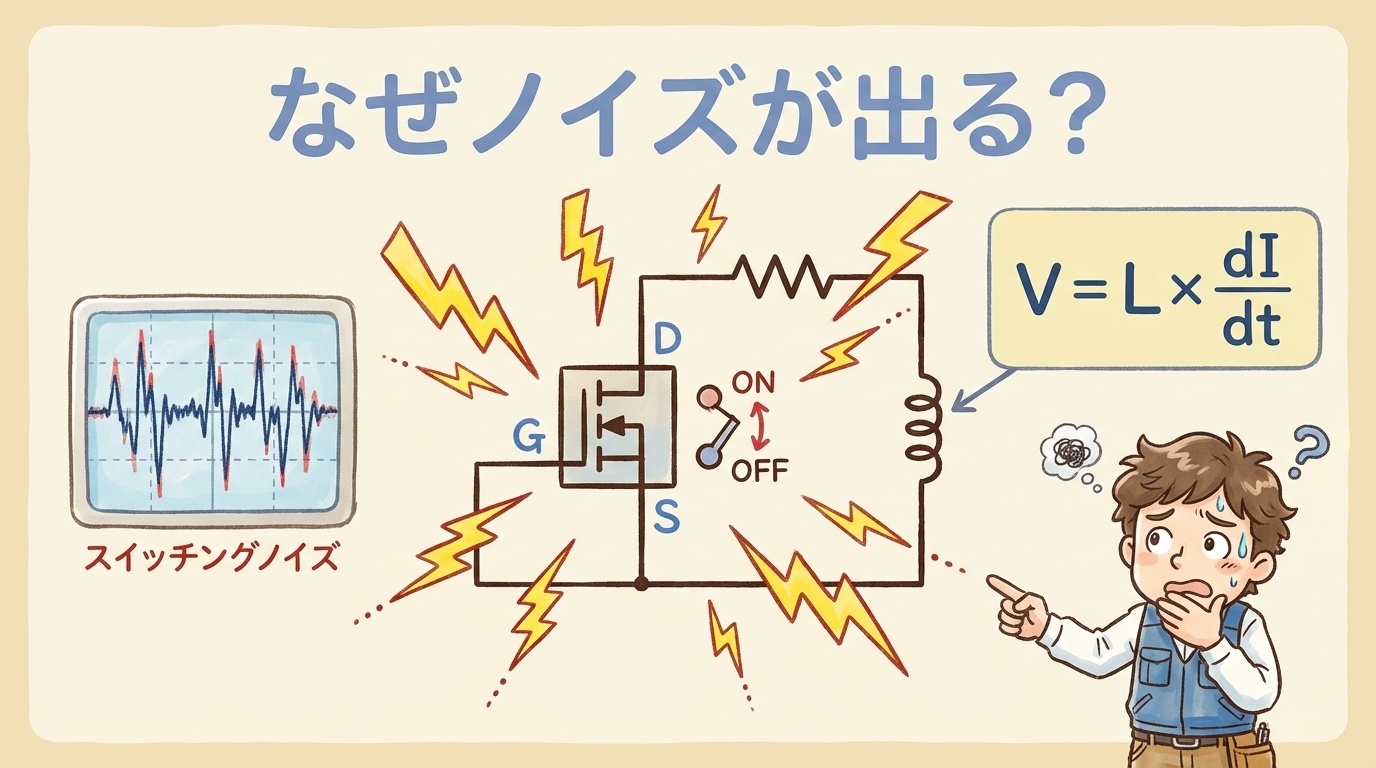
- スイッチングノイズって結局何が原因なの?
- 「V = L × dI/dt」の式は知ってるけど、イメージがわかない
- 寄生インダクタンスって何?目に見えないのに何で問題になるの?
- 「ループ面積を小さく」と言われるけど、なぜ効果があるの?
- スイッチングノイズの発生原因を「水道管のウォーターハンマー」で直感理解
- dI/dt(電流の急変)がノイズを生む仕組み
- 寄生インダクタンスを「配線に隠れたバネ」でイメージ
- ループ面積を小さくするとノイズが減る理由
「スイッチングノイズ対策しろって言われたけど、そもそもなんでノイズが出るの?」
パワエレ設計で必ずぶつかるこの疑問。
式は知っていても、「なぜそうなるのか」がわからない人が多いのではないでしょうか?
この記事では、スイッチングノイズの発生メカニズムを「水道管のウォーターハンマー」という身近な現象に例えて、徹底的にわかりやすく解説します。
この記事を読み終える頃には、「あ、だからループ面積を小さくするのか!」と腑に落ちるはずです。
目次
スイッチングノイズとは?|まず「現象」を理解する
スイッチングノイズの正体
パワエレ回路では、MOSFETやIGBTなどのスイッチング素子が高速でON/OFFを繰り返しています。
このON/OFFの瞬間に、本来あるべきでない高電圧のスパイク(突起)が発生します。
これがスイッチングノイズです。
│ │ │ │
┘ └───┘ └──
││ │ ││ │
┘└───┘∨ ┘└───┘∨
なぜスイッチングノイズは問題なのか?
スイッチングノイズは、以下のような深刻な問題を引き起こします。
| 問題 | 具体例 |
|---|---|
| 素子の破壊 | 電圧スパイクがMOSFETの耐圧を超え、素子が壊れる |
| 誤動作 | ノイズがマイコンや制御ICに侵入し、予期せぬ動作を引き起こす |
| EMI(電磁妨害) | ノイズが電波となって放射され、他の機器に悪影響を与える |
| 効率低下 | ノイズ成分が熱として失われ、電力変換効率が下がる |
「試作品は動いたのに、量産したら不良品が多発…」
原因を調べたら、スイッチングノイズによる誤動作だった、というケースは珍しくありません。
ノイズ対策は「後から」では手遅れになることが多いのです。
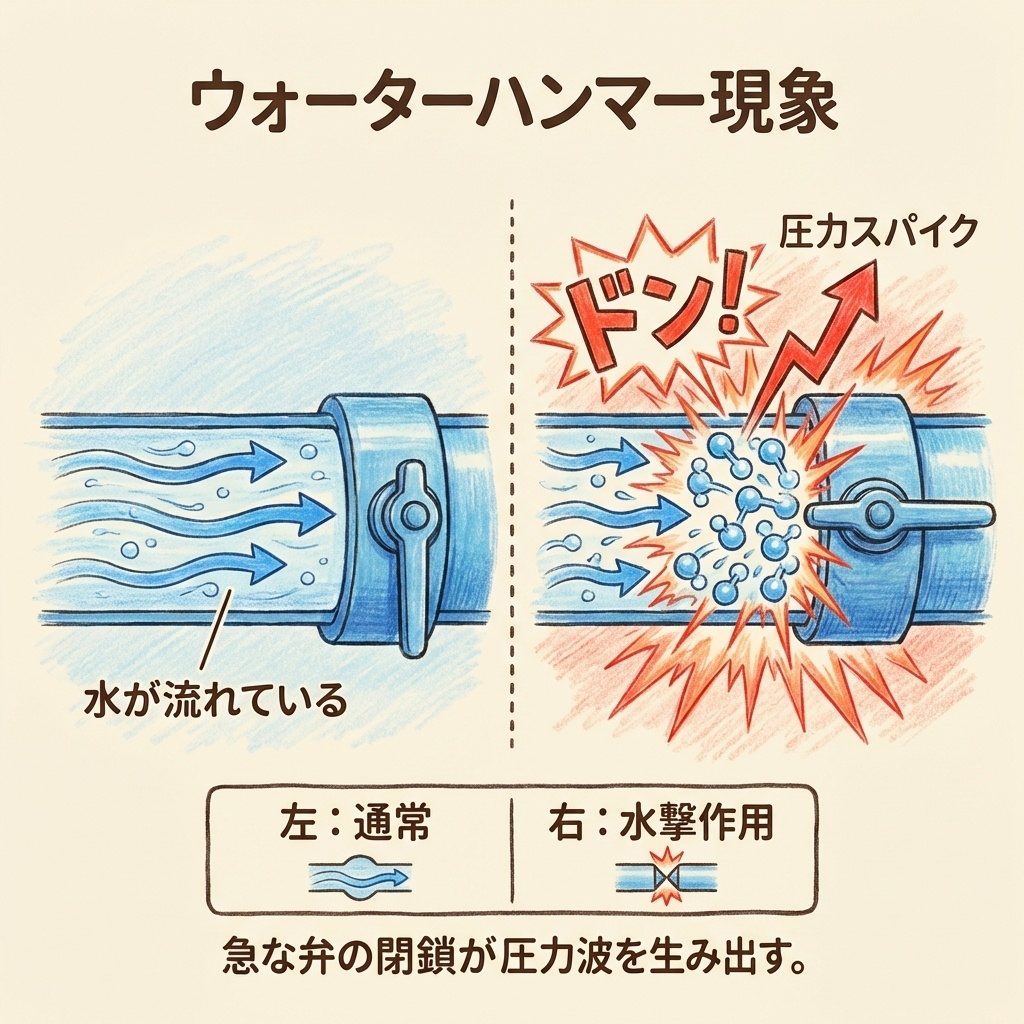
たとえ話:「ウォーターハンマー現象」で理解する
スイッチングノイズを理解するために、水道管の「ウォーターハンマー現象」をイメージしてみましょう。
ウォーターハンマーとは?
お風呂の蛇口を急に閉めると、「ドン!」「ガン!」という音がしたことはありませんか?
これがウォーターハンマー(水撃作用)です。
↓
衝撃なし ✅
↓
「ドン!」圧力スパイク発生 ❌
なぜ「ドン!」と音がするのか?
水道管の中を、水が勢いよく流れています。
この水には「慣性」があります。つまり、動いているものは動き続けようとする性質です。
蛇口を急に閉めると、水は急に止まれません。
行き場を失った水の運動エネルギーが、「圧力」に変換されます。
この圧力が配管を叩き、「ドン!」という音になるのです。
ひどい場合は、配管が破裂することもあります。
急に止める → 運動エネルギーが圧力スパイクに変換される
これがウォーターハンマーの正体です。
電気回路でも同じことが起きている!
実は、電気回路でもまったく同じ現象が起きています。
| 水道管 | 電気回路 |
|---|---|
| 水 | 電流(電子の流れ) |
| 水圧 | 電圧 |
| 蛇口 | スイッチング素子(MOSFET等) |
| 配管の太さ・長さ | インダクタンス(L) |
| 圧力スパイク(ドン!) | 電圧スパイク(ノイズ) |
蛇口を急に閉める = スイッチを急にOFFにする
電流も水と同じように「慣性」を持っています。
急に止めようとすると、行き場を失ったエネルギーが「電圧スパイク」となって現れるのです。
V = L × dI/dt|ノイズ発生の「物理法則」
ウォーターハンマーのイメージがつかめたところで、電気の言葉で説明しましょう。
スイッチングノイズの発生は、以下の式で表されます。
L:インダクタンス [H]
dI/dt:電流の時間変化率 [A/s]
この式が意味することは、とてもシンプルです。
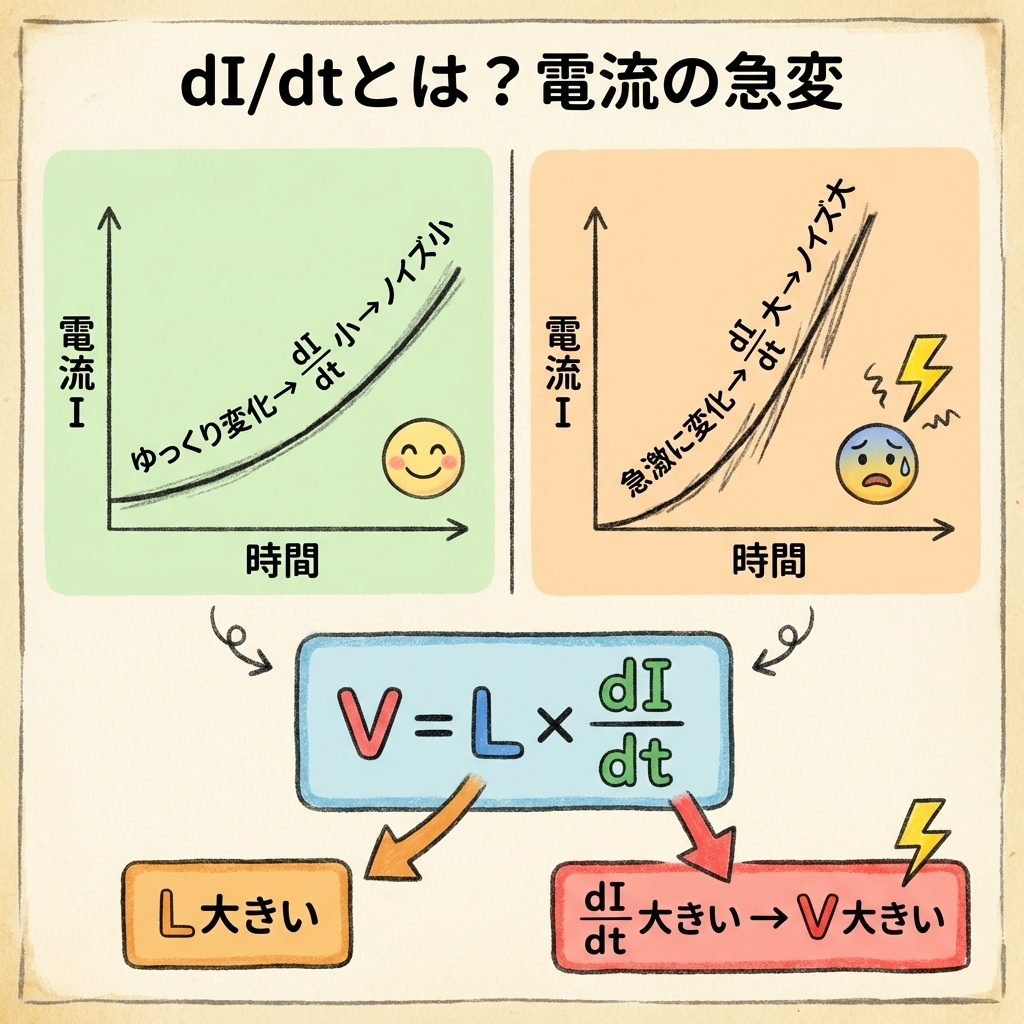
dI/dt とは?|「電流の急変度」
dI/dt(ディーアイ・ディーティー)は、「電流がどれだけ急激に変化したか」を表します。
「d」は「微小な変化」、「dt」は「微小な時間」という意味です。
つまり、「ごく短い時間に、電流がどれだけ変わったか」ということ。
(ゆっくり変化)
→ ノイズ小 ✅
(急激に変化)
→ ノイズ大 ❌
水道管の例えで言えば:
dI/dt 大 = 蛇口を急に閉める → 「ドン!」(圧力スパイク)
L(インダクタンス)とは?|「電流の慣性」
インダクタンス(L)は、「電流の変化を妨げる性質」を表します。
水道管の例えで言えば、「配管の太さや長さ」に相当します。
太くて長い配管ほど、中を流れる水の量(=慣性)が大きくなりますよね。
電気回路でも同じです。
Lが大きいほど、電流は「動き続けよう」とする力が強くなります。
インダクタンスLは「コイル」だけでなく、「配線そのもの」にも存在します。
これが次に説明する「寄生インダクタンス」です。
V = L × dI/dt の意味を日本語で言うと
この式を日本語で表現すると、こうなります。
電流の「慣性」の大きさ(L) × 電流の「急変度」(dI/dt)
つまり、ノイズを減らすには:
…のどちらか(または両方)を実現すればいいのです。
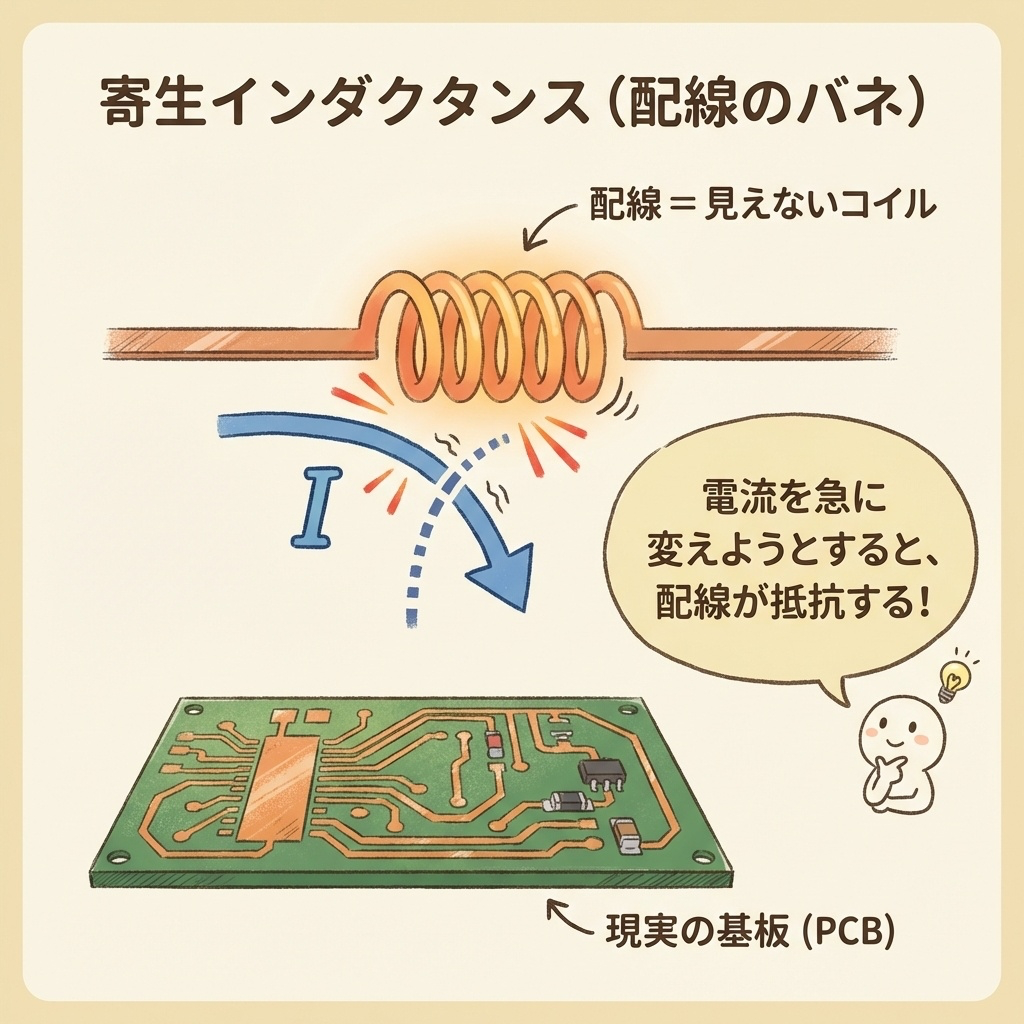
寄生インダクタンス|「配線に隠れたバネ」
配線はただの「線」ではない
回路図を描くとき、配線は「ただの線」として描きますよね。
しかし現実の配線には、目に見えないインダクタンス(L)が存在します。
これを寄生インダクタンス(Parasitic Inductance)と呼びます。
寄生インダクタンスを「バネ」でイメージする
寄生インダクタンスは、「配線に隠れたバネ」とイメージするとわかりやすいです。
バネは、急に押したり引いたりすると、強く反発しますよね?
でも、ゆっくり動かせば、スムーズに伸び縮みします。
寄生インダクタンスも同じです。
↓
反発(電圧スパイク)なし ✅
↓
電圧スパイク発生 ❌
どれくらいの寄生インダクタンスがあるのか?
寄生インダクタンスの大きさは、配線の長さ・太さ・形状によって決まります。
目安として、以下の値を覚えておきましょう。
| 配線の種類 | インダクタンスの目安 |
|---|---|
| リード線(1cm) | 約 10 nH |
| 基板パターン(1cm) | 約 5〜10 nH |
| 部品のリード | 約 2〜5 nH |
| 表面実装部品 | 約 0.5〜2 nH |
「たった10nH(ナノヘンリー)でしょ?」と思うかもしれません。
しかし、計算してみると…
L = 10 nH = 10 × 10-9 H
dI/dt = 10A を 10ns で遮断 = 10 / (10 × 10-9) = 109 A/s
V = L × dI/dt = 10 × 10-9 × 109 = 10V
たった1cmの配線で、10Vものノイズが発生します!
パワエレ回路では、dI/dtが非常に大きい(電流の変化が非常に速い)ため、
わずかな寄生インダクタンスでも、大きなノイズになるのです。
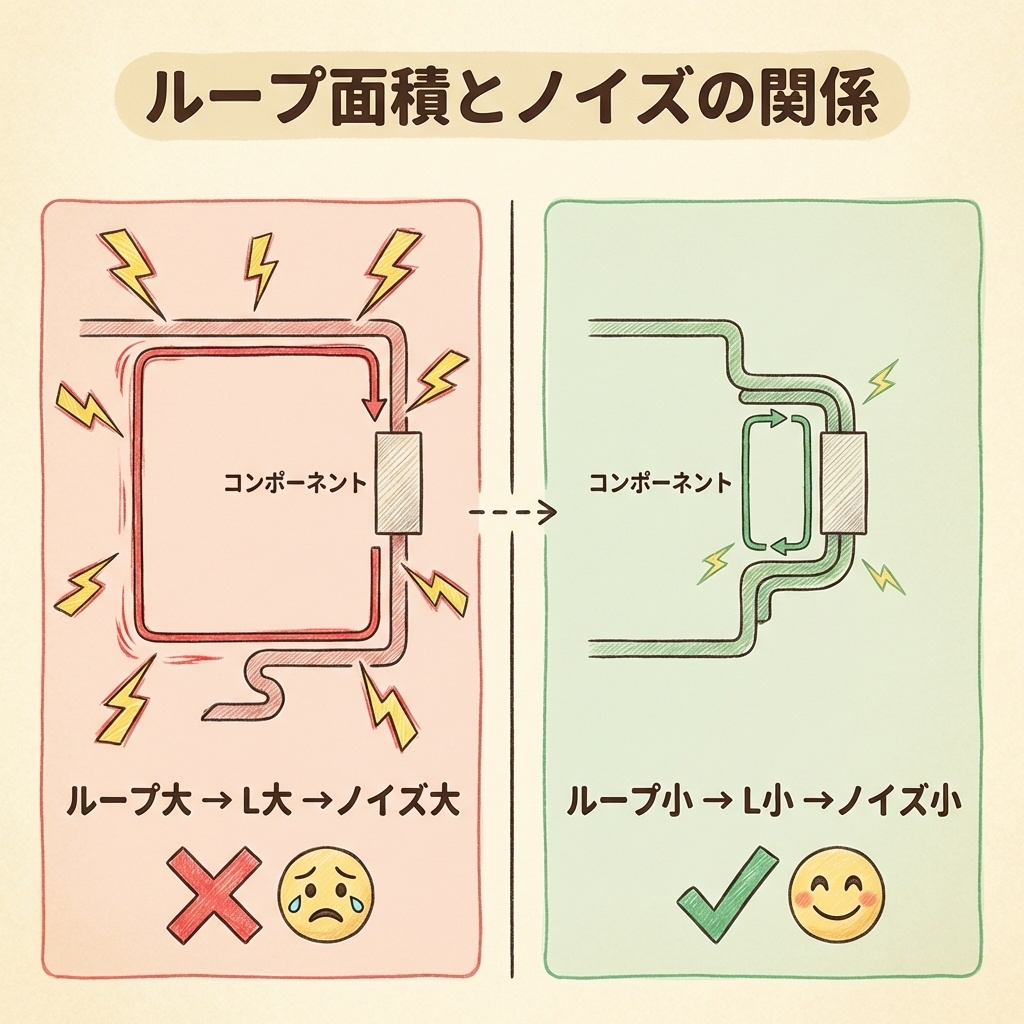
ループ面積とノイズの関係|「小さく、小さく」が鉄則
なぜ「ループ面積を小さく」と言われるのか?
パワエレ設計で必ず言われる「ループ面積を小さくしろ」というアドバイス。
これは、寄生インダクタンスを減らすことに直結しています。
配線のインダクタンスLは、ループの面積にほぼ比例します。
ループ面積 ∝ インダクタンスL ∝ ノイズV
ループ面積が2倍になれば、ノイズも約2倍になる!
ループ面積の比較イメージ
↓
L が大きい
↓
ノイズ大 ❌
↓
L が小さい
↓
ノイズ小 ✅
ループ面積を小さくする具体的な方法
パワエレ基板設計では、以下の方法でループ面積を小さくします。
| 対策 | 具体的な方法 |
|---|---|
| 部品を近づける | スイッチング素子、ダイオード、コンデンサをできるだけ近くに配置 |
| 配線を太く短く | 大電流が流れる配線は太く・短くする |
| 往復配線を近づける | 行きと帰りの配線を平行に、近くに配置(磁界が打ち消し合う) |
| ベタGNDを活用 | GND面を広く取り、リターンパスを最短にする |
| スナバコンデンサ | スイッチング素子の直近にコンデンサを配置し、ノイズを吸収 |
まとめ|スイッチングノイズを抑えるための3つの視点
この記事では、スイッチングノイズの発生メカニズムを「ウォーターハンマー」のイメージで解説しました。
- スイッチングノイズ = 電流を急に止めたときの「電気のウォーターハンマー」
- V = L × dI/dt = 慣性(L)× 急変度(dI/dt)でノイズが決まる
- 寄生インダクタンス = 配線に隠れた「目に見えないバネ」
- ループ面積 ∝ L ∝ ノイズ = ループを小さくすればノイズも減る
ノイズ対策の3つの視点
ノイズ対策は「後から」では手遅れになることが多いです。
設計の初期段階から「ループ面積を小さく」を意識して、部品配置・配線を行いましょう。
スイッチングノイズは「なぜ出るのか」を理解すれば、対策の方向性が見えてきます。
ぜひこの記事の内容を、実際の設計に活かしてください。
📚 次に読むべき記事
パワエレ基板設計の基本的な考え方を学ぶ
ノイズ対策にも関わる層構成の選び方
パワエレの基礎から理解を深める