💭 こんな悩みはありませんか?
- 「比例推移」って何?難しそう...
- T ∝ s とか I₂ ∝ s とか、何が何に比例するの?
- 計算問題で使い方がわからない
✅ この記事の結論
比例推移とは「滑りが小さい範囲では、いろんな量が滑りに比例する」という超便利な法則です。これを使えば、複雑な計算が一瞬で解けます!
📚 誘導機シリーズ(全8回)
2-1 原理 → 2-2 滑り → 2-3 比例推移 → 2-4 トルクと出力 → 2-5 等価回路 → 2-6 始動法 → 2-7 速度制御 → 2-8 単相誘導電動機
🔙 前回のおさらい
滑り s は「回転磁界にどれだけ遅れているか」を表す値でしたね。通常運転では s = 0.02〜0.05(2〜5%) という小さな値です。
目次
🎯 比例推移とは?|超シンプルな考え方
「比例推移」という難しそうな名前にビビらないでください。
要するに、「滑りが2倍になったら、〇〇も2倍になる」という単純な比例関係のことです。
身近な例で考えてみよう
お小遣いで考えてみましょう。
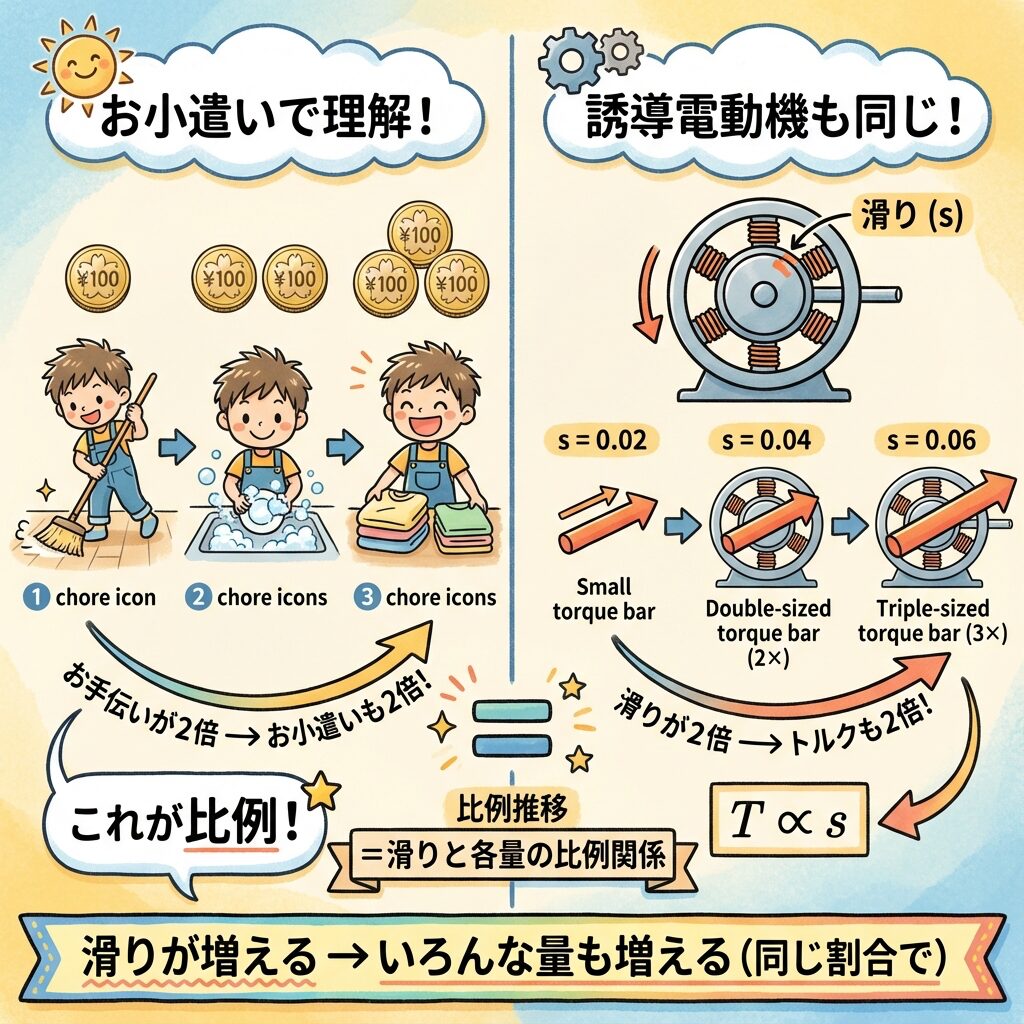
💰 お小遣いで理解する比例推移
「お手伝い1回につき100円もらえる」というルールがあるとします。
| お手伝い1回 → 100円 |
| お手伝い2回 → 200円(2倍) |
| お手伝い3回 → 300円(3倍) |
これが「比例」です。お手伝い回数が2倍になれば、お小遣いも2倍!
誘導電動機でも同じことが起きます。滑りが2倍になると、いくつかの量も2倍になるのです。
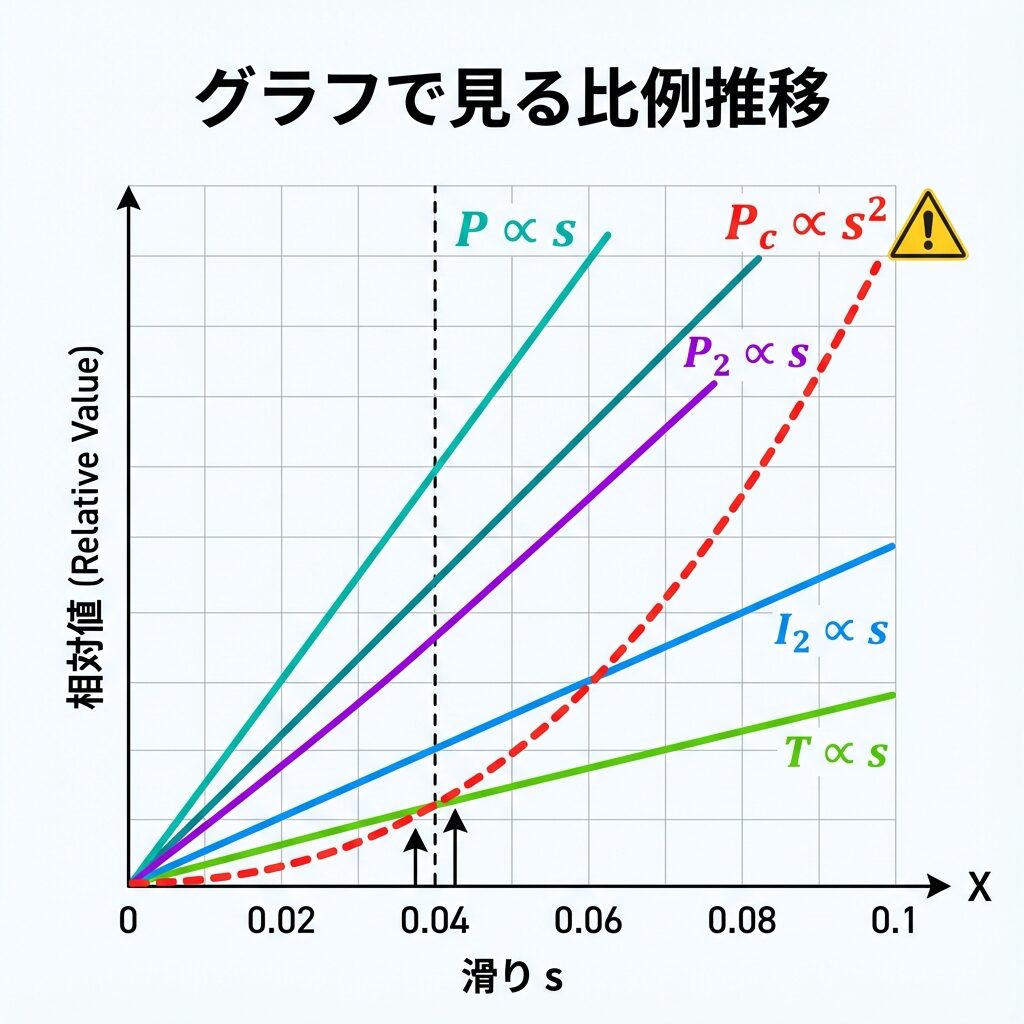
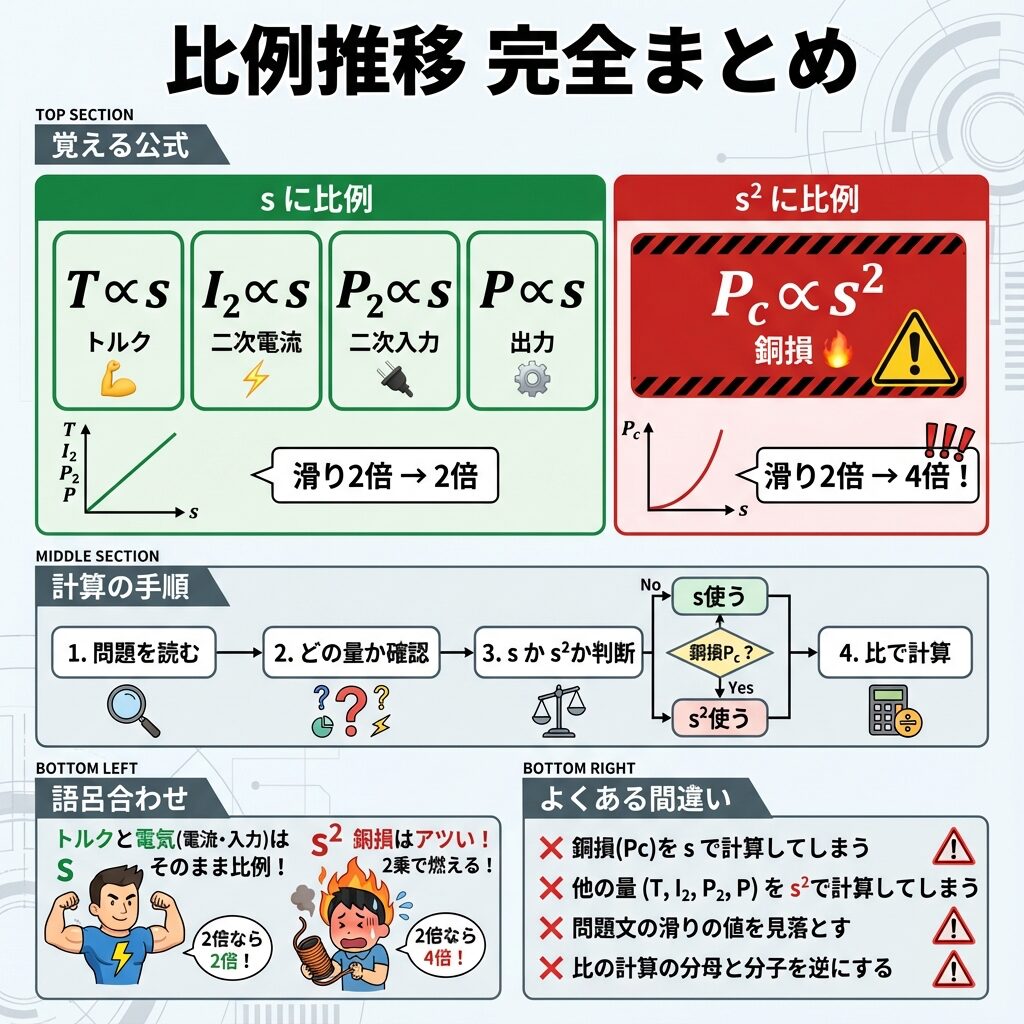
📊 滑りに比例する5つの量
滑りが小さい範囲(通常運転時)では、以下の5つが滑りに比例します。
| 記号 | 名前 | 比例関係 |
|---|---|---|
| T | トルク | T ∝ s |
| I₂ | 二次電流 | I₂ ∝ s |
| P₂ | 二次入力 | P₂ ∝ s |
| Pc | 二次銅損 | Pc ∝ s² |
| P | 出力(機械出力) | P ∝ s |
⚠️ 注意!銅損だけ「s²」に比例!
4つは「s」に比例しますが、銅損 Pc だけは「s²」に比例します。これは超頻出のひっかけポイント!
なぜ銅損だけ s² なの?
銅損は Pc = I₂²R で計算されます。
I₂ ∝ s なので、I₂² ∝ s² となります。だから銅損 Pc ∝ s² なのです!
💡 イメージで覚えよう
電流(I₂)が2倍になると...
銅損(Pc)は 2² = 4倍になる!
(電流の2乗に比例するから)
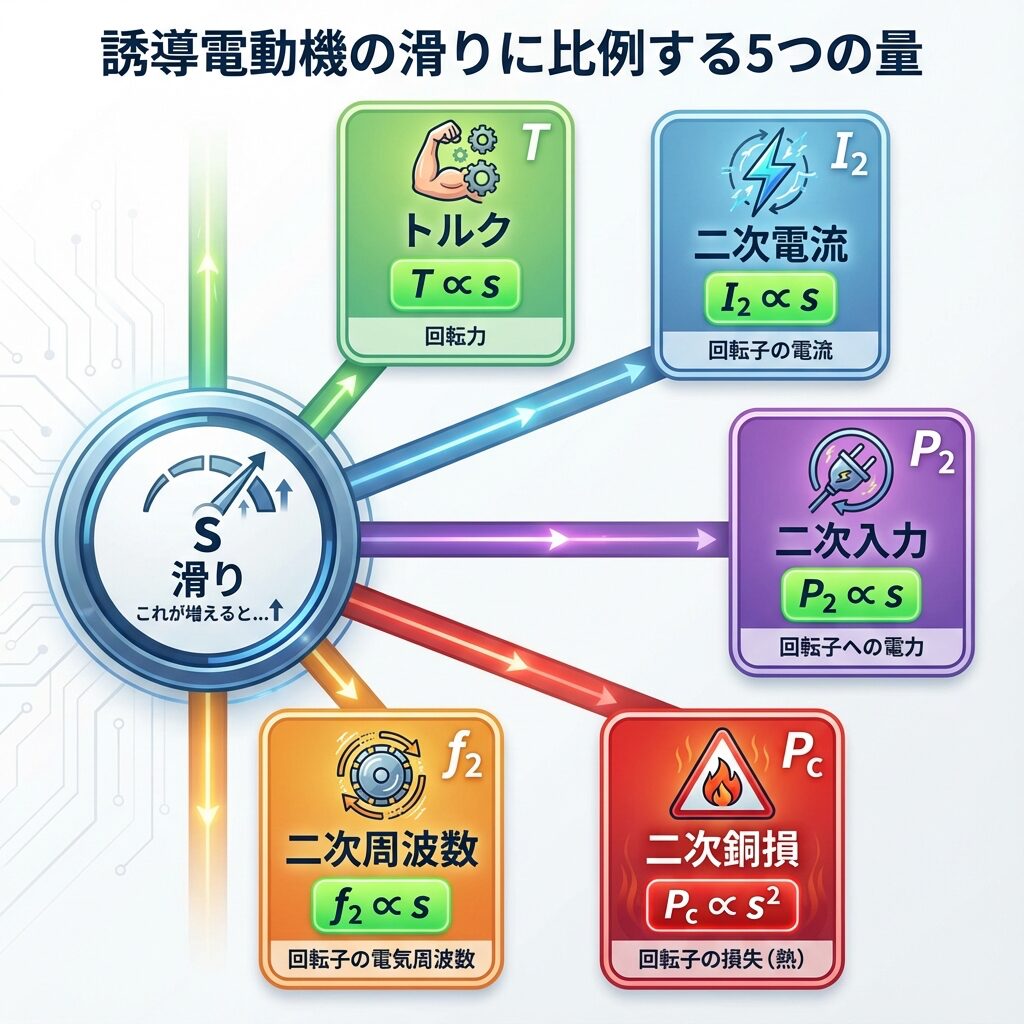
🔍 5つの量を詳しく理解しよう
それぞれの量が何を表すのか、イメージで理解しましょう。
① トルク T ∝ s
💪
トルク = 回転させる力
滑りが大きいほど、回転磁界との速度差が大きくなり、誘導される電流が増え、トルクも大きくなります。
② 二次電流 I₂ ∝ s
⚡
二次電流 = 回転子に流れる電流
滑りが大きいと、磁界の変化が激しくなり、誘導される電流も大きくなります。
③ 二次入力 P₂ ∝ s
🔌
二次入力 = 回転子に入る電力
固定子から回転子に伝わる電力。これが機械出力と銅損に分かれます。
④ 二次銅損 Pc ∝ s²(要注意!)
🔥
銅損 = 回転子の抵抗で熱になるロス
Pc = I₂²R なので、電流の2乗に比例。だからs²に比例!
⑤ 出力 P ∝ s
⚙️
出力 = 実際に機械を動かす力
二次入力から銅損を引いた残り。モーターが仕事をする力です。
🧮 比例推移の使い方|計算問題を解いてみよう
比例推移の真骨頂は計算問題が超簡単になること!
基本の考え方:比で解く!
比例関係があるということは、「比」で計算できるということです。
T₁ : T₂ = s₁ : s₂
(トルクの場合。他の量も同様)
つまり、滑りの比 = 各量の比 になります!
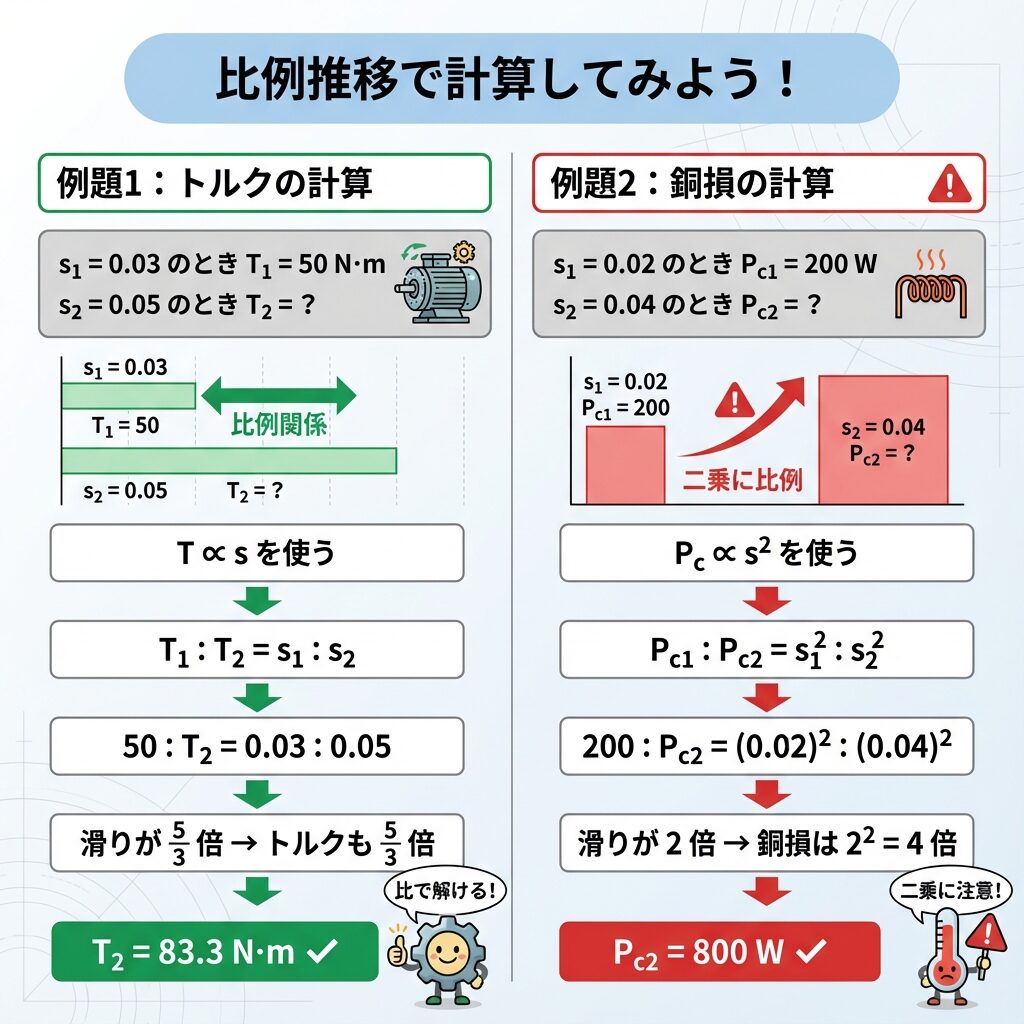
例題1:トルクの計算
📋 問題
ある誘導電動機が滑り s₁ = 0.03 で運転しているとき、トルクは T₁ = 50 N·m である。滑りが s₂ = 0.05 に増加したとき、トルク T₂ はいくらか?
✏️ 解答
Step 1:比例推移を使う
T ∝ s より、T₁ : T₂ = s₁ : s₂
Step 2:値を代入
50 : T₂ = 0.03 : 0.05
Step 3:内項の積 = 外項の積
0.03 × T₂ = 50 × 0.05
T₂ = 2.5 / 0.03
T₂ = 83.3 N·m
💡 もっと簡単な考え方
滑りが 0.03 → 0.05 に増えた = 5/3倍になった
だからトルクも 5/3倍 → 50 × 5/3 = 83.3 N·m
例題2:銅損の計算(s²に注意!)
📋 問題
滑り s₁ = 0.02 で運転しているとき、二次銅損は Pc₁ = 200 W である。滑りが s₂ = 0.04 に増加したとき、二次銅損 Pc₂ はいくらか?
⚠️ 注意!銅損は s² に比例!
銅損は Pc ∝ s² なので、滑りの「2乗」の比になります!
✏️ 解答
Step 1:比例推移を使う(s²に注意!)
Pc ∝ s² より、Pc₁ : Pc₂ = s₁² : s₂²
Step 2:値を代入
200 : Pc₂ = 0.02² : 0.04²
200 : Pc₂ = 0.0004 : 0.0016
Step 3:計算
滑りが2倍 → 銅損は 2² = 4倍
Pc₂ = 200 × 4 = 800 W
🎯 試験でのひっかけポイント!
滑りが2倍になったとき...
| トルク T | → 2倍 |
| 二次電流 I₂ | → 2倍 |
| 二次入力 P₂ | → 2倍 |
| 銅損 Pc | → 4倍(2²倍)⚠️ |
| 出力 P | → 2倍 |
⚠️ 比例推移が使える条件
比例推移は万能ではありません。滑りが小さい範囲でのみ成り立ちます。
使える条件
✅ 比例推移が使える場合
- 通常運転時(s = 0.02〜0.05程度)
- 負荷が変化したときの計算
- 電圧が一定の条件
❌ 比例推移が使えない場合
- 始動時(s = 1)のような大きな滑り
- 最大トルク付近の領域
- 電圧が変化する場合
なぜ「小さい範囲」限定なの?
実は、トルクと滑りの関係は完全な直線ではなく、曲線(トルク-滑り曲線)です。
しかし、滑りが小さい範囲では曲線が直線に近いので、比例として扱えるのです。
💡 イメージ:地球は丸いけど、家の周りだけ見れば「平ら」として扱えるのと同じ!
🧠 覚え方のコツ
🎵 語呂合わせ:「TIP₂P、銅だけ2乗」
T(トルク)・I₂(二次電流)・P₂(二次入力)・P(出力)→ s に比例
銅(Pc)だけ2乗 → s² に比例
📝 まとめ
🏆 これだけ覚えて帰ろう!
| 比例推移とは | 滑りが小さい範囲で成り立つ比例関係 |
| s に比例 | T, I₂, P₂, P |
| s² に比例 | Pc(銅損)⚠️ |
| 計算方法 | 比で計算! T₁:T₂ = s₁:s₂ |
📚 誘導機シリーズ 全記事一覧
| 2-1. 三相誘導電動機の原理 🔗 | 2-4. トルクと出力の関係 🔗 |
| 2-2. 滑り(すべり)🔗 | 2-5. 等価回路 🔗 |
| 2-3. 比例推移 🔗 | 2-6. 始動法 🔗 |
| 2-7. 速度制御法 🔗 | 2-8. 単相誘導電動機 🔗 |
2-2. 滑り(すべり)|基礎から理解する →