💭 こんな悩みはありませんか?
- P₂とかPとかPcとか、記号が多すぎて混乱する...
- 1:(1-s):s って何?どう使うの?
- トルクと出力の関係がイメージできない
✅ この記事の結論
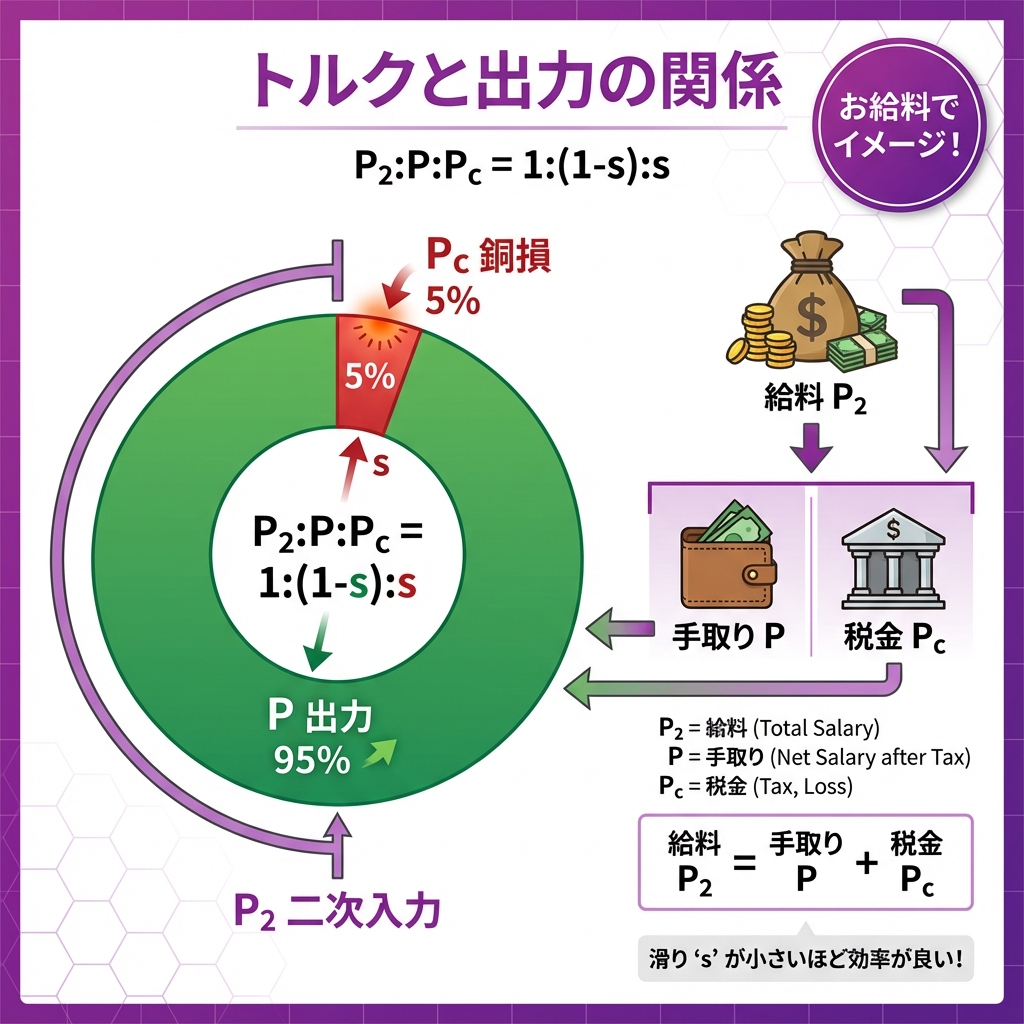
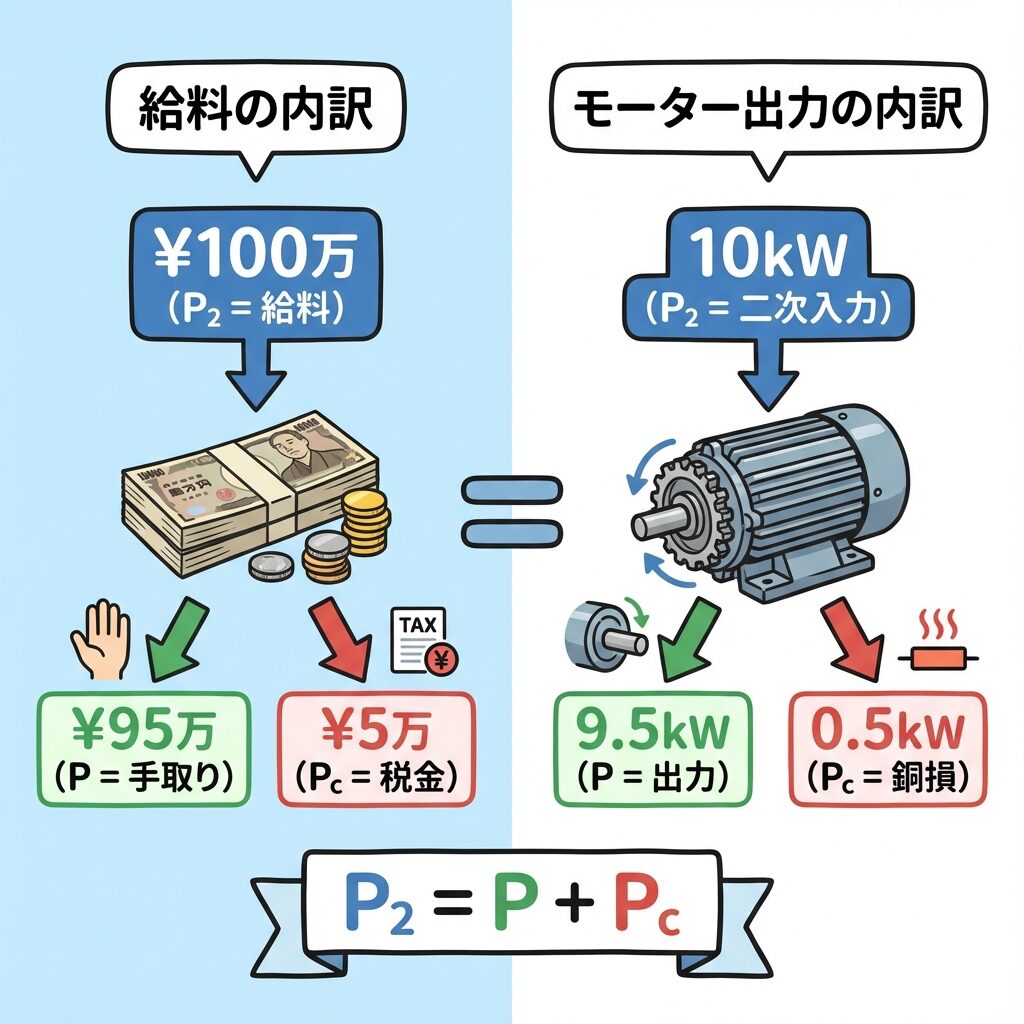
二次入力P₂は「お給料」、出力Pは「手取り」、銅損Pcは「税金」と考えれば一発で理解できます!
📚 誘導機シリーズ(全8回)
2-1 原理 → 2-2 滑り → 2-3 比例推移 → 2-4 トルクと出力 → 2-5 等価回路 → 2-6 始動法 → 2-7 速度制御 → 2-8 単相誘導電動機
目次
💰 お給料で理解する!P₂・P・Pcの関係
まず、3つの記号の意味をお給料に例えて理解しましょう。
お給料のたとえ
💵
P₂(二次入力)
= お給料(総支給額)
会社からもらう金額
👛
P(出力)
= 手取り
実際に使えるお金
🏛️
Pc(銅損)
= 税金
引かれてしまうロス
つまり、こういうことです。
P₂ = P + Pc
お給料 = 手取り + 税金
お給料から税金を引いたら手取りになる。当たり前ですよね!
誘導電動機も同じで、二次入力から銅損(熱ロス)を引いたら出力(実際の仕事)になるのです。
⚖️ 黄金比!P₂:P:Pc = 1:(1-s):s
ここからが超重要!3つの量の比を覚えましょう。
魔法の比を覚えよう!
🌟 超重要公式 🌟
P₂ : P : Pc = 1 : (1-s) : s
二次入力 : 出力 : 銅損 = 1 : (1-滑り) : 滑り
この比を使えば、どれか1つがわかれば残り2つが計算できます!
具体例で理解しよう
滑り s = 0.05(5%)の場合を考えてみましょう。
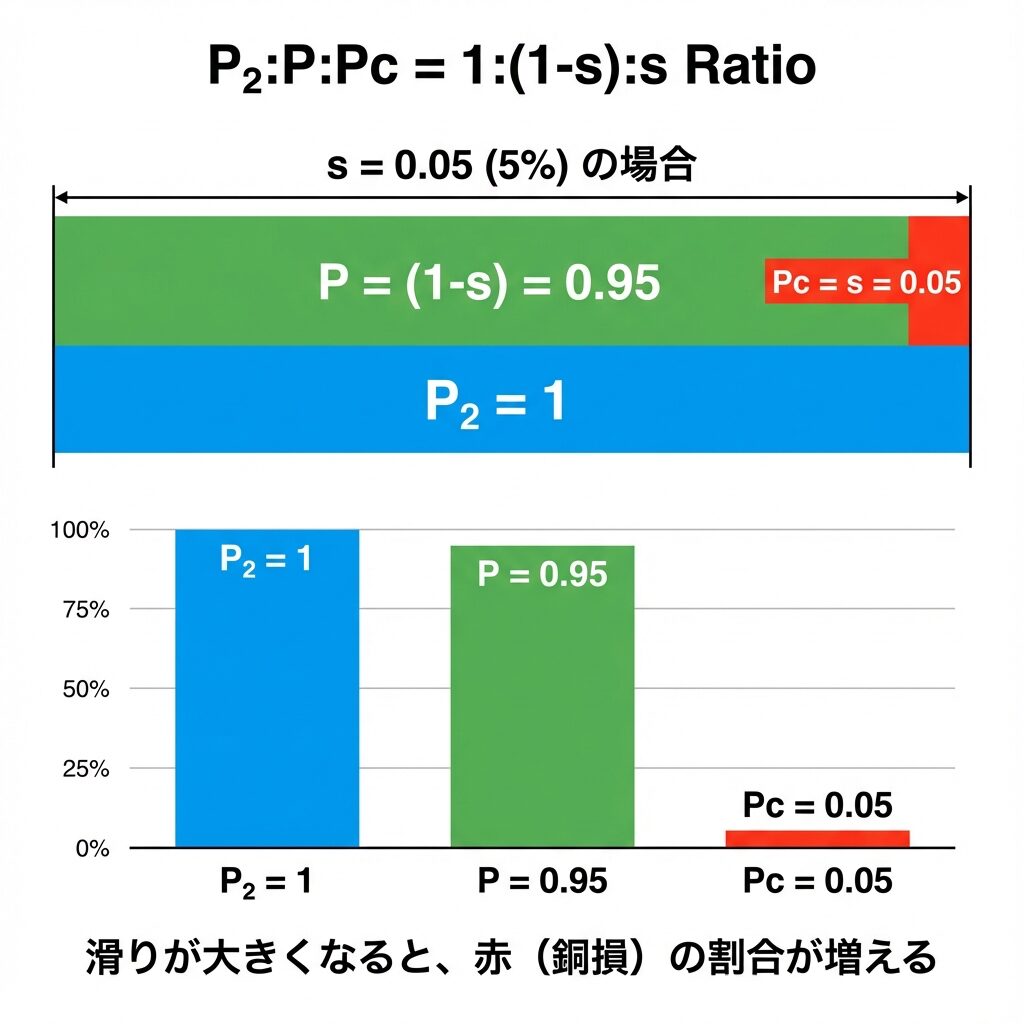
📝 s = 0.05 のとき
P₂ : P : Pc = 1 : (1-0.05) : 0.05
P₂ : P : Pc = 1 : 0.95 : 0.05
→ 二次入力の95%が出力、5%が銅損(熱ロス)になる!
💰 お給料でイメージ!
お給料が100万円で、税率が5%だとすると...
| P₂(お給料) | 100万円 | (100%) |
| P(手取り) | 95万円 | (95% = 1-s) |
| Pc(税金) | 5万円 | (5% = s) |
滑り = 税率 と考えると覚えやすい!
なぜこの比になるの?
実は、この比は速度の比から来ています。
| 量 | 比 | 速度との関係 |
|---|---|---|
| P₂(二次入力) | 1 | 同期速度 Ns に対応 |
| P(出力) | 1-s | 回転速度 N に対応 |
| Pc(銅損) | s | 速度差 Ns-N に対応 |
🔄 変形公式をマスターしよう
比の公式から、いろんな計算式が導けます。
出力を求める公式
P = P₂(1 - s)
出力 = 二次入力 ×(1 - 滑り)
💡 イメージ:手取り = お給料 ×(1 - 税率)
銅損を求める公式
Pc = P₂ × s = P × s/(1-s)
銅損 = 二次入力 × 滑り
トルクと出力の関係
ここでもう一つ重要な公式があります。
P = T × ω [W]
| P | 出力 [W] |
| T | トルク [N·m] |
| ω | 角速度 [rad/s] = 2πN/60 |
🚴 自転車でイメージ!
出力 P = どれだけ仕事をしているか
トルク T = ペダルを踏む力
角速度 ω = ペダルの回転速度
強く踏んで(T大)、速く回す(ω大)ほど、たくさん仕事(P大)ができる!
公式まとめ
| 求めたいもの | 公式 |
|---|---|
| 出力 P | P = P₂(1-s) = T×ω |
| 銅損 Pc | Pc = P₂×s |
| 二次入力 P₂ | P₂ = P + Pc = P/(1-s) |
| トルク T | T = P/ω = P₂/ωs |
📝 計算例|実際に解いてみよう!
例題1:出力と銅損を求める
📋 問題
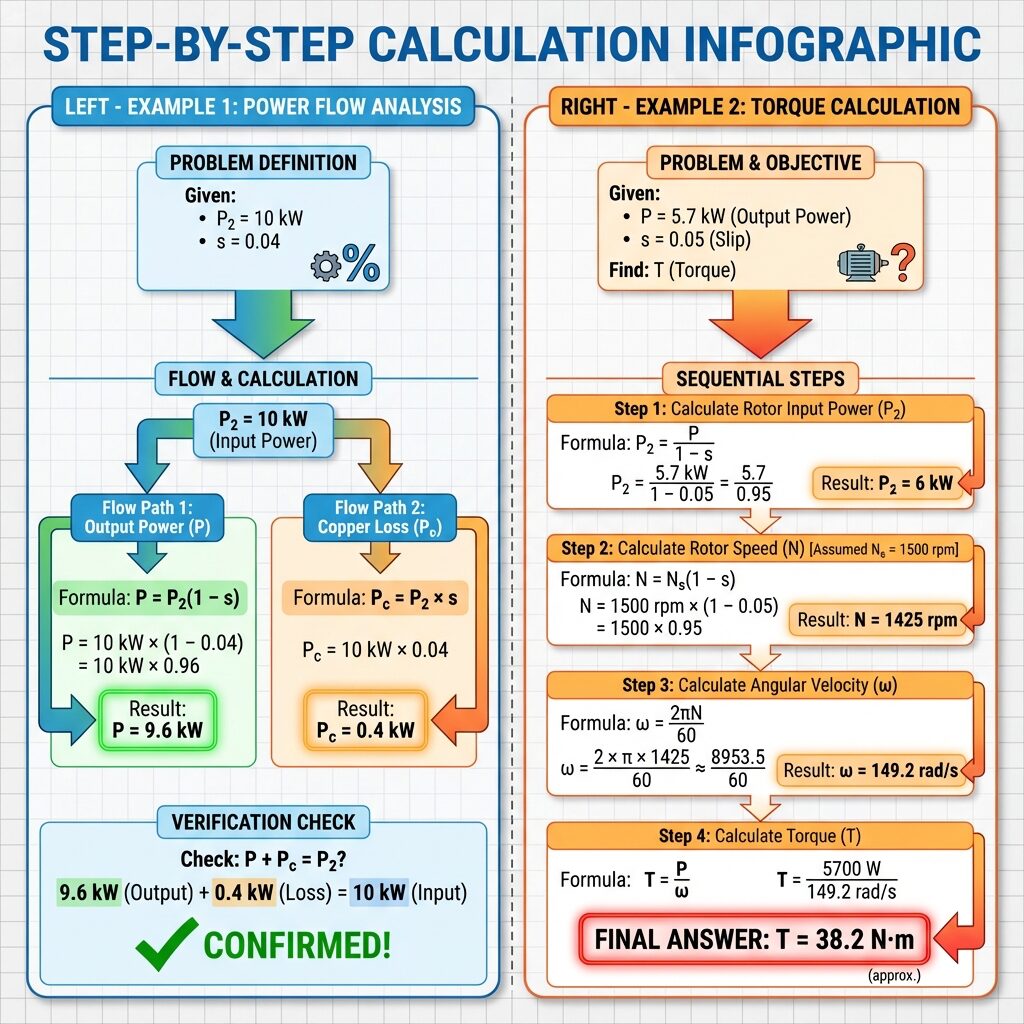
三相誘導電動機の二次入力が P₂ = 10 kW、滑りが s = 0.04(4%)のとき、出力 P と二次銅損 Pc を求めよ。
✏️ 解答
Step 1:比を確認
P₂ : P : Pc = 1 : (1-s) : s = 1 : 0.96 : 0.04
Step 2:出力 P を計算
P = P₂ × (1-s) = 10 × 0.96 = 9.6 kW
Step 3:銅損 Pc を計算
Pc = P₂ × s = 10 × 0.04 = 0.4 kW(400 W)
💡 検算:P + Pc = 9.6 + 0.4 = 10 kW = P₂ ✓
例題2:二次入力とトルクを求める
📋 問題
4極、50Hzの三相誘導電動機が、滑り s = 0.05 で運転し、出力が P = 5.7 kW である。二次入力 P₂ とトルク T を求めよ。
✏️ 解答
Step 1:二次入力 P₂ を計算
P = P₂(1-s) より
P₂ = P / (1-s) = 5.7 / 0.95 = 6 kW
Step 2:回転速度 N を計算
Ns = 120f/p = 120×50/4 = 1500 min⁻¹
N = Ns(1-s) = 1500×0.95 = 1425 min⁻¹
Step 3:角速度 ω を計算
ω = 2πN/60 = 2π×1425/60 = 149.2 rad/s
Step 4:トルク T を計算
T = P/ω = 5700/149.2 = 38.2 N·m
2-3. 比例推移|T ∝ s の関係を復習する →
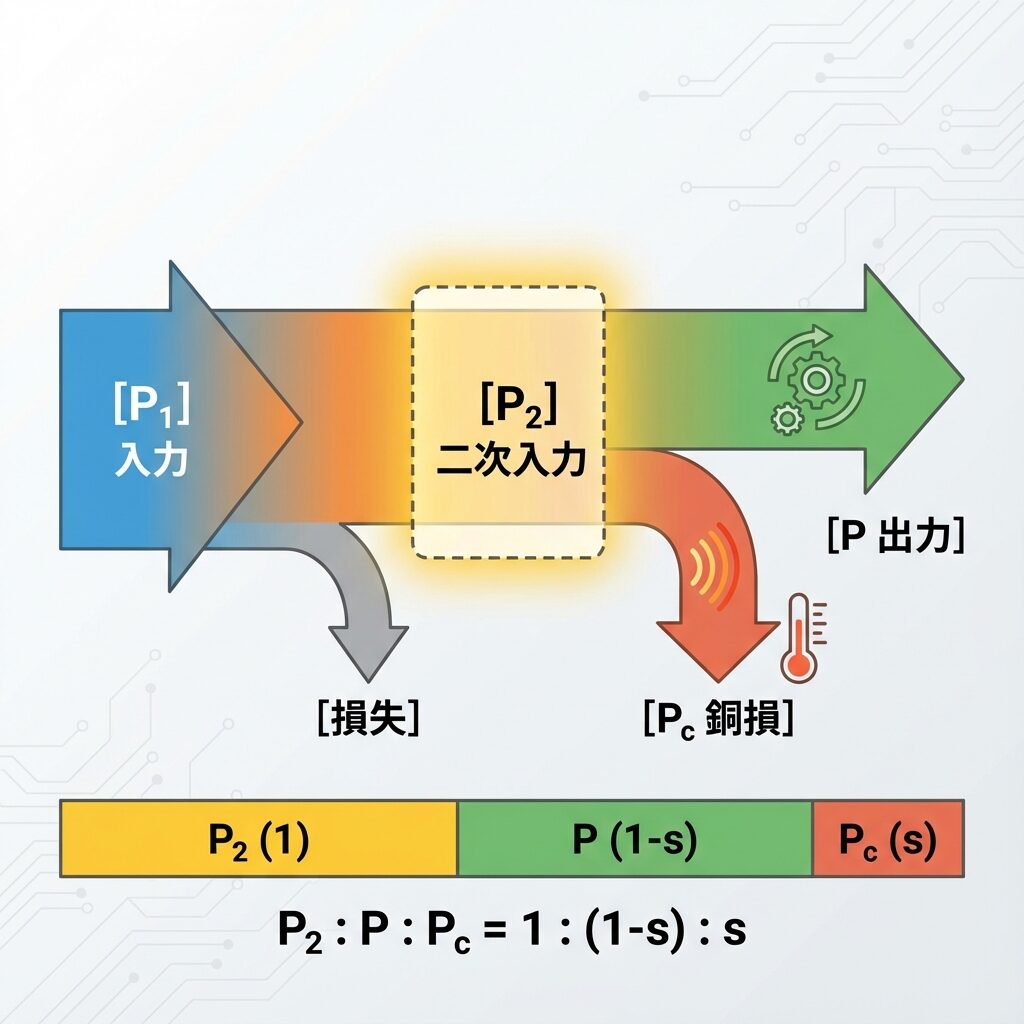
⚡ エネルギーの流れを理解しよう
最後に、誘導電動機の中でエネルギーがどう流れるかを見てみましょう。
エネルギーフロー図
P₁
一次入力
一次銅損
鉄損
P₂
二次入力
Pc
二次銅損
P
機械出力
電気エネルギーが段階的に機械エネルギーに変換される
💡 ポイント:今回の記事で扱ったのは、P₂(二次入力)から先の部分です!
🧠 覚え方のコツ
🎵 語呂合わせ:「給料から税金引いたら手取り」
| P₂(二次入力) | = | 給料(100%) |
| Pc(銅損) | = | 税金(s%) |
| P(出力) | = | 手取り((1-s)%) |
📝 まとめ
🏆 これだけ覚えて帰ろう!
| 基本の関係 | P₂ = P + Pc |
| 黄金比 | P₂ : P : Pc = 1 : (1-s) : s |
| 出力の公式 | P = P₂(1-s) = T×ω |
| イメージ | 給料 = 手取り + 税金 |
📚 誘導機シリーズ 全記事一覧
| 2-1. 三相誘導電動機の原理 🔗 | 2-4. トルクと出力の関係 🔗 |
| 2-2. 滑り(すべり)🔗 | 2-5. 等価回路 🔗 |
| 2-3. 比例推移 🔗 | 2-6. 始動法 🔗 |
| 2-7. 速度制御法 🔗 | 2-8. 単相誘導電動機 🔗 |
機械科目の全体像|学習ロードマップ →