📘 この記事でわかること
- 検定・推定を体系的に学ぶ最適な順番
- 「計量値」と「計数値」の使い分け
- どの検定を使うかが一目でわかるフローチャート
- QC検定・統計検定の頻出範囲と優先度
- 全28記事の学習ロードマップ
「検定って種類が多すぎて、どれを使えばいいかわからない…」
「t検定とZ検定の違いは?F検定とカイ二乗検定は何が違うの?」
「勉強しても、実際の問題で手が止まってしまう…」
統計学の「検定・推定」は、多くの人がつまずくポイントです。その理由は明確で、「全体像が見えないまま、個別の検定を学んでいる」からです。
検定・推定には「地図」が必要です。どこから始めて、どこに向かうのか。その道筋が見えれば、迷うことなく学習を進められます。
💡 結論:3つのSTEPで完全攻略できる!
検定・推定は、①基礎概念 → ②計量値の検定 → ③計数値の検定の順に学べば、確実にマスターできます。この記事では、全28記事を最適な順番で紹介し、あなたの学習を完全サポートします。
目次
検定・推定の全体像|まずは「地図」を手に入れよう
検定・推定を学ぶ前に、まずは全体像を把握しましょう。下の図が、このロードマップの「地図」です。
🗺️ 検定・推定の学習マップ
STEP 1:基礎概念(6記事)
帰無仮説・P値・有意水準・第1種/第2種の過誤・点推定/区間推定
STEP 2:計量値の検定・推定(13記事)
分散の検定(カイ二乗・F検定)→ 平均の検定(Z・t検定)→ 区間推定
STEP 3:計数値の検定・推定(9記事)
母比率の検定 → 母不適合数の検定 → 区間推定
「計量値」と「計数値」の違い
検定・推定を学ぶ上で、最も重要な分類が「計量値」と「計数値」の違いです。
| 種類 | 特徴 | 例 |
|---|---|---|
| 計量値 | 連続的な数値データ 「測定」して得られる |
長さ、重さ、時間、温度、強度など |
| 計数値 | 離散的な数値データ 「数えて」得られる |
不良品数、欠点数、合格/不合格の割合など |
💡 覚え方のコツ
計量値=「はかる」(測る)→ 測定器を使う → 連続値
計数値=「かぞえる」(数える)→ 1個、2個と数える → 離散値
なぜこの順番で学ぶのか?
このロードマップは、「前提知識 → 応用」の順に設計されています。
① 基礎概念が先
「帰無仮説」「P値」「有意水準」を理解していないと、どの検定を学んでも意味がわかりません。まずは土台を固めます。
② 計量値が先、計数値が後
計量値の検定(t検定など)は、正規分布を前提としているため、理論が理解しやすいです。計数値の検定は、二項分布やポアソン分布の知識が必要なため、後に回します。
③ 分散 → 平均の順
2つの平均を比較する「t検定」を行う前に、「F検定」で分散が等しいか確認する必要があります。そのため、分散の検定を先に学びます。
▼ 下の図は、検定・推定の全体像と学習の流れを示しています
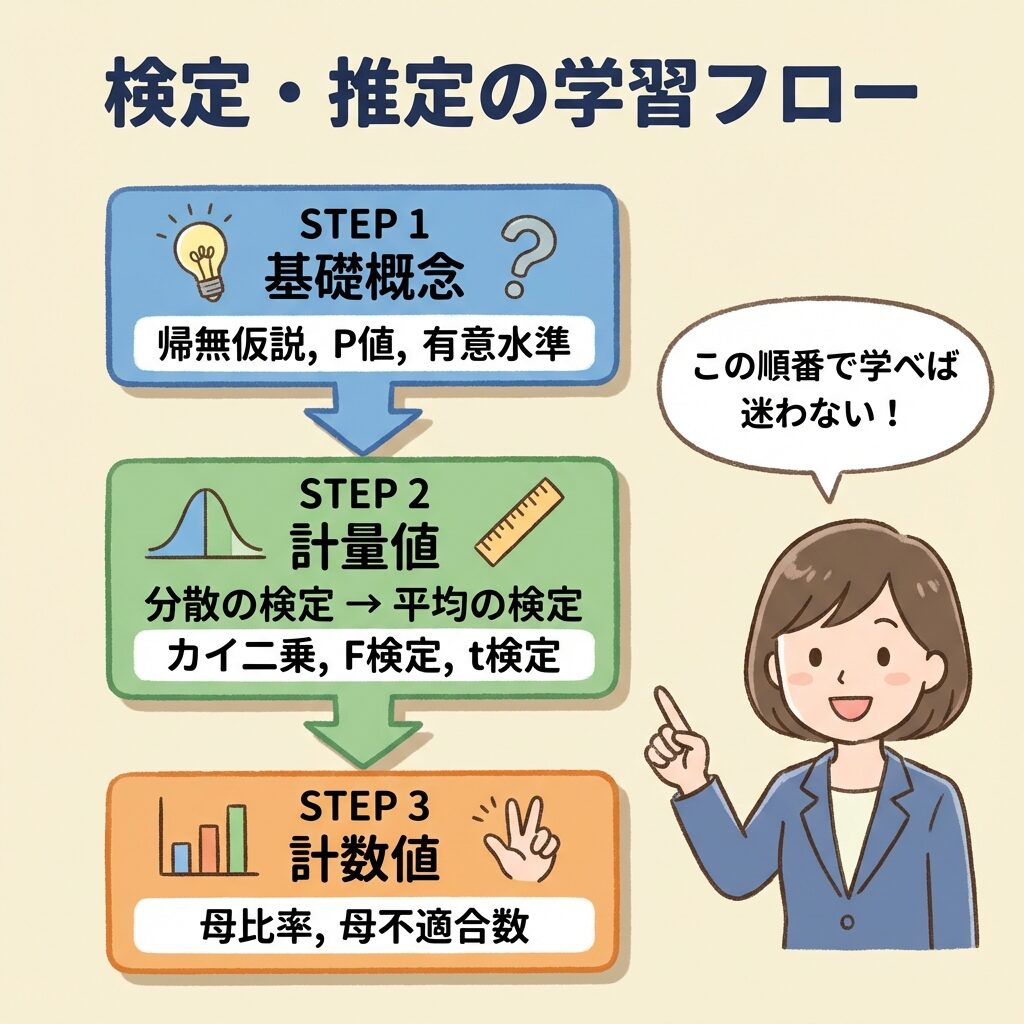
【STEP 1】基礎概念|まずはここから(6記事)
検定・推定を学ぶ最初のステップは、「検定とは何か?」を理解することです。この6記事を順番に読めば、検定の基本的な考え方が身につきます。
🎯 STEP 1の学習目標
- 「検定」と「推定」の違いがわかる
- 「帰無仮説」と「対立仮説」の意味がわかる
- 「P値」と「有意水準」の関係がわかる
- 「第1種の過誤」と「第2種の過誤」の違いがわかる
- どの検定を使うかフローチャートで選べる
STEP 1の記事一覧(推奨順)
【超入門】「統計的仮説検定」と「推定」って何?数式なしでイメージだけで理解する
検定と推定の全体像を、数式なしでイメージで理解します。「なぜ検定が必要なのか?」という根本的な疑問に答える入門記事です。
⏱ 読了目安:10分 | 🎯 重要度:★★★★★
【統計学】「帰無仮説」棄却のロジック|なぜ「差がある」と言わずに「差がないとは言えない」という捻くれた言い方をするのか?
検定の最重要概念「帰無仮説」と「対立仮説」を解説。なぜ回りくどい言い方をするのか、その理由がスッキリわかります。
⏱ 読了目安:12分 | 🎯 重要度:★★★★★
【統計学】P値と有意水準(α)|「5%の奇跡」が起きたら、それは偶然じゃないと疑う
検定の結論を出すための「P値」と「有意水準α」の関係を解説。「5%」という数字の意味が腹落ちします。
⏱ 読了目安:10分 | 🎯 重要度:★★★★★
【統計学】第1種の過誤(生産者危険)と第2種の過誤(消費者危険)|あわてんぼうとぼんやり者、どっちが罪深い?
検定で起こりうる2種類の間違い「αエラー」と「βエラー」を、わかりやすい例えで解説します。
⏱ 読了目安:10分 | 🎯 重要度:★★★★☆
【統計学】点推定と区間推定の違いは?「言い切る」危うさと「幅を持たせる」誠実さ
推定の2つの方法「点推定」と「区間推定」の違いを解説。なぜ「95%信頼区間」という幅を持たせるのか、その理由がわかります。
⏱ 読了目安:8分 | 🎯 重要度:★★★★☆
【保存版】統計検定の選び方フローチャート|計量・計数、対応あり・なしで迷わない最強の地図
「どの検定を使えばいいか?」を一発で判断できるフローチャート。この記事をブックマークしておけば、もう迷いません。
⏱ 読了目安:15分 | 🎯 重要度:★★★★★ | 🔖 ブックマーク推奨
✅ STEP 1 完了チェック
以下の質問に答えられるようになったら、STEP 2へ進みましょう!
- 「帰無仮説」とは何か説明できる
- 「P値 < 0.05」の意味がわかる
- 「第1種の過誤」と「第2種の過誤」の違いがわかる
- フローチャートを見て、どの検定を使うか選べる
▼ 下の図は、STEP 1で学ぶ概念の関係図を示しています
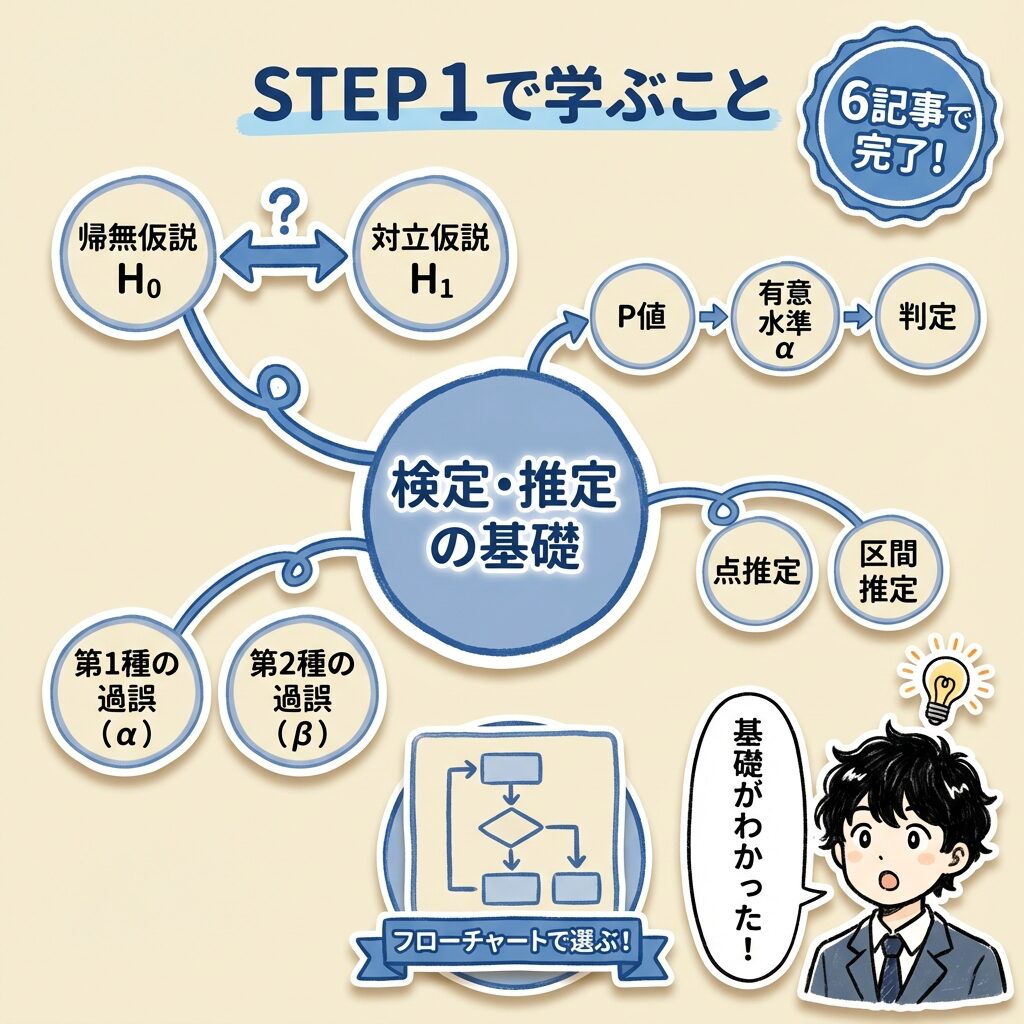
【STEP 2】計量値の検定・推定|数値データを扱う(13記事)
基礎概念を理解したら、次は「計量値」の検定・推定を学びます。計量値とは、長さ・重さ・時間などの「測定」して得られる連続的な数値データです。
STEP 2は、さらに「分散に関する検定」と「平均に関する検定」の2つに分かれます。
🎯 STEP 2の学習目標
- カイ二乗検定で「1つのデータのバラつき」を検証できる
- F検定で「2つのデータのバラつき」を比較できる
- t検定で「平均の差」を検証できる
- 「対応あり」と「対応なし」の使い分けがわかる
- 母平均・母分散の区間推定ができる
STEP 2-1:分散に関する検定・推定(5記事)
まずは「分散(バラつき)」に関する検定から始めます。なぜ分散を先に学ぶのか?それは、平均の検定(t検定)を行う前に、分散が等しいかどうかを確認する必要があるからです。
カイ二乗検定(母分散)「この機械、バラつき増えてない?」を1つのデータで検証する手順
1つの標本から母分散を検定する「カイ二乗検定」を解説。工場の機械精度を確認する実務的な例で学びます。
⏱ 読了目安:12分 | 🎯 重要度:★★★★☆
カイ二乗分布の非対称性|なぜ「上側」と「下側」で値が違うのか?バラつき検定の罠
カイ二乗分布は左右非対称。両側検定の際に「上側」と「下側」で異なる値を使う理由を図解します。
⏱ 読了目安:10分 | 🎯 重要度:★★★☆☆
母分散の区間推定|バラつきはどの範囲に収まる?カイ二乗分布で「最悪のケース」を予測する
母分散の95%信頼区間の求め方を解説。品質管理で「最悪でもこの範囲」と予測するために必要です。
⏱ 読了目安:10分 | 🎯 重要度:★★★☆☆
F検定(等分散の検定)「A機とB機、精度が良いのはどっち?」2つのバラつきを比較する
2つの標本の分散を比較する「F検定」を解説。t検定を行う前に、等分散かどうかを確認するために必須の検定です。
⏱ 読了目安:12分 | 🎯 重要度:★★★★★
F分布のイメージ|なぜ分散は「引き算」ではなく「割り算」で比べるのか?
F分布の直感的なイメージを解説。なぜ分散比を使うのか、その理由がわかります。
⏱ 読了目安:8分 | 🎯 重要度:★★★☆☆
STEP 2-2:平均に関する検定・推定(8記事)
分散の検定を学んだら、次は「平均」に関する検定です。これが、実務で最も使われる検定です。
Z検定(母分散既知)|現実にはほぼ使わないが、基礎として学ぶべき「神様の検定」
母分散がわかっている場合のZ検定。実務では使いませんが、t検定を理解するための土台になります。
⏱ 読了目安:10分 | 🎯 重要度:★★★☆☆
t検定(母分散未知・一標本)「この部品の長さは規格通り?」実務で最も使う基本の検定
1つの標本から母平均を検定する「一標本t検定」。品質管理で規格値と比較する最も基本的な検定です。
⏱ 読了目安:15分 | 🎯 重要度:★★★★★
t分布と自由度|なぜデータが少ないと「合格基準」が厳しくなるのか?裾野の広がりの正体
t分布の形と自由度の関係を図解。データが少ないほど裾野が広がる理由がわかります。
⏱ 読了目安:10分 | 🎯 重要度:★★★★☆
t検定(2標本・等分散)「スチューデントのt検定」でAとBの差を証明する手順
2つの標本の平均を比較する「二標本t検定」。等分散を仮定した場合の計算方法を解説します。
⏱ 読了目安:15分 | 🎯 重要度:★★★★★
ウェルチのt検定(等分散なし)|F検定で「バラつきが違う」と出た後の救世主
F検定で等分散が棄却された場合に使う「ウェルチのt検定」。自由度の計算方法が特殊です。
⏱ 読了目安:12分 | 🎯 重要度:★★★★☆
対応のあるt検定「ダイエットで痩せた?」個人差を消して差を見抜く最強の手法
同じ対象のビフォー・アフターを比較する「対応のあるt検定」。個人差を打ち消して効果を検証できます。
⏱ 読了目安:12分 | 🎯 重要度:★★★★★
母平均の区間推定|「真の平均値はどこにある?」95%信頼区間の計算手順
母平均の95%信頼区間の求め方を解説。実験計画法の推定でも使う重要な技術です。
⏱ 読了目安:10分 | 🎯 重要度:★★★★☆
検出力(Power)の計算|「実験したけど差が出なかった」を防ぐためのサンプルサイズnの決め方
検定の「検出力」とサンプルサイズの関係を解説。実験前に必要なサンプル数を計算する方法です。
⏱ 読了目安:15分 | 🎯 重要度:★★★☆☆
✅ STEP 2 完了チェック
以下の質問に答えられるようになったら、STEP 3へ進みましょう!
- カイ二乗検定とF検定の違いがわかる
- 「対応あり」と「対応なし」のt検定を使い分けられる
- F検定 → t検定の流れがわかる
- 母平均の95%信頼区間を計算できる
▼ 下の図は、計量値の検定の使い分けフローを示しています
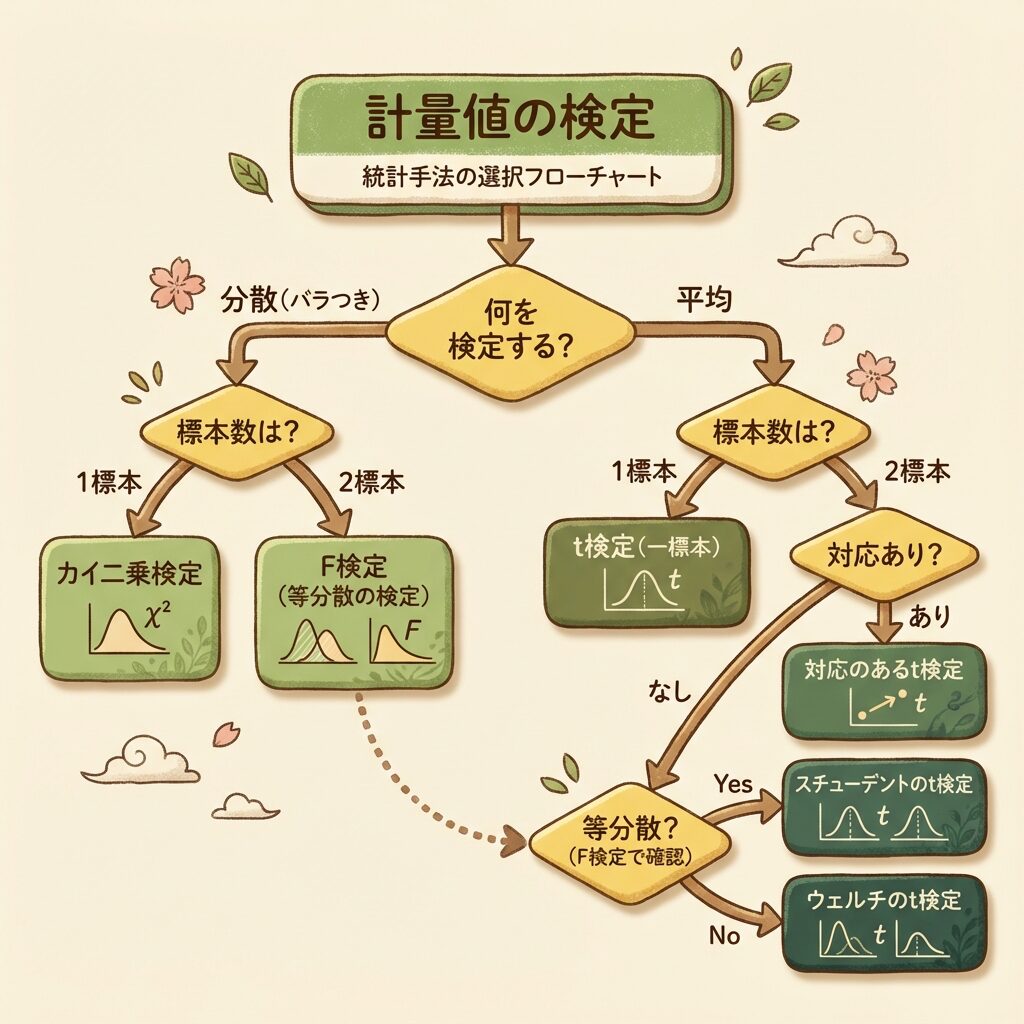
【STEP 3】計数値の検定・推定|割合・個数データを扱う(9記事)
最後のステップは「計数値」の検定・推定です。計数値とは、不良品数・欠点数・合格/不合格の割合など、「数えて」得られる離散的なデータです。
計数値の検定は、「母比率」と「母不適合数」の2つに分かれます。
🎯 STEP 3の学習目標
- 「母比率」と「母不適合数」の違いがわかる
- 不良率の改善効果を検証できる
- 2つの工場の不良率を比較できる
- サンプル数が少ない場合の検定方法がわかる
- 視聴率・支持率の「誤差±3%」の意味がわかる
STEP 3-1:母比率の検定・推定(6記事)
「母比率」とは、不良品の割合(不良率)や賛成者の割合(支持率)など、全体に対する特定カテゴリの割合のことです。
母比率の検定(大標本Z検定)|「不良率が5%から3%に減った」は改善か誤差か?
1つの標本から母比率を検定する方法。改善活動の効果を統計的に証明するための基本です。
⏱ 読了目安:12分 | 🎯 重要度:★★★★★
母比率の差の検定|「A工場とB工場の不良率に差はある?」2つの割合を比較する手順
2つの標本の比率を比較する検定。工場間・ライン間の品質比較に使います。
⏱ 読了目安:12分 | 🎯 重要度:★★★★☆
母比率の区間推定|テレビの視聴率や内閣支持率の「誤差±3%」はどう計算されているか?
母比率の95%信頼区間の求め方。ニュースで見る「誤差±3%」の計算根拠がわかります。
⏱ 読了目安:10分 | 🎯 重要度:★★★★☆
二項確率紙の使い方|計算なし!グラフに点を打つだけで検定・推定ができるアナログ技術
計算せずにグラフで検定・推定する「二項確率紙」の使い方。QC検定で出題されることがあります。
⏱ 読了目安:10分 | 🎯 重要度:★★★☆☆
フィッシャーの正確確率検定|サンプル数が少なすぎて「カイ二乗」が使えない時の最終兵器
サンプル数が少ない場合に使う「フィッシャーの正確確率検定」。2×2のクロス表で使います。
⏱ 読了目安:12分 | 🎯 重要度:★★★★☆
正確な信頼区間(F分布利用)|サンプル数が少ない時の「母比率」を厳密に計算する奥義
サンプル数が少ない場合の母比率の正確な信頼区間。F分布を使った厳密な計算方法です。
⏱ 読了目安:12分 | 🎯 重要度:★★★☆☆
STEP 3-2:母不適合数の検定・推定(3記事)
「母不適合数」とは、製品1個あたりの傷の数、布1m²あたりの汚点の数など、単位あたりの欠点数のことです。母比率との違いは、1つの製品に複数の欠点がありうることです。
母不適合数の検定(Z検定)|「不良率」と「欠点数」の違いは?ポアソン分布の近似
母不適合数の検定方法を解説。「不良率」と「欠点数」の違いを理解することが重要です。
⏱ 読了目安:12分 | 🎯 重要度:★★★★☆
母不適合数の差の検定とは?生産量が違う2つのラインを比較する方法
生産量(検査対象数)が異なる2つのラインの欠点数を比較する方法を解説します。
⏱ 読了目安:10分 | 🎯 重要度:★★★☆☆
母不適合数の区間推定とは?ポアソン分布なのに「カイ二乗」を使う理由
母不適合数の95%信頼区間の求め方。ポアソン分布とカイ二乗分布の関係がわかります。
⏱ 読了目安:10分 | 🎯 重要度:★★★☆☆
✅ STEP 3 完了チェック
以下の質問に答えられるようになったら、検定・推定をマスターしたと言えます!
- 「母比率」と「母不適合数」の違いがわかる
- 不良率の改善効果を検定できる
- サンプル数が少ない場合の対処法がわかる
- 視聴率の「誤差±3%」を自分で計算できる
▼ 下の図は、計数値の検定の使い分けを示しています

まとめ|検定・推定の学習ロードマップ
お疲れさまでした!この記事で紹介した28記事を順番に読めば、検定・推定を体系的にマスターできます。
📋 検定・推定の学習ロードマップ|全28記事
STEP 1:基礎概念(6記事)
検定と推定の全体像 → 帰無仮説 → P値・有意水準 → 第1種/第2種の過誤 → 点推定・区間推定 → フローチャート
STEP 2:計量値の検定・推定(13記事)
2-1 分散:カイ二乗検定 → F検定 → 母分散の区間推定
2-2 平均:Z検定 → t検定(1標本・2標本・対応あり・ウェルチ)→ 母平均の区間推定 → 検出力
STEP 3:計数値の検定・推定(9記事)
3-1 母比率:母比率の検定 → 母比率の差の検定 → 区間推定 → フィッシャー検定
3-2 母不適合数:母不適合数の検定 → 差の検定 → 区間推定
学習のコツ
① 順番を守る
基礎概念を飛ばして個別の検定を学ぶと、「なぜこの計算をするのか」がわからなくなります。必ずSTEP 1から始めましょう。
② フローチャートを何度も見る
「統計検定の選び方フローチャート」をブックマークして、問題を解くたびに確認しましょう。繰り返すうちに頭に入ります。
③ 手を動かす
記事を読むだけでなく、例題を自分で計算してみましょう。手を動かすことで、公式が体に染み込みます。
関連する学習ロードマップ
検定・推定を学んだら、以下のロードマップも併せて学習することで、統計学の全体像が見えてきます。
📚 実験計画法を学びたい方へ
【完全版】実験計画法の学習マップ|基礎から直交表・応用までを体系的に学ぶ
一元配置・二元配置・直交表など、実験計画法を体系的に学ぶロードマップです。検定・推定の知識が活きます。
💪
ここまで読んでくださった方へ
検定・推定は、最初は難しく感じるかもしれません。でも、この28記事を順番に読んで、手を動かして計算すれば、必ずマスターできます。
フローチャートを片手に、一歩ずつ進んでいきましょう。
あなたの統計学マスターへの道を、心から応援しています!
